
California State University, San Bernardino California State University, San Bernardino
CSUSB ScholarWorks CSUSB ScholarWorks
Electronic Theses, Projects, and Dissertations O<ce of Graduate Studies
3-2015
SYMMETRIC PRESENTATIONS AND RELATED TOPICS SYMMETRIC PRESENTATIONS AND RELATED TOPICS
Mashael U. Alharbi
California State University - San Bernardino
Follow this and additional works at: https://scholarworks.lib.csusb.edu/etd
Part of the Algebra Commons
Recommended Citation Recommended Citation
Alharbi, Mashael U., "SYMMETRIC PRESENTATIONS AND RELATED TOPICS" (2015).
Electronic Theses,
Projects, and Dissertations
. 128.
https://scholarworks.lib.csusb.edu/etd/128
This Thesis is brought to you for free and open access by the O<ce of Graduate Studies at CSUSB ScholarWorks. It
has been accepted for inclusion in Electronic Theses, Projects, and Dissertations by an authorized administrator of
CSUSB ScholarWorks. For more information, please contact [email protected].

Symmetric Presentations and Related Topics
A Thesis
Presented to the
Faculty of
California State University,
San Bernardino
In Partial Fulfillment
of the Requirements for the Degree
Master of Arts
in
Mathematics
by
Mashael Umar Alharbi
March 2015

Symmetric Presentations and Related Topics
A Thesis
Presented to the
Faculty of
California State University,
San Bernardino
by
Mashael Umar Alharbi
March 2015
Approved by:
Dr. Zahid Hasan, Committee Chair Date
Dr. J. Paul Vicknair, Committee Member
Dr. Joseph Chavez, Committee Member
Dr. Charles Stanton, Chair, Dr. Corey Dunn
Department of Mathematics Graduate Coordinator,
Department of Mathematics
iii
Abstract
In this thesis, we have presented our discovery of symmetric presentations of a number
of non-abelian simple groups, including the Mathieu group M
12
. We have given several
progenitors, permutation and monomial, including 2
∗
4
: (2
2
: 3), 2
∗
5
: D
10
, 2
∗
8
: ((4 ×
2) • D
4
), 3
∗
7
:
m
L
2
(7), 2
∗
6
: (Z
3
o Z
2
), and 2
∗
24
: (2
•
A
5
) and their homomorphic images
which include 4 • (M
12
: 2), the group of automorphisms of M
12
and several classical
groups. We have given the isomorphism type of each of the group mentioned in the
thesis. In each case, a proof of the isomorphism type is provided, either computer-based
or by hand. In addition, by hand constructions, using the technique of double coset
enumeration, are given for the groups L
2
(11) × 3, L
2
(11), P GL
2
(11), S
5
, (A
5
× A
5
) : 4,
A
7
, and 3
7
: L
2
(7).
iv
Acknowledgements
First, I thank God for everything in my life. I am so grateful to my advisor Dr. Zahid
Hassan for his guidance and advices that supported me throughout the period of writing
my thesis, a deep thank to him for his time and patience. I thank Dr. Joseph Chavez
and Dr. J. Paul Vicknair, for their approval to be the members on my committee and
guiding me through my graduate classes. I Also thank Dr. Corey Dunn and Dr. Charles
Stanton for everything they have done for me during my graduate studies. I Also thank
my classmate David Gomez for his information support through writing my thesis. I
deeply thank my parents, sisters, and brothers for the generous encouragement and
support. I am also deeply thankful to my dear husband for understanding and support
to make my dream becomes true. Last but not least, I am grateful to my wonderful
daughters whom encouraged me in my studies to be a good example for them.
v
Table of Contents
Abstract iii
Acknowledgements iv
List of Tables viii
List of Figures x
1 Introduction 1
2 Preliminaries 28
2.1 Group Theory Preliminaries . . . . . . . . . . . . . . . . . . . . . . . . . 28
2.2 Group Extension Preliminaries . . . . . . . . . . . . . . . . . . . . . . . 40
3 Double Coset Enumeration and Composition Factors 44
3.1 S
5
as a Homomorphic Image of 2
∗
4
: A
4
. . . . . . . . . . . . . . . . . . 45
3.1.1 The Construction of S
5
over A
4
. . . . . . . . . . . . . . . . . . . 45
3.1.2 Proof of the Isomorphism . . . . . . . . . . . . . . . . . . . . . . 50
3.2 L
2
(11) × 3 as a Homomorphic Image of 2
∗
4
: A
4
. . . . . . . . . . . . . . 51
3.2.1 The Construction of L
2
(11) × 3 over A
4
. . . . . . . . . . . . . . 51
3.2.2 Proof of the Isomorphism . . . . . . . . . . . . . . . . . . . . . . 58
3.3 Factor L
2
(11) × 3 by The Center of G . . . . . . . . . . . . . . . . . . . 59
3.4 L
2
(11) as a Homomorphic Image of 2
∗
4
: A
4
. . . . . . . . . . . . . . . . 60
3.4.1 The Construction of L
2
(11) over A
4
. . . . . . . . . . . . . . . . 60
3.5 P GL
2
(11) as a Homorphic Image of 2
∗
5
: D
10
. . . . . . . . . . . . . . . 63
3.5.1 The Construction of P GL
2
(11) over D
10
. . . . . . . . . . . . . . 63
3.5.2 Proof of the Isomorphism . . . . . . . . . . . . . . . . . . . . . . 67
4 Methods for Obtaining Homomorphic Images 74
5 Transitive Group 80
5.1 Transitive group on 8 letters . . . . . . . . . . . . . . . . . . . . . . . . . 80
5.1.1 Proof of The Isomorphism for The Shape of N . . . . . . . . . . 83
5.1.2 2
•
P GL
2
(11) as a homomorphic Image of 2
∗
8
: ((Z
4
× Z
2
) • D
4
) . 87
vi
5.1.3 (A
5
× A
5
) : 4 as a homomorphic Image of 2
∗
8
: ((Z
4
× Z
2
) • D
4
) . 89
5.1.4 S
5
as a Homomorphic Image of G over N . . . . . . . . . . . . . 100
5.2 The Progenitor 2
∗
14
: (L
2
(7) × 2) . . . . . . . . . . . . . . . . . . . . . . 101
5.3 The Progenitor 2
∗
16
: (2
4
: A
5
) . . . . . . . . . . . . . . . . . . . . . . . 102
5.4 The Progenitor 2
∗
4
: (2
2
: 3) . . . . . . . . . . . . . . . . . . . . . . . . . 103
5.5 The Progenitor 2
∗
6
: (3
2
: 2
2
) . . . . . . . . . . . . . . . . . . . . . . . . 104
5.6 The Progenitor 2
∗
10
: [(2 × 5) : 4] . . . . . . . . . . . . . . . . . . . . . . 104
6 Wreath Product of Permutation Group 106
6.1 Preliminaries . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 106
6.2 The Progenitor 2
∗
6
: Z
3
o Z
2
. . . . . . . . . . . . . . . . . . . . . . . . . 108
6.3 The Progenitor 2
∗
6
: Z
2
o S
3
. . . . . . . . . . . . . . . . . . . . . . . . . 112
7 Monomial Progenitor of P
∗
n
:
m
N 113
7.1 Preliminaries . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 113
7.2 Monomial Progenitor 3
∗
12
:
m
(2
•
A
5
) . . . . . . . . . . . . . . . . . . . . 118
7.3 Monomial Progenitor 3
∗
7
:
m
L
2
(7) . . . . . . . . . . . . . . . . . . . . . 125
7.3.1 A
7
as a Homomorphic Image of 3
∗
7
:
m
L
2
(7) . . . . . . . . . . . 130
7.3.2 3
7
: L
2
(7) as a Homomorphic Image of 3
∗
7
:
m
L
2
(7) . . . . . . . . 133
7.4 Monomial Progenitor 3
∗
21
:
m
A
7
. . . . . . . . . . . . . . . . . . . . . . 140
8 Covering Group 142
9 More Progenitors 146
9.1 2
•
A
5
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 146
9.1.1 The involutory Progenitor 2
∗
24
: (2
•
A
5
) . . . . . . . . . . . . . . 146
9.1.2 The Progenitor 3
∗
24
: (2
•
A
5
) . . . . . . . . . . . . . . . . . . . . 148
9.2 2
•
A
6
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 149
9.2.1 The involutory Progenitor 2
∗
80
: (2
•
A
6
) . . . . . . . . . . . . . . 149
9.2.2 Monomial Progenitor 17
∗
10
:
m
(2
•
A
6
) . . . . . . . . . . . . . . . 151
9.3 3
•
A
6
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 156
9.3.1 The involutory Progenitor 2
∗
18
: (3
•
A
6
) . . . . . . . . . . . . . . 156
9.3.2 Monomial Progenitor 7
∗
6
:
m
(3
•
A
6
) . . . . . . . . . . . . . . . . . 157
9.4 6
•
A
6
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 161
9.4.1 The involutory Progenitor 2
∗
432
: (6
•
A
6
) . . . . . . . . . . . . . 161
9.4.2 Monomial Progenitor 61
∗
36
:
m
(6
•
A
6
) . . . . . . . . . . . . . . . 162
Appendix A: MAGMA Code for DCE of S
5
over A
4
166
Appendix B: MAGMA Code for Isomorphism Type of S
5
170
Appendix C: MAGMA Code for DCE of L
2
(11) × 3 over A
4
172
Appendix D: MAGMA Code for Isomorphism Type of L
2
(11) × 3 198
vii
Appendix E: MAGMA Code for Factoring L
2
(11) × 3 by the Center of G199
Appendix F: MAGMA Code for Isomorphism Type of P GL
2
(11) 201
Appendix G: MAGMA Code for Progenitor 2
∗8
: ((Z
4
× Z
2
) • D
4
) 203
Appendix H: MAGMA Code for Isomorphism Type of ((Z
4
× Z
2
) • D
4
) 206
Appendix I: MAGMA Code for Isomorphism Type of 2
•
P GL
2
(11) 209
Appendix J: MAGMA Code for Isomorphism Type of (A
5
× A
5
) : 4 211
Appendix K: MAGMA Code for The Progenitor 2
∗6
: (Z
3
o Z
2
) 214
Appendix L: MAGMA Code for Monomial Progenitor 3
∗12
:
m
(2
•
A
5
) 216
Appendix M: MAGMA Code for Monomial Progenitor 3
∗7
:
m
L
2
(7) 221
Appendix N: MAGMA Code for DCE of A
7
over L
2
(7) 225
Appendix O: MAGMA Code for Isomorphism Type of 3
7
: L
2
(7) 231
Appendix P: MAGMA Code for Universal Cover of A
6
233
Bibliography 236
viii
List of Tables
1.1 Single Coset Action of 2
3
: S
3
Over S
3
. . . . . . . . . . . . . . . . . . . 12
1.2 Character Table of G = S
5
. . . . . . . . . . . . . . . . . . . . . . . . . . 16
1.3 Character Table of H = S
4
. . . . . . . . . . . . . . . . . . . . . . . . . 16
1.4 Labeling . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
1.5 Permutaion of x = A(x) . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
1.6 Permutaion of y = A(y) . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
3.1 Single Coset Action of S
5
Over A
4
. . . . . . . . . . . . . . . . . . . . . 49
3.2 Z
11
Squares . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68
3.3 Permutation of α : x 7−→ x + 1 . . . . . . . . . . . . . . . . . . . . . . . 68
3.4 Permutation of β : x 7−→ 9x . . . . . . . . . . . . . . . . . . . . . . . . . 68
3.5 Permutation of γ : x 7−→ −1/x = −x
−1
. . . . . . . . . . . . . . . . . . . 69
3.6 Permutation of δ : x 7−→ −x . . . . . . . . . . . . . . . . . . . . . . . . . 69
3.7 Some finite images of the Progenitor 2
∗
5
: D
10
. . . . . . . . . . . . . . . 73
4.1 Conjugacy Classes of S
3
. . . . . . . . . . . . . . . . . . . . . . . . . . . 75
4.2 Some finite images of the Progenitor 2
∗
3
: S
3
. . . . . . . . . . . . . . . 75
5.1 Some finite images of the progenitors 2
∗
8
: N . . . . . . . . . . . . . . . 83
5.2 Conjugacy Classes of L
2
(7) × 2 . . . . . . . . . . . . . . . . . . . . . . . 101
5.3 Some finite images of the Progenitor 2
∗
14
: [L
2
(7) × 2] . . . . . . . . . . 101
5.4 Conjugacy Classes of 2
4
: A
5
. . . . . . . . . . . . . . . . . . . . . . . . . 102
5.5 Some finite images of the Progenitor 2
∗
16
: (2
4
: A
5
)] . . . . . . . . . . . 103
5.6 Some finite images of the Progenitor 2
∗
4
: (2
2
: 3) . . . . . . . . . . . . . 103
5.7 Some finite images of the progenitor 2
∗
6
: (3
2
: 2
2
) . . . . . . . . . . . . 104
5.8 Some finite images of the Progenitor 2
∗
10
: [(2 × 5) : 4] . . . . . . . . . . 105
6.1 γ(4) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 108
6.2 γ(5) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109
6.3 k
∗
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109
6.4 Some finite images of the Progenitor 2
∗
6
: C
3
o C
2
. . . . . . . . . . . . . 110
6.5 Some finite images of the Progenitor 2
∗
6
: C
3
o C
2
. . . . . . . . . . . . . 111
6.6 Some finite images of the Progenitor 2
∗
6
: C
2
o S
3
. . . . . . . . . . . . . 112
ix
7.1 Character Table of G = S
3
. . . . . . . . . . . . . . . . . . . . . . . . . . 115
7.2 Character Table of H = A
3
. . . . . . . . . . . . . . . . . . . . . . . . . 115
7.3 Character Table of G = 2
•
A
5
. . . . . . . . . . . . . . . . . . . . . . . . 119
7.4 Character Table of N = D
10
. . . . . . . . . . . . . . . . . . . . . . . . . 119
7.5 Labeling for t
i
’s . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 121
7.6 Permutaion of x = A(a) . . . . . . . . . . . . . . . . . . . . . . . . . . . 121
7.7 Permutaion of y = A(b) . . . . . . . . . . . . . . . . . . . . . . . . . . . 122
7.8 The Permutation for A = φ(x) . . . . . . . . . . . . . . . . . . . . . . . 128
7.9 The Permutation for B = φ(y) . . . . . . . . . . . . . . . . . . . . . . . 128
7.10 Some Finite Images for 3
∗
7
:
m
L
2
(7) . . . . . . . . . . . . . . . . . . . . 130
9.1 Conjugacy Classes of N = 2
•
A
5
. . . . . . . . . . . . . . . . . . . . . . . 147
9.2 Some finite images of the progenitor 2
∗
24
: (2
•
A
5
) . . . . . . . . . . . . . 148
9.3 Some finite images of the progenitor 3
∗
24
: 2
•
A
5
. . . . . . . . . . . . . . 149
9.4 Conjugacy Classes of N = 2
•
A
6
. . . . . . . . . . . . . . . . . . . . . . . 150
9.5 Character Table of G = 2
•
A
6
. . . . . . . . . . . . . . . . . . . . . . . . 151
9.6 Character Table of H = 3
2
•
8 . . . . . . . . . . . . . . . . . . . . . . . . 151
9.7 Labeling for t
i
’s . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 153
9.8 Permutaion of x = A(x) . . . . . . . . . . . . . . . . . . . . . . . . . . . 154
9.9 Permutaion of y = A(y) . . . . . . . . . . . . . . . . . . . . . . . . . . . 155
9.10 Conjugacy Classes of N = 3
•
A
6
. . . . . . . . . . . . . . . . . . . . . . . 157
9.11 Character Table of G = 3
•
A
6
. . . . . . . . . . . . . . . . . . . . . . . . 158
9.12 Labeling for t
i
’s . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 159
9.13 Permutaion of x = A(x) . . . . . . . . . . . . . . . . . . . . . . . . . . . 159
9.14 Permutaion of y = A(y) . . . . . . . . . . . . . . . . . . . . . . . . . . . 160
9.15 Conjugacy Classes of N = 6
•
A
6
. . . . . . . . . . . . . . . . . . . . . . . 161
9.16 Some finite images of the progenitor 2
∗
432
: (6
•
A
6
) . . . . . . . . . . . . 162
9.17 Nonzero Entries of A(x) and A(y) . . . . . . . . . . . . . . . . . . . . . 165

x
List of Figures
1.1 The Normal Lattice of G
∼
=
2 × U
3
(5) . . . . . . . . . . . . . . . . . . . . 3
1.2 The Normal Lattice of G
∼
=
(A
7
× 3) : 2 . . . . . . . . . . . . . . . . . . 4
1.3 The Normal Lattice of 2
•
2
2
. . . . . . . . . . . . . . . . . . . . . . . . . 6
1.4 The Normal Lattice of 4 • (2 × A
5
) . . . . . . . . . . . . . . . . . . . . . 8
1.5 The Normal Lattice of 2 × A
5
. . . . . . . . . . . . . . . . . . . . . . . . 9
1.6 The Cayley Digram of
2
∗
3
:S
3
tt
x
=t
x
t
. . . . . . . . . . . . . . . . . . . . . . . . 13
1.7 The Normal Lattice of G
∼
=
2
3
: S
3
. . . . . . . . . . . . . . . . . . . . . 14
1.8 The Cayley Diagram of
3
∗
5
:
m
S
5
[xt]
5
. . . . . . . . . . . . . . . . . . . . . . . 24
1.9 The Normal Lattice of G
∼
=
3
4
: S
5
. . . . . . . . . . . . . . . . . . . . . 26
3.1 Cayley Diagram for S
5
Over A
4
. . . . . . . . . . . . . . . . . . . . . . . 48
3.2 Cayley Diagram for L
2
(11) × 3 Over A
4
. . . . . . . . . . . . . . . . . . 57
3.3 Cayley Diagram for L
2
(11) Over A
4
. . . . . . . . . . . . . . . . . . . . 62
3.4 Cayley Diagram for P GL
2
(11) Over D
10
. . . . . . . . . . . . . . . . . . 67
5.1 Cayley Diagram for (A
5
× A
5
) : 4 Over (Z
4
× Z
2
) • D
4
. . . . . . . . . . 98
5.2 The Normal Lattice of (A
5
× A
5
) : 4 . . . . . . . . . . . . . . . . . . . . 99
7.1 Cayley Diagram for A
7
Over L
2
(7) . . . . . . . . . . . . . . . . . . . . . 132
7.2 Cayley Diagram for 3
7
: L
2
(7) Over L
2
(7) . . . . . . . . . . . . . . . . . 138
1
Chapter 1
Introduction
Group theory is a fundamental tool in scientific areas. In mathematics, it is
the studies of groups. The study of permutation groups, which is the basic class of
groups, leads to abstract groups that can be described in a presentation by the group
generators and some suitable relations. Thus, every group G is isomorphic to factore
group of a free product (G
∼
=
F/R
F
), where F is a free group with basis X, and R
F
is a normal subgroup of F generated by ∆ which is a family of words in X, so every
group G has a presentation hF|R
F
i. Moreover, the classification of finite simple group
theorem stated that every finite simple group may be one of the given groups list below.
• Cyclic group Z
p
, where p is prime.
• Alternating group A
n
, where n ≥ 5.
• Lie type group such as L
n
(F ),U (F ),. . .,etc
• The 26 Sporadic groups.
By considring these groups, we have to know that the solution for the extension problem
is not unique for instance, S
3
and Z
3
have the same composition series which is the
products of two cyclic groups of order 2 and 3 but S
3
Z
3
.
As this area is enormous, we are interested in finite groups. Since every fi-
nite group is composed of simple groups and we are able to solve extension problems,
we are interested in finite non-abelian simple groups. Now, it has been shown that
2
progenitors factored by appropriate relations give finite non-abelian simple groups in-
cluding sporadic simple groups. So, we are interested in finding homomorphic images
of progenitors. Moreover, it has been demonstrated, the groups found in this way are
constructed in a manner that reveals some of the important properties of these groups.
We also interested in writing progenitors, permutation and monomial. We have already
written permutation progenitors. In writing monomial progenitors we will obtain new
monomial representations of groups.
The objective of this project is to factor the progenitor m
∗
n
:N by suitable
relations of the form πω(t
1
, . . . , t
n
), where π ∈ N and ω is a word in the symmetric
generators, in order to find finite homomorphic images of the infinte progenitor m
∗
n
:N.
One a finite homomorphic image is found, we determine its isomorphism type in two
ways:
1. We use the composition factors of the image to construct a computer based proof to
determine the type. The solution to the extension problem gives each composition
factor as one of the following types of extensions: direct product, semi-direct
product, central extensions, and mixed extensions.
To ward this, we give a small example that explain each of the four extensions
type.
Example 1.1 (Direct Product Extension:). Consider the following group G
< x, y, t|x
4
, y
3
, (xy)
5
, (x
2
, y), t
2
, (t, xy), (xt)
8
, (yt)
4
, (xyt
x
)
8
> .
Using MAGMA, we obtain the following composition factors.
G
| 2A(2, 5) = U(3, 5)
*
| Cyclic(2)
1
Therefore, G has the following composition series G = G
1
⊇ 1, where G =
(G/G
1
)(G
1
/1) = U
3
(5)C
2
. The normal lattice of G is

3
Figure 1.1: The Normal Lattice of G
∼
=
2 × U
3
(5)
First, we investigate the center of G and we find it is of order 2. Moreover, by
looking at the normal lattice, we find it consists a normal subgroup of order 2.
Thus, we might have a direct product of [2] by the Unitary group [3] = U
3
(5).
> D:=DirectProduct(CyclicGroup(2),NL[3]);
> s:=IsIsomorphic(D,G1);s;
true
The MAGMA loop, confirms that we have a direct product of a cyclic group of
order 2 by U
3
(5). By using ATLAS, we were able to write a presentation for the
Unitary group.
< a, b|a
3
, b
5
, (ab)
7
, (ab
−1
)
7
, aba
−1
b
2
aba
−1
bab
2
a
−1
b >
Since G is a direct product extension, element of [2] commutes with the elements
of [3]=U
3
(5). Thus, a presentation for G becomes
> H<a,b,c>:=Group<a,b,c|aˆ3,bˆ5,(a
*
b)ˆ7,(a
*
bˆ-1)ˆ7,
> a
*
b
*
aˆ-1
*
bˆ2
*
a
*
b
*
aˆ-1
*
b
*
a
*
bˆ2
*
aˆ-1
*
b,cˆ2,(c,a),(c,b)>;#H;
252000
> f1,H1,k1:=CosetAction(H,sub<H|Id(H)>);
> s:=IsIsomorphic(H1,G1);s;
true
Henc, G
∼
=
2 × U
3
(5).
Example 1.2 (Semi-direct Extension:). Consider the following group
< x, y, z, t|x
3
, y
3
, z
2
, (x, y), x
z
= y, y
z
= x, t
2
, (t, x), (yt)
3
, (yztt
y
)
10
, (xyt
z
t)
5
>,

4
where
x ≈ (456), y ≈ (123), and z ≈ (15)(26)(34)
G has the following composition factors.
G
| Cyclic(2)
*
| Alternating(7)
*
| Cyclic(3)
1
Therefore, the composition series for this group is
G
1
⊇ G
2
⊇ 1,
where G = (G
1
/G
2
)(G
2
/1) = C
2
A
7
C
3
. The normal lattice of G is
Figure 1.2: The Normal Lattice of G
∼
=
(A
7
× 3) : 2
The center of G is of order 1 which indicates that we do not have a central
extension. Moreover, by using MAGMA, we find that the two minimal normal
subgroups of G is one of order 3 and the other is of order 2520. So, we can say
that we have C
3
× A
7
with order 7560. By looking at the normal lattice of G, we
5
find that [4] is the isomorphic image of order 7560. We obtain that [4]
∼
=
C
3
× A
7
.
By using ATLAS, we were able to write the symmetric presentation for G
1
.
< a, b, c|a
3
, b
5
, (ab)
7
, (aa
b
)
2
, (ab
−2
ab
2
)
2
, c
3
, (a, c), (b, c) > .
Since we have G
1
= 3 × A
7
, G/G
1
∼
=
C
2
. By viewing the normal lattice, we find
that it does not have a normal subgroup of order 2. Thus, we have a semi-direct
product of G
1
= 3 × A
7
by C
2
. Next, we are looking for an element d of order 2
in G but outside [4].
for g in G1 do if Order(g) eq 2 and g notin NL[4]
and G1 eq sub<G1|NL[4],g>
then U:=g; break; end if; end for;
Since we have a semi-direct extension, we want to find the action of d on the
generators of G
1
a, b, and c. In order to do this, we use the Schreier System for
G
1
.
a
d
= ab
−1
a
−1
b
2
ab
−1
a
−1
.
b
d
= ab
2
aba
−1
b
2
.
c
d
= c
−1
.
Finally, we were able to write a presentation for G as below.
< a, b, c, d|a
3
, b
5
, (ab)
7
, (aa
b
)
2
, (ab
−2
ab
2
)
2
, c
3
, (a, c), (b, c),
d
2
, a
d
= ab
−1
a
−1
b
2
ab
−1
a
−1
, b
d
= ab
2
aba
−1
b
2
, c
d
= c
−1
>
Hence, we have solved the extension type of G.
G
∼
=
(3 × A
7
) : 2
Example 1.3 (Central Extension:). Consider the group
G = D
4
=< a, b|a
4
, b
2
, (ab)
2
>
The composition factors of G are as below.

6
G
| Cyclic(2)
*
| Cyclic(2)
*
| Cyclic(2)
1
Therefore, the composition series is
G
1
⊇ G
2
⊇ 1,
where G = (G
1
/G
2
)(G
2
/1) = C
2
C
2
C
2
. The normal lattice of G is
Figure 1.3: The Normal Lattice of 2
•
2
2
Since the center of G is of order 2, indicates that we might have a central extension.
By viewing the normal lattice of G, we see that [2] is of order 2. Therefore, it is
possible that [2] is the center of G.
> Center(G1);
Permutation group acting on a set of cardinality 8
Order = 2
(1, 5)(2, 4)(3, 8)(6, 7)
> Center(G1) eq NL[2];
true
The above loop confirms that [2] is the center of G. Thus, we have a central
extension of [2] by C
2
C
2
. Now, we want to factor G by [2] to determine the
isomorphism type of q
∼
=
G/[2].
7
> q,ff:=quo<G1|NL[2]>;
> IsAbelian(q);
true
> X:=AbelianGroup(GrpPerm,[2,2]);
> s:=IsIsomorphic(X,q);
> s;
true
We find out that q
∼
=
2
2
. A presentation for q is
H =< a, b|a
2
, b
2
, (a, b) > .
> f1,H1,k1:=CosetAction(H,sub<H|Id(H)>);
> s:=IsIsomorphic(H1,q);
> s;
true
Now, we want to write a presentation for G by writing the generators of q in terms
of the center x.
> T:=Transversal(G1,NL[2]);
> ff(T[2]) eq q.1;
true
> ff(T[3]) eq q.2;
true
> a:=T[2];
> b:=T[3];
> x:=NL[2].1;
for i in [1..2] do if aˆ2 eq xˆi then i; end if; end for;
for i in [1..2] do if bˆ2 eq xˆi then i; end if; end for;
for i in [1..2] do if (a,b) eq xˆi then i; end if; end for;
Now, we want to write a presentation for G given by H by inserting x as a
generator of [2] and writing the generators of q in trems of the center x.
HH =< x, a, b|x
2
, a
2
= x, b
2
, (a, b) = x >
> f2,H2,k2:=CosetAction(HH,sub<HH|Id(HH)>);
> s:=IsIsomorphic(H2,G1);
> s;
true

8
Hence, G
∼
=
2
•
2
2
.
Example 1.4 (Mixed Extension:). Consider the group
G =< x, y, t|x
5
, y
2
, (xy)
2
, t
2
, (t, y), (xyt
x
2
)
2
, (xtt
x
)
3
, (ytt
x
2
t
x
)
2
>,
where x ≈ (12345) and y ≈ (14)(23). By using MAGMA, we get the following
composition factors of G.
G
| Alternating(5)
*
| Cyclic(2)
*
| Cyclic(2)
*
| Cyclic(2)
1
Therefore, the composition series is
G
1
⊇ G
2
⊇ G
3
⊇ 1,
where G = (G
1
/G
2
)(G
2
/G
3
)(G
3
/1) = A
5
C
2
C
2
C
2
. The normal lattice of G is
Figure 1.4: The Normal Lattice of 4 • (2 × A
5
)

9
Since the center of G is of order 2, we might be have a central extension. Now,
we want to find the maximal abelian group in G by running the following loop
> for i in [1..11] do if IsAbelian(NL[i]) then i;
end if; end for;
1
2
3
4
5
Thus, the maximal abelian group is [5] which is of order 4.
> X:=AbelianGroup(GrpPerm,[4]);
> s:=IsIsomorphic(X,NL[5]);s;
true
We confirm that G
2
= C
4
is the isomorphism type of [5]. Moreover, [5] is not the
center of G. Thus, we have a mixed extension of [5] by q where q is the isomorphic
image of G/G
2
= G/[5]. By looking at the normal lattice of q below, we see that
Figure 1.5: The Normal Lattice of 2 × A
5
it has C
2
and A
5
as normal subgroups. So, we have a direct product of C
2
by A
5
.
> q,ff:=quo<G1|NL[5]>;
> D:=DirectProduct(nl[2],Alt(5));
> s:=IsIsomorphic(D,q);s;
true
A presentation for q found by
10
H:=sub<q|q.1,q.2,q.3>;
FPGroup(H);
H<a,b,c>:=Group<a,b,c|aˆ5,bˆ2,cˆ2,(aˆ-1
*
b)ˆ2,(b
*
c)ˆ2,
(c
*
aˆ-1)ˆ3>;
> f1,H1,k1:=CosetAction(H,sub<H|Id(H)>);
> s:=IsIsomorphic(H1,q);s;
true
Now, we want to write the generators of q in terms of the generator of [5] and find
its action on the generators of [5].
> T:=Transversal(G1,NL[5]);
> a:=T[2];
> b:=T[3];
> c:=T[4];
> x:=NL[5].1;
for i in [1..4] do if xˆa eq xˆi then i; end if; end for;
for i in [1..4] do if xˆb eq xˆi then i; end if; end for;
for i in [1..4] do if xˆc eq xˆi then i; end if; end for;
for i in [1..4] do if (c
*
aˆ-1)ˆ3 eq xˆi then i;
end if; end for;
We now want to write a presentation for G given by H, by inserting x as a
generator of [5].
H =< x, a, b, c|x
4
, a
5
, b
2
, c
2
, (a
−1
b)
2
, (bc)
2
, (ca
−1
)
3
= x
3
, x
a
= x, x
b
= x
3
, x
c
= x > .
Finally, we check if it is isomorphic to G
1
.
> f1,H1,k1:=CosetAction(H,sub<H|Id(H)>);
> s:=IsIsomorphic(H1,G1);s;
true
Hence, we have proved that G
∼
=
4 • (2 × A
5
).
2. We perform a double coset enumeration of the image over N and obtain a Cayley
graph of the image over N . We use this graph to prove by hand that the image is
indeed isomorphic to the group given in 1.
To ward the end of this, we give small examples to explain the process of the double
coset enumeration when the progenitor is involutory then when the progenitor is
monomial.

11
Example 1.5. Consider the group G
∼
=
hx, y, t|x
3
, y
2
, (xy)
2
, t
2
, (t, xy), (t, y
x
)i fac-
tored by tt
x
= t
x
t, where G = 2
∗
3
: S
3
, N = S
3
= hx, yi = h(123), (12)i and
t = t
1
. The main goal of this example is to show that G =
2
∗
3
:S
3
t
1
t
2
=t
2
t
1
∼
=
2
3
: S
3
. If
we conjugate the previous relation by all elements in S
3
, we obtain:
12 ≈ 21, 32 ≈ 23, and 13 ≈ 31.
First, we start with the double coset NeN denoted by [∗] which consists of the
single coset N. Therefore, the number of right cosets in N is equal to
|N|
|N|
=
6
6
= 1.
Then, we consider the double coset NwN , where w is a word of length one. Since
N is transitive on T = {1, 2, 3}, The orbit of N on T is {1,2,3}. Thus, we pick a
representive t
1
and determine its double coset.
Consider Nt
1
N = {Nt
1
, Nt
2
, Nt
3
}. We denote the double coset Nt
1
N by [1].
Now, we determine the orbits of N
1
= {n ∈ N|t
n
1
= t
1
} = {e, (23)} = N
(1)
on
T = {1, 2, 3} and these are {1} and {2, 3}, and consider the double cosets Nt
1
t
i
N
for one t
i
from each orbit of N
1
say t
1
and t
2
, respectivelly, and determine the
double cosets that contain Nt
1
t
1
and Nt
1
t
2
. We see that Nt
1
t
1
∈ [∗], so one
symmetric generator will go back to [∗], and N t
1
t
2
∈ [12] is a new double coset.
Now, N
12
= hei, but N(t
1
t
2
)
(12)
= Nt
2
t
1
relation
= Nt
1
t
2
⇒ (12) ∈ N
(12)
. So,
N
(12)
≥ h(12)i. The number of right cosets in [12] is equal to
|N|
|N
(12)
|
=
6
2
= 3. The
orbits of N
(12)
on {1,2,3} are {1,2} and {3}. Pick a representative from each orbit,
say t
2
and t
3
respectivelly, to determine the double cosets that contain Nt
1
t
2
t
2
and Nt
1
t
2
t
3
. It is obvious to see that Nt
1
t
2
t
2
= Nt
1
∈ [1], and Nt
1
t
2
t
3
∈ [123] is
a new double coset.
Now, N
123
= hei, but N (t
1
t
2
t
3
)
(12)
= N t
2
t
1
t
3
relation
= Nt
1
t
2
t
3
⇒ (12) ∈ N
(123)
.
Similarly, (123) ∈ N
(123)
. So, N
(123)
≥ h(12), (123)i
∼
=
S
3
. The number of right
cosets in [123] is equal to
|N|
|N
(123)
|
=
6
6
= 1. The orbits of N
(123)
on {1,2,3} is
{1,2,3}. By picking t
3
from the orbit, we see that Nt
1
t
2
t
3
t
3
= Nt
1
t
2
∈ [12]. Thus,
three symmetric generators will go back to [12].
The set of right cosets is closed under right multiplication by t
0
i
s where i = 1, 2, 3

12
. Thus, we can determine the index of N in G. We conclude that
|G| ≤ (|N| +
|N|
|N
(1)
|
+
|N|
|N
(12)
|
+
|N|
|N
(123)
|
) × |N|
|G| ≤ (1 + 3 + 3 + 1) × 6
|G| ≤ (8 × 6) = 48.
Table 1.1: Single Coset Action of 2
3
: S
3
Over S
3
Label Single Cosets x ≈ (123) y ≈ (12) t
1
1 N 1 N 1 N 2 N t
1
2 Nt
1
3 N t
2
3 N t
2
1 N t
1
t
1
= N
3 Nt
2
4 N t
3
2 N t
1
5 N t
2
t
1
4 Nt
3
2 N t
1
4 N t
3
6 N t
3
t
1
5 Nt
1
t
2
7 N t
2
t
3
5 N t
2
t
1
3 N t
1
t
2
t
1
= Nt
2
6 Nt
1
t
3
5 N t
2
t
1
7 N t
2
t
3
4 N t
1
t
3
t
3
= Nt
1
7 Nt
2
t
3
6 N t
3
t
1
6 N t
1
t
3
8 N t
2
t
3
t
1
= Nt
1
t
2
t
3
8 Nt
1
t
2
t
3
8 N t
2
t
3
t
1
8 N t
2
t
1
t
3
7 N t
1
t
2
t
3
t
1
= Nt
2
t
3
Next, we note that G = 2
∗
3
: S
3
=< t
1
, x, y > acts on the eight cosets above
and the actions of t, x, y on the eight cosets is well-defined. Thus, we have a
homomorphism f : G −→ S
8
. Then f(G) =< f (x), f(y), f(t) >; that is, the
homomorphic image of 2
∗
3
: S
3
is of the order | < f(x), f (y), f(t) > | = 48. Since
t has exactly 3 conjugates, we have f(G)
∼
=
< f(x), f(y), f(t) >, where
f(x) = (234)(576).
f(y) = (23)(67).
f(t) = (12)(35)(46)(78). (see table 1)
Hence,
⇒ G/Kerf
∼
=
< f(x), f(y), f(t) >= f(G)
⇒ |G/Kerf|
∼
=
|f(G)|
⇒ |G| = |Kerf| × |f(G)|
⇒ |G| ≥ |Kerf| × 48.

13
But from above we observed that |G| ≤ 48. This can also be seen from the Cayley
diagram below.
Hence,
|G| = 48 ⇒ |Kerf| = 1
⇒ G
∼
=
< f(x), f(y), f(t) >
Please see the Cayley diagram of G =
2
∗
3
:S
3
tt
x
=t
x
t
over S
3
below.
Figure 1.6: The Cayley Digram of
2
∗
3
:S
3
tt
x
=t
x
t
G =< f(x), f(y), f(t) >.
Now, we want to show that 2
3
: S
3
is the homomorphic image of
2
∗
3
:S
3
tt
x
=t
x
t
.
G = hx, y, t|x
3
, y
2
, (xy)
2
, t
2
, (t, xy), (t, y
x
), tt
x
= t
x
ti
By using MAGMA, we have the composition series
G ⊇ G
1
⊇ G
2
⊇ G
3
⊇ G
4
⊇ 1,
where
G = (G/G
1
)(G
1
/G
2
)(G
2
/G
3
)(G
3
/G
4
)(G
4
/1) = (G/G
1
)(G
1
/1) = C
2
C
2
C
2
C
3
C
2
.
The normal lattice of G is

14
Figure 1.7: The Normal Lattice of G
∼
=
2
3
: S
3
We want to determine the isomorphism type of this group. We find that the center
of G is of order 2. So, we might have a central extension. Now, we want to see if
[4] is an abelian group or not.
> X:=AbelianGroup(GrpPerm,[2,2,2]);
> s:=IsIsomorphic(X,NL[4]);s;
true
We confirm that G2 = 2 × 2 × 2 is the isomorphism type of [4]. Since [4] is an
abelian group of G, G is not a central extension. Now, we want to factor G by [4]
to find H such that G/[4]
∼
=
H.
> q,ff:=quo<G1|NL[4]>;
> s:=IsIsomorphic(q,Sym(3));s;
true
We show that H
∼
=
S
3
and a presentation for H is < A, B|A
3
, B
2
, (AB)
2
>. Next,
we want to find the right cosets of G/[4] to store and write the two generators of
H in terms of the generators of [4].
T:=Transversal(G1,NL[4]);
a:=T[2]; b:=T[3];
x:=NL[4].1; y:=NL[4].2; z:=NL[4].3;

15
The following loops will determine the action of a and b on x, y, and z.
for i,j,l in [1..2] do if xˆa eq xˆi
*
yˆj
*
zˆl then i,j,l;
end if; end for;
for i,j,l in [1..2] do if xˆb eq xˆi
*
yˆj
*
zˆl then i,j,l;
end if; end for;
Using MAGMA, we highlight the relation between them and write a presentation
for G. At the end, we check if this presentation is isomorphic with 2
3
: S
3
,
> M<x,y,z,a,b>:=Group<x,y,z,a,b|xˆ2,yˆ2,zˆ2,(x,y),
(x,z),(y,z),aˆ3,bˆ2,(a
*
b)ˆ2,xˆa=x
*
z,xˆb=x
*
z,yˆa=z,
yˆb=y
*
z,zˆa=y
*
z,zˆb=z>;
> #M;
48
> f1,M1,k1:=CosetAction(M,sub<M|Id(M)>);
> s:=IsIsomorphic(M1,G1);s;
true
Since the above presentaion have been written with the action of the generators
of H on the generators of [4], G is a semi-direct product. So, we obtain that
G
∼
=
2
3
: S
3
.
Example 1.6. Consider the group N = S
5
. A presentation of S
5
is
hx, y|x
5
, y
2
, (xy)
4
, (x, y)
3
i,
where x ≈ (12345) and y ≈ (12). We want to write a presentation for the
monomial progenitor 3
∗
5
:
m
S
5
. Thus, we have to induce a linear character of
a subgroup H of G. By looking at the character table ofS
5
, we find that the
largest index is 5. Thus, we will induce from a subgroup of index 5 such that
|H| =
120
[S
5
:H]
=
120
5
= 24 = |S
4
|. We will induce a linear character of a subgroup
S
4
, say χ
2
, up to G = S
5
.
Moreover, we have to find a representation B of H such that B(χ
2
(g)) is equal to
the value of χ
2
of H at g ∈ H. So,
B(1) = 1, B((25)(34)) = 1, B((34)) = −1, B((235)) = 1, and B((2453)) = −1.

16
Table 1.2: Character Table of G = S
5
χ C
1
C
2
C
3
C
4
C
5
C
6
C
7
χ
1
1 1 1 1 1 1 1
χ
2
1 -1 1 1 -1 1 -1
χ
3
4 -2 0 1 0 -1 1
χ
4
4 2 0 1 0 -1 -1
χ
5
5 1 1 -1 -1 0 1
χ
6
5 -1 1 -1 1 0 -1
χ
7
6 0 -2 0 0 1 0
Table 1.3: Character Table of H = S
4
Classes 1 (25)(34) (34) (235) (2453)
Size 1 3 6 8 6
Order 1 2 2 3 4
χ
χ
1
1 1 1 1 1
χ
2
1 1 -1 1 -1
A monomial representation of G is given by
A(x) =
B(t
1
xt
−1
1
) B(t
1
xt
−1
2
) B(t
1
xt
−1
3
) B(t
1
xt
−1
4
) B(t
1
xt
−1
5
)
B(t
2
xt
−1
1
) B(t
2
xt
−1
2
) B(t
2
xt
−1
3
) B(t
2
xt
−1
4
) B(t
2
xt
−1
5
)
B(t
3
xt
−1
1
) B(t
3
xt
−1
2
) B(t
3
xt
−1
3
) B(t
3
xt
−1
4
) B(t
3
xt
−1
5
)
B(t
4
xt
−1
1
) B(t
4
xt
−1
2
) B(t
4
xt
−1
3
) B(t
4
xt
−1
4
) B(t
4
xt
−1
5
)
B(t
5
xt
−1
1
) B(t
5
xt
−1
2
) B(t
5
xt
−1
3
) B(t
5
xt
−1
4
) B(t
5
xt
−1
5
)
To get the representation of monomial representations A(x) and A(y), which are
represented by 5 × 5 matrices, from B(u), we extend B to give a presentation of
G. Thus,
A(x) =
B(x), if x ∈ H
0, if x /∈ H.
.
Now, we will be able to find the monomial representations A(x) and A(y) which are
represented by 5 × 5 matrices. Moreover,By using MAGMA, we run the following
code to obtain the right cosets of S
5
/H.
17
> T:=RightTransversal(G1,N);
> T;
{
Id(G1),
(1, 2),
(1, 3, 4, 5),
(1, 4)(2, 3, 5),
(1, 5, 3)(2, 4)
}
Thus,
G = H
t
1
1
∪H
t
2
(12) ∪H
t
3
(1345) ∪H
t
4
(14)(235) ∪H
t
5
(153)(24).
We are now in a position to give the monomial representation of the progrnitor
3
∗
5
:
m
S
5
.
A(x) =
B((12345)) B((2345)) B((12)) B((1543)) B((14)(253))
B((1345)) B((13452)) B(1) B((12543)) B((15324))
B((14)(235)) B((14235)) B((13452)) B(1) B((12543))
B((153)(24)) B((15324)) B((14235)) B((13452)) B(1)
B((5432)) B((12543)) B((15324)) B((14235)) B((13452))
Now,
A(x) =
0 −1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1
−1 0 0 0 0
Similarly, we can find the monomial representation for A(y).
A(y) =
0 1 0 0 0
1 0 0 0 0
0 0 −1 0 0
0 0 0 −1 0
0 0 0 0 −1

18
Since the entries of the two monomial matrices are ±1, the entries are in Z
3
.
Hence, t
i
’s are of order 3. Since the number of t
i
’s is equal to [S
5
: S
4
] = 5, We
label them as shown in the table below.
Table 1.4: Labeling
1 2 3 4 5 6 7 8 9 10
t
1
t
2
t
3
t
4
t
5
t
−1
1
t
−1
2
t
−1
3
t
−1
4
t
−1
5
Now, A(x) is a monoial automorphism of < t
1
> ∗ < t
2
> ∗ < t
3
> ∗ < t
4
> ∗ <
t
5
> given by a
ij
= a ⇒ t
i
→ t
a
j
. Thus, a
12
= −1 or t
1
→ t
−1
2
. So, A(x) takes 1
to 7 by our labeling.
Table 1.5: Permutaion of x = A(x)
1 2 3 4 5 6 7 8 9 10
t
1
t
2
t
3
t
4
t
5
t
−1
1
t
−1
2
t
−1
3
t
−1
4
t
−1
5
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
t
−1
2
t
3
t
4
t
5
t
−1
1
t
2
t
−1
3
t
−1
4
t
−1
5
t
1
7 3 4 5 6 2 8 9 10 1
So, A(x) = (1, 7, 8, 9, 10)(2, 3, 4, 5, 6).
Now. A(y) is a monomial automorphism (permutation) of < t
1
> ∗ < t
2
> ∗ <
t
3
> ∗ < t
4
> ∗ < t
5
> given by a
ij
= a ⇒ t
i
→ t
a
j
. Thus, a
12
= 1 or t
1
→ t
2
. So,
A(y) takes 1 to 2 by our labeling.
Table 1.6: Permutaion of y = A(y)
1 2 3 4 5 6 7 8 9 10
t
1
t
2
t
3
t
4
t
5
t
−1
1
t
−1
2
t
−1
3
t
−1
4
t
−1
5
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
t
2
t
1
t
−1
3
t
−1
4
t
−1
5
t
−1
2
t
−1
1
t
3
t
4
t
5
2 1 8 9 10 7 6 3 4 5
Then, A(y) = (1, 2)(3, 8)(4, 9)(5, 10)(6, 7).
So, S
5
= hA(x), A(y)i = h(1, 7, 8, 9, 10)(2, 3, 4, 5, 6), (1, 2)(3, 8)(4, 9)(5, 10)(6, 7)i.
We are now be able to give a monomial presentation of the progenitor 3
∗
5
:
m
S
5
.

19
We fix one the five t
i
’s, say t
1
and call it t. Next, compute the normalizer of the
subgroup < t
1
> in S
5
. We therefore need to compute the set stabilizer in S
5
of
the set {t
1
, t
2
1
= t
−1
1
} = {1, 6}.
> S:=Sym(10);
> xx:=S!(1,7,8,9,10)(2,3,4,5,6);
> yy:=S!(1,2)(3,8)(4,9)(5,10)(6,7);
> N:=sub<S|xx,yy>;
> SS:=Stabiliser(N,{1,6});
> SS;
(2, 3, 4)(7, 8, 9),
(3, 5, 4)(8, 10, 9),
(1, 6)(2, 10, 4, 8)(3, 7, 5, 9)
Thus, the normlizer of < t
1
> generated by
(2, 3, 4)(7, 8, 9) = x
2
yx
−1
y,
(3, 5, 4)(8, 10, 9) = x
−1
yxyx
−1
, and
(1, 6)(2, 10, 4, 8)(3, 7, 5, 9) = yx
−1
.
The monomial progenitor 3
∗
5
:
m
S
5
has
hx, y, t|x
5
, y
2
, (xy)
4
, (x, y)
3
, t
3
, (t, x
2
yx
−1
y), (t, x
−1
yxyx
−1
), t
yx
−1
t
−2
i.
as a (symmetric) presentation. This progenitor is infinite, and in order to make it
finite we add a suporting relator such as (xt)
k
and run the progenitor in MAGMA
to obtain a homomorphic image of 3
∗
5
:
m
S
5
.
> for k in [1..5] do
for> G<x,y,t>:=Group<x,y,t|xˆ5,yˆ2,(x
*
y)ˆ4,(x,y)ˆ3,
tˆ3,(t,xˆ2
*
y
*
xˆ-1
*
y),(t,xˆ-1
*
y
*
x
*
y
*
xˆ-1),
tˆ(y
*
xˆ-1)
*
tˆ-2,(x
*
t)ˆk>;k,#G; end for;
1 2
2 2
3 6
4 2
5 9720
Thus, we have G =
3
∗
5
:
m
S
5
[xt]
5
∼
=
3
4
: S
5
.
Now, we are interesting in constructing the Cayley diagram of 3
∗
5
:
m
S
5
by proc-
ceding the DCE technique.

20
Consider the progenitor G =
3
∗
5
:
m
S
5
[xt]
5
, where S
5
is generated by
hx, yi = h(1, 7, 8, 9, 10)(2, 3, 4, 5, 6), (1, 2)(3, 8)(4, 9)(5, 10)(6, 7)i.
Let t = t
1
. Thus,
[xt]
5
= 1
x
5
t
x
4
t
x
3
t
x
2
t
x
t = 1
t
10
t
9
t
8
t
7
t
1
= 1
t
10
t
9
= t
−1
1
t
−1
7
t
−1
8
t
10
t
9
= t
6
t
2
t
3
.
Therefore, N t
10
t
9
= N t
6
t
2
t
3
. By conjugation with all n ∈ S
5
, we obtain the
following relations.
43 = 10
71 ≈ 7110 ≈ 1107, 34 = 7101 ≈ 1017 ≈ 1710,
26 = 9810 ≈ 1098 ≈ 8109, 62 = 8910 ≈ 1089 ≈ 9108,
23 = 1910 ≈ 9101 ≈ 1019, 32 = 1091 ≈ 1109 ≈ 9110,
42 = 1018 ≈ 8101 ≈ 1810, 24 = 1108 ≈ 1081 ≈ 8110,
46 = 1087 ≈ 7108 ≈ 8710, 64 = 8107 ≈ 1078 ≈ 7810,
63 = 9710 ≈ 1097 ≈ 7109, 36 = 1079 ≈ 9107 ≈ 7910,
109 = 623 ≈ 236 ≈ 362, 910 = 263 ≈ 632 ≈ 326,
101 = 324 ≈ 243 ≈ 432, 110 = 234 ≈ 342 ≈ 423,
107 = 634 ≈ 463 ≈ 346, 710 = 364 ≈ 436 ≈ 643,
108 = 642 ≈ 264 ≈ 426, 810 = 462 ≈ 246 ≈ 624,
54 = 718 ≈ 187 ≈ 871, 45 = 178 ≈ 817 ≈ 781,
98 = 562 ≈ 625 ≈ 256, 89 = 625 ≈ 265 ≈ 526,
71 = 345 ≈ 453 ≈ 534, 17 = 354 ≈ 543 ≈ 435,
25 = 189 ≈ 918 ≈ 891, 52 = 819 ≈ 198 ≈ 981,
65 = 879 ≈ 987 ≈ 798, 56 = 789 ≈ 897 ≈ 978,
87 = 456 ≈ 564 ≈ 645, 78 = 465 ≈ 546 ≈ 654,
18 = 245 ≈ 524 ≈ 452, 81 = 425 ≈ 542 ≈ 254,

21
91 = 523 ≈ 352 ≈ 235, 19 = 253 ≈ 325 ≈ 532,
79 = 356 ≈ 635 ≈ 563, 97 = 536 ≈ 653 ≈ 365,
53 = 791 ≈ 179 ≈ 917, 35 = 197 ≈ 971 ≈ 719.
The main goal of this example is to show that G =
3
∗
5
:
m
S
5
t
10
t
9
=t
6
t
2
t
3
∼
=
3
4
: S
5
. Elements
of 3
∗
5
is of the form < t
1
> ∗ . . . ∗ < t
5
>= {t
1
, t
2
1
= t
−1
1
} ∗ . . . ∗ {t
5
, t
2
5
= t
−1
5
}.
First, we start with the double coset NeN denoted by [∗] which consists of the
single coset N . Then, we consider the double coset NwN, where w is a word of
length one. Since the orbit of N is {1,2,3,4,5,6,7,8,9,10}, pick a representitive, say
t
1
, and determine the double coset that contains N t
1
N.
Consider Nt
1
N = {Nt
1
, . . . , Nt
10
} = Nt
2
N = . . . = Nt
10
N, which is denoted
by [1]. N
1
=< (2, 3, 4)(7, 8, 9), (3, 5, 4)(8, 10, 9) >= N
(1)
. Thus, the number of
right cosets in [1] is equal to
|N|
|N
(1)
|
=
120
12
= 10. The orbits of N
(1)
on T =
{1, 2, 3, 4, 5, 6, 7, 8, 9, 10} are {1}, {6}, {2,3,4,5}, and {7,8,9,10}. By our labeling,
it is obvious to see that
Nt
1
t
1
= Nt
2
1
= Nt
−1
1
= Nt
6
∈ [1], so 1 symmetric generator will stay on [1].
Nt
1
t
6
= N ∈ [∗], so 1 symmetric generator will take back on [∗].
Nt
1
t
2
∈ [12].
Nt
1
t
7
∈ [17].
Consider Nt
1
t
2
N, which is denoted by [12]. N
12
= N
(12)
is generated by
< (3, 5, 4)(8, 10, 9), (1, 2)(3, 8)(4, 9)(5, 10)(6, 7), (1, 2)(3, 10, 4, 8, 5, 9)(6, 7),
(1, 2)(3, 9, 5, 8, 4, 10)(6, 7) > .
Thus, the number of right cosets in [12] is equal to
|N|
|N
(12)
|
=
120
6
= 20. The orbits
of N
(12)
on T = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} are {1,2}, {6,7}, and {3,4,5,8,9,10}. Pick
t
2
, t
7
, and t
3
, respectively, from each orbit and determin the double coset that
contains each one of them. We see that
Nt
1
t
2
t
2
= Nt
1
t
2
2
= Nt
1
t
−1
2
= Nt
1
t
7
∈ [17], so 2 symmetric generators will take to
[17].
Nt
1
t
2
t
7
= Nt
1
t
2
t
−1
2
= Nt
1
∈ [1], so 2 symmetric generator will take back to [1].
Nt
1
t
2
t
3
∈ [123].

22
Consider Nt
1
t
7
N, which is denoted by [17]. N
17
= N
(17)
is generated by
< (3, 5, 4)(8, 10, 9), (1, 7)(2, 6)(3, 4)(8, 9),
(1, 7)(2, 6)(3, 5)(8, 10), (1, 7)(2, 6)(4, 5)(9, 10) >= N
(17)
.
Therefore, the number of right cosets in [17] is equal to
|N|
|N
(17)
|
=
120
6
= 20. The
orbits of N
(17)
are {1,7}, {2,6}, {3,4,5}, and {8,9,10}. The double coset that
contains t
7
, t
2
, t
3
, and t
8
is as the following
Nt
1
t
7
t
7
= Nt
1
t
2
2
t
2
2
= Nt
1
t
2
t
3
2
= Nt
1
t
2
∈ [12], so 2 symmetric generators will take
to [12].
Nt
1
t
7
t
2
= Nt
1
t
−1
2
t
2
= Nt
1
∈ [1], so 2 symmetric generator will take back to [1].
Consider Nt
1
t
7
t
3
N which is denoted by [173].
Because the relation
Nt
1
t
7
t
3
= N(t
1
t
2
t
3
)
(1,8,10,7,9)(2,4,6,3,5)
= Nt
8
t
4
t
5
where Nt
8
t
4
t
5
∈ [123].
There exist {n ∈ N|N(t
1
t
2
t
3
)
n
= Nt
8
t
4
t
5
}.
Thus, N(t
1
t
2
t
3
)
(1,8,10,7,9)(2,4,6,3,5)
= Nt
8
t
4
t
5
.
[173] = [123]
Therefore, N t
1
t
7
t
3
N is not a new double coset and collapses ⇒ three symmetric
genertators will take to [123].
Consider Nt
1
t
7
t
8
N which is denoted by [178].
Because the relation
Nt
1
t
7
t
8
= N(t
1
t
7
)
(1,4,8,6,9,3)(2,10)(5,7)
= Nt
4
t
5
where Nt
4
t
5
∈ [17].
There exist {n ∈ N|N(t
1
t
7
)
n
= Nt
4
t
5
}.
Thus, N(t
1
t
7
)
(1,4,8,6,9,3)(2,10)(5,7)
= Nt
4
t
5
.

23
[178] = [17]
Therefore, N t
1
t
7
t
8
N is not a new double coset and collapses ⇒ three symmetric
genertators will take to [17].
Consider Nt
1
t
2
t
3
N, which is denoted by [123]. N
123
= N
(123)
is generated by
N
(123)
=< (2, 3)(4, 5)(7, 8)(9, 10), (1, 6)(2, 9, 3, 10)(4, 8, 5, 7),
(1, 6)(2, 10, 3, 9)(4, 7, 5, 8) > .
Therefore, the number of right cosets in [123] is equal to
|N|
|N
(123)
|
=
120
4
= 30. The
orbits of N
(123)
are {1,6}, {2,3,9,10}, and {4,5,8,7}. It is obvious to see that
Nt
1
t
2
t
3
t
8
= Nt
1
t
2
t
3
t
−1
3
= Nt
1
t
2
∈ [12], so 4 symmetric generators will take back
to [12].
Consider Nt
1
t
2
t
3
t
3
N which is denoted by [1233].
Because the relation
Nt
1
t
2
t
3
t
3
= N(t
1
t
2
t
3
)
(1,7,9,8,10)(2,4,3,5,6)
= Nt
7
t
4
t
5
,
where Nt
7
t
4
t
5
∈ [123].
There exist {n ∈ N|N(t
1
t
2
t
3
)
n
= Nt
7
t
4
t
5
}.
Thus, N(t
1
t
2
t
3
)
(1,7,9,8,10)(2,4,3,5,6)
= Nt
7
t
4
t
5
.
[1233] = [123]
Therefore, Nt
1
t
2
t
3
t
3
N is not a new double coset and collapses ⇒ three symmetric
genertators will take to [123].
Consider Nt
1
t
2
t
3
t
6
N which is denoted by [1236].
Because the relation
Nt
1
t
2
t
3
t
6
= N(t
1
t
7
)
(1,3,9,5)(2,7)(4,10,6,8)
= Nt
3
t
2
,
where Nt
3
t
2
∈ [17].
There exist {n ∈ N|N(t
1
t
7
)
n
= Nt
3
t
2
}.
Thus, N(t
1
t
7
)
(1,3,9,5)(2,7)(4,10,6,8)
= Nt
3
t
2
.

24
[1236] = [17]
Therefore, Nt
1
t
2
t
3
t
6
N is not a new double coset and collapses ⇒ two symmetric
genertators will take to [17]. Please see the Cayley diagram below.
Figure 1.8: The Cayley Diagram of
3
∗
5
:
m
S
5
[xt]
5
The set of right cosets is closed under right multiplication by t
0
i
s where i =
1, 2, 3, . . . , 10 . Thus, we can determine the index of N in G. We conclude that
|G| ≤ (|N| +
|N|
|N
(1)
|
+
|N|
|N
(12)
|
+
|N|
|N
(17)
|
+
|N|
|N
(123)
|
) × |N|
|G| ≤ (1 + 10 + 20 + 20 + 30) × 120
|G| ≤ (81 × 120) = 9720.
Next, we consider that G = 3
∗
5
:
m
S
5
=< t
1
, x, y > acts on the 81 cosets above
and the actions of t, x, y on the 81 cosets is well-defined. Thus, we have a ho-
momorphism f : G −→ S
81
. Then, f(G) =< f(x), f(y), f(t) >; that is, the
homomorphic image of 3
∗
5
:
m
S
5
is of the order, | < f(x), f(t) > | = 120. Since t

25
has exactly 10 conjugates, we have f(G)
∼
=
< f(x), f(y), f(t) >, where
f(x) =(2, 4, 8, 15, 6)(3, 5, 11, 18, 7)(9, 22, 42, 29, 14)(10, 23, 44, 35, 17)(12, 26, 49, 33, 16)
(13, 27, 52, 39, 19)(20, 40, 55, 30, 38)(21, 41, 65, 36, 32)(24, 47, 56, 31, 34)
(25, 48, 66, 37, 28)(43, 58, 46, 63, 57)(45, 73, 70, 59, 67)(50, 60, 62, 53, 61)
(51, 79, 74, 64, 54)(68, 75, 71, 72, 80)(69, 78, 77, 81, 76).
f(y) =(2, 5)(3, 4)(6, 7)(8, 11)(9, 13)(14, 28)(15, 18)(16, 32)(17, 34)(19, 38)(20, 27)
(21, 26)(22, 25)(23, 24)(29, 39)(30, 48)(31, 47)(33, 35)(36, 41)(37, 40)(42, 52)
(43, 51)(44, 49)(45, 53)(46, 50)(54, 61)(55, 66)(56, 65)(57, 62)(58, 67)(59, 80)
(60, 72)(63, 77)(64, 81)(68, 75)(69, 76)(70, 74)(71, 79)(73, 78).
f(t) =(1, 2, 3)(4, 9, 10)(5, 12, 13)(6, 14, 16)(7, 17, 19)(8, 20, 21)(11, 24, 25)(15, 30, 31)
(18, 36, 37)(22, 39, 43)(23, 45, 46)(26, 50, 51)(27, 53, 29)(28, 54, 42)(32, 57, 58)
(33, 59, 60)(34, 61, 62)(35, 63, 64)(38, 52, 67)(40, 66, 68)(41, 69, 70)(44, 71, 72)
(47, 74, 75)(48, 76, 55)(49, 77, 78)(56, 80, 73)(65, 79, 81).
Next, we will show that 3
4
: S
5
is a homomorphic image of G =
3
∗
5
:
m
S
5
[xt]
5
.
The composition series of G is given by
G = G ⊇ G
1
⊇ G
2
⊇ G
3
⊇ G
4
⊇ G
5
⊇ 1,
where
G = (G/G
1
)(G
1
/G
2
)(G
2
/G
3
)(G
3
/G
4
)(G
4
/G
5
)(G
5
/1) = C
2
A
5
C
3
C
3
C
3
C
3
.
The normal lattice of G is

26
Figure 1.9: The Normal Lattice of G
∼
=
3
4
: S
5
Since the center of G is of order 1, G is not a central extension. The minimal
normal subgroup is of order 81 confirm that we have an abelian subgroup of order
81.
> X:=AbelianGroup(GrpPerm,[3,3,3,3]);
> s:=IsIsomorphic(X,NL[2]);
> s;
true
The above loop prove that [2]=G
2
∼
=
3
4
. Now, we factor G by G
2
such that
G/G
2
∼
=
q to determine the isomporphic type of q.
> q,ff:=quo<G1|NL[2]>;
> s:=IsIsomorphic(q,Sym(5));
> s;
true
We established that q
∼
=
S
5
and the presentation for q is
< a, b|a
5
, b
2
, (ab)
4
, (a, b)
3
> .
Now, we have to find the transversal of q to store its generators and find the action
of its elements on the generators of [2]=G
2
.
> T:=Transversal(G1,NL[2]);
> a:=T[2];
> b:=T[3];
> x:=NL[2].2; y:=NL[2].3; z:=NL[2].4; w:=NL[2].5;
27
Thus, the symmetric presentation for G is
H =< x, y, z, w, a, b|x
3
, y
3
, z
3
, w
3
, (x, y), (x, z), (x, w), (y, z), (y, w), (z, w), a
5
, b
2
, (ab)
4
,
(a, b)
3
, x
a
= y, x
b
= x, y
a
= z, y
b
= x
2
y
2
, z
a
= w, z
b
= z
2
, w
a
= x
2
y
2
z
2
w
2
, w
b
= w
2
>
Next, we want to show that H
∼
=
G.
> f1,H1,k1:=CosetAction(H,sub<H|Id(H)>);
> s:=IsIsomorphic(H1,G1);
> s;
true
Hence, G
∼
=
3
4
: S
5
.
For more examples, please read chapter 3.
In chapter 2, we will state some important definitions and theorems that are related to
our research. In chapter 3, we will use the double coset enumeration (DCE) technique
to construct the Cayley graph, then we will solve the extension problems for the finite
group G. Chapter 4 will illustrate some methods for obtainning homomorphic images
for the progenitor m
∗
n
: N, where m = 2, 3, 5, . . .. In chapter 5, we want to write the
progenitor 2
∗
n
: N when the control subgroup N is a transitive. In chapter 6, we will
construct two interesting groups by using the wreath product process. In chapter 7, we
will write the monomial progenitor p
∗
n
: N, where p is prime, and find its homomorphic
images by factoring the progenitors by suitable relations. In chapter 8, we will state
some facts about the Schur multiplier and universal covering groups. In chapter 9, we
continue working on finding more involutory and non-involutory progenitors.
28
Chapter 2
Preliminaries
In this chapter, we will list all definitions and theorems that are related to our
research on group theory, and we will give a short example to illustrate them.
2.1 Group Theory Preliminaries
Definition 2.1 (Permutation). If X is a nonempty set, a permutation of X is a
bijection φ : X → X.
Note 2.2. The set of all permutations of X is a symmetric group denoted by S
X
.
Example 2.3. let α ∈ S
4
, where α = (1234).There is a bijection from S
4
onto S
4
,
where X = {1, 2, 3, 4} such that
α(1) = 2, α(2) = 3, α(3) = 4, and α(4) = 1.
α =
1 2 3 4
2 3 4 1
Definition 2.4 (Disjoint). Two permutations α, β ∈ S
X
are disjoint if every x moved
by one is fixed by the other. In symbols,
if α(a) 6= a, then β(a) = a, and if α(b) = b, then β(b) 6= b.

29
Example 2.5. Let α, β ∈ S
6
, where α = (12)(34) and β = (56). α and β are disjoint
because
α(5) = 5, but β(5) = 6.
Theorem 2.6 (Rotman). Let α ∈ S
X
. α is either a cycle or a product of disjoint
cycles.
Definition 2.7 (Transposition). A permutation is said to be transposition if it
exchanges two elements and fixes the rest.
Example 2.8. α = (12) ∈ S
3
is a transposition since it fixes 3 and send 1 to 2 and 2
to 1.
Definition 2.9 (Symmetric Group S
n
). S
n
is a symmetric group that formed by
all bijective mapping φ : X → X, where X is a nonempty set.
Definition 2.10 (Alternating Group A
n
). The alternating group A
n
is a subgroup
of S
n
with order equal to
n!
2
.
Definition 2.11 (Abelian Group). A group G is abelian if every pair a, b ∈ G
commutes such as a ∗ b = b ∗ a.
Example 2.12. Let G = A
3
= {e, (123), (132)}. G is abelian group since every pairs
of its distinct elements commutes such that
(123)(132) =e = (132)(123)
e(123) = (123) = (123)e
e(132) = (132) = (132)e
Definition 2.13 (Order of Permutation). Let α = (x
1
, . . . , x
i
)(x
1
, . . . , x
j
) ∈ S
X
,
where α is a multiple of two disjoint cyclic. The order of α is the least common multiple
of the i-cycle and j-cycle.
|α| = lcm(i, j).
Example 2.14. Let α = (123)(45), and β = (12)(3456).
α has two cycles in length 3 and 2. Thus, the order of α is given by
30
|α| = lcm(3, 2) = 6.
β has two cycles in length 2 and 4. Thus, the order of β is given by
|α| = lcm(2, 4) = 4.
Definition 2.15 (Homomorphism). Let G and H be groups. A map φ : G → H is
said to be homomorphism if
for α, β ∈ G, φ(αβ) = φ(α)φ(β)
Note 2.16. If a homomorphism φ from G onto H is a bijection, φ is an isomorphism
function. So, G is isomorphic to H (G
∼
=
H).
Definition 2.17 (Subgroup). A nonempty subset H of a group G is a subgroup of
G if
1. h ∈ H implies h
−1
∈ H.
2. h, k ∈ H imply hk ∈ H.
A subgroup H of G denoted by H ≤ G.
Note 2.18. • A proper subgroup H is any subgroup other than G.
• A trivial subgroup H is the subgroup that generated by the identity.
Example 2.19. Let H = A
3
and G = S
3
.
H is a proper subgroup of G.
• Since e,(123), and (132) are in A
3
, there inverses e,(132),and (123), respectively,
are also in A
3
.
• The product of any two distinct elements of A
3
is in A
3
.
Thus, A
3
≤ S
3
.
Definition 2.20 (Cyclic Subgroup Generated by an element). If G is a group
and a ∈ G, then the cyclic subgroup generated by a, denoted by < a >, is the set of
all powers of a.

31
Definition 2.21 (Order of Group). If G is a group and a ∈ G, then the order of a
is | < a > |, the number of elements in < a >.
Example 2.22. Let
G = S
3
= {e, (12), (13), (23), (123), (132)} and H = A
3
= {e, (123), (132)}.
H ≤ G:
Let h
1
= (123) and h
2
= (132).
1. h
1
= (123) ∈ S
3
implies h
−1
1
= (123)
−1
= (132) ∈ G.
2. h
1
, h
2
∈ S
3
imply h
1
h
2
= e ∈ S
3
.
G = S
3
is generated by a cyclic subgroup (123) and (12). So, S
3
=< (123), (12) >.
|S
3
| = 6.
H = A
3
is generated by a cyclic subgroup (123). So, A
3
=< (123) >. |A
3
| = 3.
Note 2.23. In general, |S
n
| = n! and |A
n
| =
n!
2
for every n ≥ 2.
Definition 2.24 (Right Coset). Let H ≤ G and k ∈ G. The subset of G
Hk = {hk : h ∈ H}
is the right coset of H in G.
Note 2.25. k is called a representative of Hk.
Definition 2.26 (Index). The index of a subgroup H in G is given by
[G : H] =
|G|
|H|
= the number of right cosets of H in G.
Example 2.27. Let G = S
3
, and H = {e, (13)}. The right coset of H in G are
• He = {e, (13)}.
• H(12) = {(12), (132)}.
• H(23) = {(23), (123)}.
G = He ∪ H(12) ∪ H(23) = union of single cosets. The index of H in G is
[S
3
: H] =
|S
3
|
|H|
= 3 =the number of right cosets of H in G.
32
Definition 2.28 (Double Coset). Let H ≤ G and g ∈ G. The double coset of G is
HgH = {Hgh|h ∈ H}.
Note 2.29. Double cosets are composed of single cosets.
Example 2.30 (continued with EX2.25). The double coset of H in G are
• HeH = {Heh|h ∈ H} = {H}.
• H(13)H = {H(13)h|h ∈ H} = {(13), e} = {H}.
• H(12)H = {H(12)h|h ∈ H} = {(12), (123)} = H(123)H.
• H(23)H = {H(23)h|h ∈ H}} = {(23), (132)} = H(132).
G = HeH ∪ H(12)H ∪ H(23)H = union of double cosets.
Theorem 2.31 (Lagrange). If G is a finite group and H ≤ G, then |H| divides |G|
and [G : H] = |G|/|H|.
Definition 2.32 (Exponent). A group G has exponent n if g
n
= 1, for all g ∈ G,
Definition 2.33 (Normal Subgroup). A subgroup H ≤ G is normal in G, denoted
by H G, if
g
−1
Hg = H, for every g ∈ G
Example 2.34. Let H = {e, (12)} ≤ S
3
.
Let h = (12). Then,
h
g
= (12)
(23)
g
−1
hg = (23)
−1
(12)(23)
= (13) /∈ H.
H is not normal in S
3
.
Definition 2.35 (Conjugate). If a ∈ G, then a conjugate of g in G is an element of
the form a
−1
ga for some a ∈ G.
33
Example 2.36. Let G = S
3
, and a = (12), g = (123) are in G. The conjugate of (123)
in S
3
is
(123)
(12)
= (12)
−1
(123)(12)
(213) = (12)(123)(12)
(213) = (132).
Theorem 2.37 (Quotient Group). If H G, then the cosets H in G form a group
G/H of order [G : H].
Definition 2.38 (Commutator). If g, h ∈ G, the commutator of g and h, denoted
by [g, h], is
[g, h] = ghg
−1
h
−1
Definition 2.39 (Derived Subgroup). The derived subgroup of G, denoted by
´
G,
is the subgroup of G generated by all the commutators.
Theorem 2.40 (First Isomorphism Theprem (F.I.T)). Let φ : G → H be a
homomorphism with kerφ. Then
• kerφ G.
• G/kerφ
∼
=
imφ
Theorem 2.41 (Second Isomorphism Theprem (S.I.T)). Let H, K ≤ G and HG.
Then
• H ∩ K K.
• K/H ∩ K
∼
=
HK/H.
Theorem 2.42 (Third Isomorphism Theprem (T.I.T)). Let K ≤ H ≤ G, where
both H and K are normal subgroups of G. Then
G/K/H/K
∼
=
G/H.
Theorem 2.43. Let H ≤ G. H is a maximal normal subgroup of G if there is no
normal subgroup K of G with H < K < G.
34
Definition 2.44 (Simple). Let G 6= 1. A group G is simple if it has no normal
subgroups other than G and 1.
Example 2.45. A
n
, where n ≥ 5 is simple.
Example 2.46. A
4
= h(1234), (12)i is not simple since it has a normal subgroup V
4
=
h(12)(34), (13)(24)i.
Theorem 2.47 (Feit-Thoupson). Every simple group is generated by invalution (el-
ement of order 2).
Definition 2.48 (p-group). A group G is a p-group if the order of every element of
G is a power of p.
Note 2.49. If |G| = p
2
, then G is an abelian group.
If |G| = p
k
, then the center of G is greater than 1. Thus, Z(G) is non-trivial, so
|Z(G)| = p
m
, where 1 ≤ m ≤ k.
Definition 2.50 (Sylow p-subgroup). Let |G| = p
k
m and gcd(p, m) = 1. Then, a
Sylow p-subgroup is of order p
k
.
Example 2.51. |A
5
| = 2
2
.3.5. A
5
have Sylow 2-subgroups since gcd(2, 3, 5) = 1.
Definition 2.52 (Elementry Abelian Group). . Let G be a finite group. it said to
be elementry abelian group if it is abelian such that every nontrivial element a ∈ G
has a prime order p. The general presentation for this group is given by
(Z/pZ)
n
∼
=
< a
1
, ..., a
n
|a
p
i
= 1, a
i
a
j
= a
j
a
i
>
Definition 2.53 (Stabiliser). The stabiliser of w in N is given by
N
w
= {n ∈ N|w
n
= w}, where w is a word of t
i
0
s.
Definition 2.54 (Coset Stabiliser). The coset stabiliser of Nw in N is given by
N
(w)
= {n ∈ N|Nw
n
= Nw}, where w is a word of t
i
0
s.
Note 2.55. N
w
≤ N
(w)
.
Example 2.56. Let G = S
3
. Then N
1
= {e, (23)} = N
(1)
.
35
Definition 2.57 (G-set). If X is a set and G is a group, then X is a G-set if there is
a function φ : G × X → X, denoted by φ : (g, x) → gx, such that:
1. 1x = x for all x ∈ X.
2. gh(x) = (gh)x for all g, h ∈ G and x ∈ X.
Definition 2.58 (Direct Product (H × K)). Let G be a group and H, K ≤ G. G is
a direct product of H and K if
1. H, K G.
2. G = HK.
3. H ∩ K = 1.
Example 2.59. Let G = V
4
= ha, b|a
2
= b
2
= (ab)
2
= 1i = {e, a, b, ab}, H = {e, a},
and K = {e, b}.
Note:
(ab)
2
= 1 ⇒ abab = 1
aba = b
−1
ab = b
−1
a
−1
ab = (ab)
−1
.
• H, K G because
H
e
= {e
e
, a
e
} = {e, a} ∈ V
4
.
H
a
= {e
a
, a
a
} = {e, a} ∈ V
4
.
H
b
= {e
b
, a
b
} = {e, b
−1
ab = bab} = {e, a} ∈ V
4
.
H
ab
= {e
ab
, a
ab
} = {e, (ab)
−1
a(ab)} = {e, a} ∈ V
4
.
Similiarely for K.
• H ∩ K = {e, a} ∩ {e, b} = {e}.
• HK = {e, a, b, ab} = V
4
Hence, V
4
is a direct product of H by K, denoted by H × K.
Theorem 2.60. Let G be a group with normal subgroups H and K. If
36
• HK = G
• H ∩ K = 1.
Then G
∼
=
H × K.
Example 2.61. Let G = hai and |a| = 4.
G = HK. If |G| = |H|, then |H| = 2 = |K|. But, G has only ha
2
i = {e, a
2
} = H as a
normal subgroup of order 2.
There does not exist K ≤ G 3 |K| = 2; H ∩ K = 1.
G is not a direct product.
Definition 2.62 (Complement). Let K be a (not necessarily normal) subgroup of a
group G. Then a supgroup Q ≤ G is a complement of K in G if
1. KQ = G.
2. K ∩ Q = 1.
Example 2.63. Let G = S
3
and K = A
3
= {e, (123), (132)}. K has 3 complements in
S
3
such as
{e, (12)}, {e, (13)}, and {e, (23)}.
⇒ S
3
= QK, where Q = {e, (12), (13), (23)} ≤ S
3
.
Example 2.64. Let G = hai and |a| = 4.
H = {1, a
2
} does not have a complement in G since there is not a normal subgrops of
order 2.
This example showed that a complement does not always exist.
Definition 2.65 (Semi-direct Product). A group G is a semi-direct product of K
by Q, denoted by G = K : Q, if K G and K has a complement Q
1
∼
=
Q.
Example 2.66. Since H = {e, (12)} is a complement of A
3
in S
3
(shown in Ex 2.55)
isomorphic to Z
2
. S
3
is a semi-direct product of A
3
by Z
2
, denoted by S
3
= A
3
: Z
2
.
Definition 2.67. Let G be a group, and H and K are normal subgroups of G. Then
G
∼
=
H × K if
37
1. HK = G
2. H ∩ K = 1
Definition 2.68 (Center). Let G be a group. The center of G, denoted by (Z(G)),
is the set of all a ∈ G that commute with every element of G.
Example 2.69. Let G = S
3
. Since the identity is the onley permutation that commutes
with all g ∈ S
3
, Z(G) = {e}.
Let G = A
3
. Z(G) = {g
a
= g|a ∈ G} = {(123)}.
Definition 2.70 (Centralizer). If a ∈ G, then the centralizer of a in G, denoted by
C
G
(a), is the set of all x ∈ G which commute with a.
C
G
(a) = {a
x
= a|x ∈ G}.
Example 2.71. Let G = A
3
. We want to find the centraliser of a = (123) ∈ A
3
.
(123)e = (123) = e(123)
(123)(123) = (132) = (123)(123)
(123)(132) = e = (132)(123)
Thus, C
A
3
((123)) = {e, (123), (132)} = A
3
Theorem 2.72 (Rotman). If a ∈ G, the number of conjugates of a is equal to the index
of its centralizer.
|a
G
| = [G : C
G
(a)].
Example 2.73. |(123)
A
3
| = [A
3
: A
3
] = 1.
Definition 2.74 (Normaliser). If H ≤ G, then the normalizer of H in G is defined
by
N
G
(H) = {a ∈ G|aHa
−1
= H}.
Definition 2.75 (Conjugacy Class). Let G be a group and a ∈ G. The conjugacy
class of a is
a
G
= {a
g
|g ∈ G} = {g
−1
ag|g ∈ G}
38
Example 2.76. Let G = A
4
.
The conjugacy classes of (12)(34) ∈ A
4
is the set
(12)(34)
G
= {(12)(34), (13)(24), (14)(23)}.
Definition 2.77 (G-Orbit). Let x ∈ X. The set X
G
= {x
g
|g ∈ G} is the G-Orbit.
Example 2.78. Let G = A
3
and X = {1, 2, 3} be a G-set.
1
G
= {1
e
, 1
(123)
, 1
(132)
} = {1, 2, 3} = 2
G
= 3
G
since 2, 3 ∈ 1
G
.
The G-Orbit X
G
is {1,2,3}.
Definition 2.79 (Faithful). A G-set X with action α is faithful if ˜α : G → S
X
is
injective.
Definition 2.80 (k-transitive). Let X be a G-set of degree n and let k ≤ n be a positive
integer. Then X is k-transitive if there is g ∈ G with gx
i
= y
i
for i = 1, . . . , k.
Note 2.81. S
n
is n-transitive, and A
n
is (n − 2)-transitive.
Example 2.82. Let G = S
3
. Then
• X = {1, 2, 3}.
• The orbit of 2 is 2
G
= {2
g
|g ∈ G} = {1, 2, 3}.
• G is a 3-transitive on X.
Example 2.83. Let G = A
4
, H = {1, (123), (132)}.
Since 1
H
= {1
h
: h ∈ H} = {1, 2, 3} and 4 takes to 4 by the identity, H is not transitive
on {1,2,3,4}.
H is not a 4-transitive.
Definition 2.84 (Sharply k-transitive). A k-transitive G-set X is Sharply k-
transitive if only the identity fixes k distinct elements of X.
Definition 2.85 (Dihedral Group). The dihedral group D
2n
is a group generated
by two elements a and b with presentation
< a, b|a
n
= b
2
= (ab)
2
= 1 > .
The order of D
2n
is equal to 2n, where 2n ≥ 4.
39
Example 2.86. D
10
= D
2(5)
=< a, b|a
5
= b
2
= (ab)
2
= 1 >. The order of D
10
is equql
to 10.
Definition 2.87 (Quaternion Group). The quaternion group Q is a group gener-
ated by two elements a and b with presentation
< a, b|a
2n
= b
4
= 1, a
n
= b
2
, b
−1
ab = a
−1
> .
Example 2.88. Q
8
=< a, b|a
4
, b
4
, aba = b, a
2
= b
2
>. The order of Q
8
is equal to 8 .
Definition 2.89 (Normal Series). A chain of subgroup of G
G
0
= G ⊇ G
1
⊇ . . . ⊇ G
n
= 1 3 G
i
G ∀1 ≤ i ≤ n
is called a normal series of G.
Example 2.90. Consider D
4
= ha, b|a
4
= b
2
= (ab)
2
= 1i = {e, a, a
2
, a
3
, b, ab, a
2
b, a
3
b}.
G = G
0
= D
4
, G
1
=< a >, G
2
=< a
2
>, G
3
= 1.
D
4
⊇< a >⊇< a
2
>⊇ 1
is a normal series of D
4
.
Note 2.91. A normal series is a chief series (cannot add any more groups to the chain).
Definition 2.92 (Subnormal Series). A chain of subgroup of G
G
0
= G ⊇ G
1
⊇ . . . ⊇ G
n
= 1 3 G
i+1
G
i
, for all 0 ≤ i ≤ n − 1
is called a subnormal series of G.
Example 2.93. S
4
⊇ A
4
⊇ 1 is a subnormal series of S
4
.
Note 2.94. We can add another group to the chain without repetition.
Example 2.95. S
4
⊇ A
4
⊇ V
4
⊇ 1
Definition 2.96. SL(n, F) is aspecial linear of n × n matrices over finite field F with
determinant equal to 1.
Example 2.97.
SL(2, R) =
a b
c d
: a, b, c, d ∈ R, ad − bc = 1 or a square
40
Definition 2.98. GL(n, F) is ageneral linear group of n × n matrices over finite field
F..
Example 2.99.
GL(2, R) =
a b
c d
: a, b, c, d ∈ R, ad − bc 6= 0
Definition 2.100. P SL(n, F) is aprojective special linear group of n × n matrices
over finite field F that formed by factoring SL by its center.
P SL(n, F) = L
n
(F) = SL(n, F)/Z(SL(n, F)).
Definition 2.101. P GL(n, F) is aprojective general linear group of n × n matrices
over finite field F that formed by factoring GL by its center.
P GL(n, F) = GL(n, F)/Z(GL(n, F)).
Definition 2.102 (Minimal Normal Subgroup). A Minimal Normal Subgroup
N of G is a direct product of simple groups.
Note 2.103. If N is a minimal p-subgroup then N is a direct product of elementry
p-subgroups
Example 2.104. Let N be a minimal normal subgroup of order 4. Then, N
∼
=
2 × 2.
2.2 Group Extension Preliminaries
Definition 2.105 (Group Extensions). An extension of a group N by a group H is
a group G with a normal subgroup M such that M
∼
=
N and G/M
∼
=
H.
Example 2.106. Let G = Z
6
. G is an extension of Z
2
by Z
3
.
Z
6
=< a >= {e, a, a
2
, a
3
, a
4
, a
5
}, |a| = 6.
Z
2
=< a
3
>= {e, a
3
}.
Z
6
/Z
2
= < a >/< a
3
>
= {{e, a
3
}, a{e, a
3
}, a
2
{e, a
3
}}
=< a{e, a
3
} > .
Z
6
/Z
2
∼
=
Z
3
.
41
Example 2.107. Let G = S
3
= ha, b|a
3
, b
2
, (ab)
2
i. S
3
is not an extension of Z
2
by
Z
3
because it does not have a normal subgroup of order 2. Thus, H
1
= {e, (12)},
H
2
= {e, (13)}, and H
3
= {e, (23)} are subgroups of order 2 but none of them is
normal.
h(123)i = {e, (123), (132)}.
S
3
/h(123)i = {h(123)i, (12)h(123)i}
S
3
/h(123)i
∼
=
Z
2
S
3
/Z
3
∼
=
Z
2
.
Hence, S
3
is an extension of Z
3
by Z
2
.
Note 2.108. The previous two examples showed that the composition series of a group
G is not unique. Thus, S
3
Z
6
.
Given groups H and N there are many extensions of N by H such as
1. Direct product extension.
2. Semi-direct product extension.
3. Central extension.
4. Mixed extension.
We have defined the first two extensions in page 26-27.
Definition 2.109 (Central Extensions N
•
H). N is the center of G if G is a central
extension of N by H. It is based on Ψ : H × H −→ N .
All elements of N commute with all the elements of G (N is abelian). The group
operation of G = N ↑ H is
(n
1
, h
1
) ∗ (n
2
, h
2
) = (n
1
∗ n
2
∗ ψ(h
1
, h
2
), h
1
h
2
).
Example 2.110. Let a group G has the following composition series G = G
1
⊇ G
2
,
where G = (G
1
/G
2
) = (G
1
/1) = G
1
= C
3
A
7
= NH and A
7
= h(123), (234567)i.
Since the center of G is Z(G) = {g
a
= g|a ∈ G} = {(123)} = N, this is a central
extension of C
3
by A
7
denoted by 3
•
A
7
.
42
Example 2.111. Let a group G = D
4
= {a
4
, b
2
, (ab)
2
} = {1, a, a
2
, a
3
, b, ab, a
2
b, a
3
, b}.
D
4
is either a central or a direct product extension. The normal lattice of D
4
is
[1]=e
↓
[2]={1, a
2
}
. &
{1, a
2
, b, a
2
b}=[3] [4]={1, a, a
2
, a
3
}
& .
[5]=D
4
D
4
has 2 normal subgroups of order 4. Thus,
D
4
∼
=
[2] × [3], but [2] ∩ [3] 6= 1.
D
4
∼
=
[2] × [4], but [2] ∩ [4] 6= 1.
So, D
4
is must be a central extension 2
•
(C
2
× C
2
) = 2
•
C
4
,
Where
D
4
/Z(D
4
) = D
4
/{1, a
2
}
= {{1, a
2
}, a{1, a
2
}, b{1, a
2
}, ab{1, a
2
}}
= C
4
Therefore,
D
4
/Z(D
4
)
∼
=
C
4
⇒ D
4
∼
=
2
•
C
4
Definition 2.112 (Mixed Extensions N • H). It is combined the properties of a
semi-direct product and a central extension. N is a normal subgroup, but it is not a
central.
∃Φ : H −→ Aut(N) and Ψ : H × H −→ N. The group operation of G is
(n
1
, h
1
) ∗ (n
2
, h
2
) = (n
1
∗ h
h1
2
∗ ψ(h
1
, h
2
), h
1
h
2
).
Example 2.113. Let G has the following composition series G = C
2
C
2
C
2
A
5
= Q
8
A
5
.
43
• G Q
8
× A
5
because G does not have a normal subgroup of order 60.
• G Q
8
: A
5
because A
5
≤ Aut(Q
8
) = S
4
.
• G Q
•
8
A
5
because Z(G) 6= Q
8
.
Thus, G is a mixed extension of Q
8
by A
5
denoted by G
∼
=
Q
8
• A
5

44
Chapter 3
Double Coset Enumeration and
Composition Factors
The objective of this chapter is to find the index of N in G = p
∗
n
: N , where
G is a semi-direct product of a free product p
∗
n
of n cyclic groups of order p by the
control group N. G = p
∗
n
: N is called a progenitor. Since G is infinite group,
we must add one or more relations of the form π
i
ω
i
in order to form a finite group
G =
p
∗
n
:N
π
i
ω
i
. To construct these finite groups, we will use the double coset enumeration
(DCE) technique. Thus, we need to express G as a union of double cosets N gN , where
g is an element of G. Thus, G = N eN
S
Ng
1
N
S
Ng
2
N
S
. . ., where g
i
0
s are words in
t
i
0
s. Now, we need to find out all [w] = {N w
n
|n ∈ N}, which are the double cosets,
and how many single cosets each of them contains. The our desired result of DCE is
complete when the set of right cosets is closed under right multiplication by t
i
0
s.
In this chapter, we will consider the progenitor 2
∗
4
: A
4
. Then, this progenitor will
factored by approbriate relations to give this homomorphic images S
5
, L
2
(11) × 3, and
L
2
(11). Similarily, we will consider the progenitor 2
∗
5
: D
10
, then we will factore it by
suitable relations to give the homomorphic image P GL
2
(11). We have discoverd several
homomorphic images that all listed in a table at the end of the chapter.
Note 3.1. G = 2
∗
n
: N is called an involutory progenitor.

45
3.1 S
5
as a Homomorphic Image of 2
∗
4
: A
4
3.1.1 The Construction of S
5
over A
4
Consider the group G = hx, y, t|x
2
, y
3
, (xy)
3
, t
2
, (t, y)i factored by [y
2
xtt
x
]
2
and
[ytt
x
t
x
2
]
4
, where G = 2
∗
4
: A
4
, N = A
4
= hx, yi = h(12)(34), (123)i, and let t = t
4
. So,
(y
2
xtt
x
)
2
= e
(y
2
x(t
4
t
3
)
y
2
x
(t
4
t
3
) = e
((y
2
)x)
2
t
3
t
1
t
4
t
3
= e
(134)t
4
t
3
t
4
t
3
t
4
= e
(134)t
3
t
1
= t
3
t
4
⇒ Nt
3
t
1
= Nt
3
t
4
(ytt
x
t
x
2
)
4
= e
(yt
4
t
3
t
4
)
4
= e
y
4
(t
4
t
3
t
4
)
y
3
(t
4
t
3
t
4
)
y
3
(t
4
t
3
t
4
)
y
2
(t
4
t
3
t
4
)
y
(t
4
t
3
t
4
) = e
y(t
4
t
3
t
4
)(t
4
t
2
t
4
)(t
4
t
1
t
4
)(t
4
t
3
t
4
) = e
yt
4
t
3
t
2
t
1
t
3
t
4
= e ⇒ Nt
4
t
3
t
2
= Nt
4
t
3
t
1
.
Moreover, if we conjugate the previous relation by all elements in A
4
, we obtain:
(243)t
4
t
2
= t
4
t
3
, (421)t
2
t
4
= t
2
t
1
,
(413)t
1
t
4
= t
1
t
3
, (142)t
4
t
1
= t
4
t
2
,
(231)t
3
t
2
= t
3
t
1
, (324)t
2
t
3
= t
2
t
4
,
(341)t
4
t
3
= t
4
t
1
, (432)t
3
t
4
= t
3
t
2
,
(123)t
2
t
1
= t
2
t
3
, (214)t
1
t
2
= t
1
t
4
,
(312)t
1
t
3
= t
1
t
2
.
Thus, we have the following equivelent cosets. Let t = t
4
→ t
0
.
31 ≈ 30 ≈ 32,
23 ≈ 20 ≈ 21,
12 ≈ 10 ≈ 13, and
03 ≈ 01 ≈ 02.
The main goal of this example is to show that G =
2
∗
4
:A
4
(134)t
3
t
1
=t
3
t
0
∼
=
S
5
. First, we start
with the double coset N eN, denoted by [∗], which consists of the single coset N. Then,

46
we consider the double coset N wN, where w is a word of length one and so on until the
set of right cosets is closed under right multiplication by t
0
i
s where i = 0, · · · , 3.
• Consider N eN, denoted by [∗].
NeN = {N}.
The number of right cosets in [∗] is equal to
|N|
|N|
=
12
12
= 1.
Since N is a transitive on {0,1,2,3}, the orbit of N is {0,1,2,3}.
Pick a representative from the orbit {0,1,2,3}, say t
0
, and determine the double
coset that contain Nt
0
.
Word of length 1.
• Consider N t
0
N denoted by [0].
N
0
= h(123), (132)i = N
(0)
.
The number of right cosets in [0] is equal to
|N|
|N
(0)
|
=
12
3
= 4.
The orbits of N
(0)
on {0,1,2,3} are {0} and {1,2,3}.
Pick a representative from each orbit, say t
0
and t
1
respectivelly, and determine
the double cosets that contain N t
0
t
0
and Nt
0
t
1
.
Nt
0
t
0
∈ [∗] (1 symmetric generator goes back to the double coset [∗]).
Nt
0
t
1
∈ [01] (3 symmetric generators take to the double coset [01]).
Word of length 2.
• Consider N t
0
t
1
N denoted by [01].
N
01
= hei. The right cosets in [01] are not distinct. From above relations, we see
that
01 ≈ 02 ≈ 03 ⇒ Nt
0
t
1
= Nt
0
t
2
= Nt
0
t
3
Thus, there exist {n ∈ N|N(t
0
t
1
)
n
= Nt
0
t
1
} such that
N(t
0
t
1
)
(123)
= Nt
0
t
2
relation
= Nt
0
t
1
⇒ (123) ∈ N
(01)
N(t
0
t
1
)
(132)
= Nt
0
t
3
relation
= Nt
0
t
1
⇒ (132) ∈ N
(01)
So, N
(01)
= h(123)i.
The number of right cosets in [01] is equal to
|N|
|N
(01)
|
=
12
3
= 4.
47
The orbits of N
(01)
on {0,1,2,3} are {0} and {1,2,3}.
Nt
0
t
1
t
0
∈ [010] (1 symmetric generator go to the double coset [010]).
Nt
0
t
1
t
1
= Nt
0
∈ [0] (3 symmetric generators take bake to the double coset [0]).
Word of length 3.
• Consider N t
0
t
1
t
0
N denoted by [010].
N
010
= hei. From previous relations, we obtain the following
t
0
t
1
t
0
= (301)t
0
t
3
t
0
⇒ Nt
0
t
1
t
0
= Nt
0
t
3
t
0
.
t
0
t
1
t
0
= (120)t
0
t
2
t
0
⇒ Nt
0
t
1
t
0
= Nt
0
t
2
t
0
.
t
0
t
1
t
0
= t
0
(210)t
1
t
2
= (210)t
2
t
1
t
2
⇒ Nt
0
t
1
t
0
= Nt
2
t
1
t
2
.
t
0
t
1
t
0
= t
0
(031)t
1
t
3
= (031)t
3
t
1
t
3
⇒ Nt
0
t
1
t
0
= Nt
3
t
1
t
3
.
t
0
t
1
t
0
= (301)t
0
t
3
t
0
= (301)t
0
(130)t
3
t
1
= (310)t
1
t
3
t
1
⇒ Nt
0
t
1
t
0
= Nt
1
t
3
t
1
.
t
0
t
1
t
0
= (301)t
0
t
3
t
0
= (301)t
0
(023)t
3
t
2
= (32)(10)t
2
t
3
t
2
⇒ Nt
0
t
1
t
0
= Nt
2
t
3
t
2
.
t
0
t
1
t
0
= (120)t
0
t
2
t
0
= (120)t
0
(012)t
2
t
1
= (102)t
1
t
2
t
1
⇒ Nt
0
t
1
t
0
= Nt
1
t
2
t
1
.
t
0
t
1
t
0
= (120)t
0
t
2
t
0
= (120)t
0
(320)t
2
t
3
= (10)(23)t
3
t
2
t
3
⇒ Nt
0
t
1
t
0
= Nt
3
t
2
t
3
.
t
0
t
1
t
0
= (210)t
2
t
1
t
2
= (210)(021)t
2
t
0
t
2
= (201)t
2
t
0
t
2
⇒ Nt
0
t
1
t
0
= Nt
2
t
0
t
2
.
t
0
t
1
t
0
= (031)t
3
t
1
t
3
= (031)(103)t
3
t
0
t
3
= (013)t
3
t
0
t
3
⇒ Nt
0
t
1
t
0
= Nt
3
t
0
t
3
.
t
0
t
1
t
0
= (201)t
2
t
0
t
2
= (201)t
2
(102)t
0
t
1
= t
1
t
0
t
1
⇒ Nt
0
t
1
t
0
= Nt
1
t
0
t
1
.
Hence,
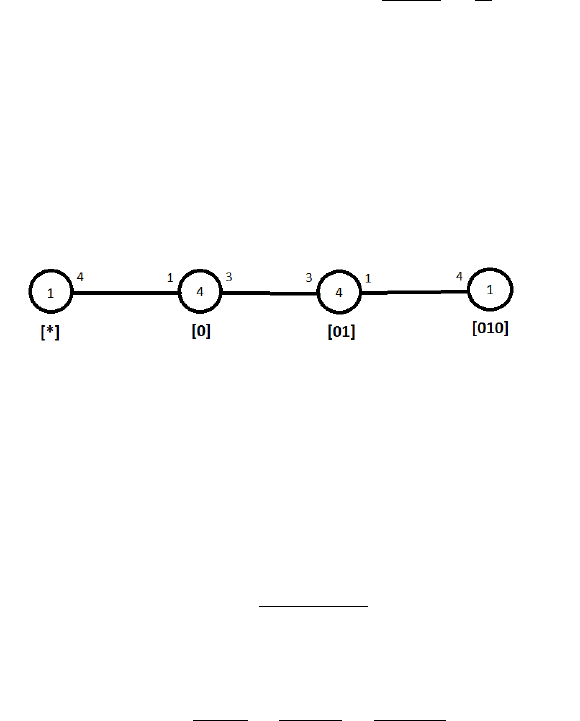
48
t
0
t
1
t
0
≈ t
0
t
3
t
0
≈ t
0
t
2
t
0
≈ t
2
t
1
t
2
≈ t
3
t
1
t
3
≈ t
1
t
3
t
1
≈
t
2
t
3
t
2
≈ t
1
t
2
t
1
≈ t
3
t
2
t
3
≈ t
2
t
0
t
2
≈ t
3
t
0
t
3
≈ t
1
t
0
t
1
Therefore, N
(010)
= {n ∈ N|N(010)
n
= N(010)}.
Thus, N
(010)
≥ h(12)(34), (123)i = A
4
.
The number of right cosets in [010] is equal to
|N|
|N
(010)
|
=
12
12
= 1.
The orbits of N
(010)
on {0,1,2,3} is {0, 1, 2, 3}.
Nt
0
t
1
t
0
t
0
= Nt
0
t
1
(4 symmetric generators go back to the double coset [01]).
Now, we can construct the Cayley diagram of S
5
over A
4
.
Figure 3.1: Cayley Diagram for S
5
Over A
4
Since the set of right cosets is closed under right multiplication by t
0
i
s where i = 0, · · · , 3,
we can determine the index of N in G. We conclude that
G =
2
∗
4
:A
4
(134)t
3
t
1
=t
3
t
0
|G| ≤
|N| +
|N|
|N
(0)
|
+
|N|
|N
(01)
|
+
|N|
|N
(010)
|
× |N |
|G| ≤ (1 + 4 + 4 + 1) × 12
|G| ≤ (10 × 12)
|G| ≤ 120

49
Table 3.1: Single Coset Action of S
5
Over A
4
Label Single Cosets x y t
0
1 N 1 N 1 N 2 N t
0
2 Nt
0
3 N t
3
2 N t
0
1 N
3 Nt
3
2 N t
0
4 N t
1
5 N t
3
t
0
4 Nt
1
6 N t
2
6 N t
2
7 N t
1
t
0
5 Nt
3
t
0
8 N t
0
t
3
7 N t
1
t
0
3 N t
3
6 Nt
2
4 N t
1
3 N t
3
9 N t
2
t
0
7 Nt
1
t
0
9 N t
2
t
3
9 N t
2
t
0
4 N t
1
t
0
t
0
= Nt
1
8 Nt
0
t
3
5 N t
3
t
0
8 N t
0
t
1
10 N t
0
t
3
t
0
9 Nt
2
t
0
7 N t
1
t
3
5 N t
3
t
0
6 N t
2
t
0
t
0
= Nt
2
10 Nt
0
t
1
t
0
10 N t
3
t
2
t
3
10 N t
0
t
2
t
0
8 N t
0
t
1
t
0
t
0
= Nt
0
t
1
We find
f(x) = (23)(46)(58)(79).
f(y) = (346)(579).
f(t) = (12)(35)(47)(69)(8, 10).
Next, we note that G = 2
∗
4
: A
4
=< t
0
, x, y > acts on the ten cosets above and the
actions of t, x, and y on the ten cosets is well-defined. Thus, we have a homomorphism
f : G −→ S
10
. Then f(G) =< f(x), f(y), f(t) >; that is, the homomorphic image of
2
∗
4
: A
4
is of the order, | < f (x), f(y), f(t) > | = 120. Since t has exactly 4 conjugates,
we have f(G)
∼
=
< f(x), f(y), f(t) >.
Hence,
G/Ker
f
∼
=
< f(x), f(y), f(t) >= f(G)
⇒ |G/Ker
f
| = |f(G)|
⇒ |G| = |f(G)| = 120
⇒ |G| = |Ker
f
| ∗ 120
⇒ |G| ≥ 120.
From the Cayley diagram, we observed that |G| ≤ 120 and |Ker
f
| = 1. Hence, Ker
f
= 1
and |G| = 120.
G
∼
=
< f(x), f(y), f(t) >
In the next section, we will show that G
∼
=
S
5
.
50
3.1.2 Proof of the Isomorphism
Consider the group
G =< x, y, t|x
2
, y
3
, (xy)
3
, t
2
, (t, y), (y
2
xtt
x
)
2
, (ytt
x
t
x
2
)
4
> .
By using MAGMA, we have the composition series G ⊇ G
1
⊇ G
2
, where
G = (G/G
1
)(G
1
/G
2
) = (G/G
1
)(G
1
/1) = C
2
A
5
.
Now, we want to determine the extension type of this group.
> CompositionFactors(G1);
G
| Cyclic(2)
*
| Alternating(5)
1
Since the center of G is of order 1, this is not a central extension. Moreover, by looking
at the normal lattice of G, we see that it does not have a normal subgroup of order 2.
Thus, this is not a direct product.
> D:=DirectProduct(NL[2],NL[3]);
> s,t:=IsIsomorphic(D,G1);
> s;
false
We find that it is a semi-direct product. Thus, we have A
5
extended by C
2
. Then,
we must find the action of C
2
on the generators a and b of A
5
.
> H<a,b>:=Group<a,b|aˆ2,bˆ3,(a
*
b)ˆ5>;
> #H;
60
> f1,H1,k1:=CosetAction(H,sub<H|Id(H)>);
> s,t:=IsIsomorphic(H1,NL[2]);
> s;
true
> s,t:=IsIsomorphic(H1,Alt(5));
> s;
true
> a:=NL[2].1;
> b:=NL[2].2;
51
> for g in G1 do if Order(g) eq 2 and g notin NL[2]\
> and G1 eq sub<G1|NL[2],g>\
then U:=g; break; end if; end for;
> G1 eq sub<G1|NL[2],U>;
true
> N:=sub<G1|a,b>;
> #N;
60
By using Schreier System, we compute the action of c on a and b and write a presentation
for A
5
: C
2
.
A:=[Id(NN): i in [1..2]];
for i in [1..60] do
if aˆU eq ArrayP[i] then A[1]:=Sch[i]; Sch[i]; end if; end for;
for i in [1..60] do
if bˆU eq ArrayP[i] then A[2]:=Sch[i]; Sch[i]; end if; end for;
HH<a,b,c>:=Group<a,b,c|aˆ2,bˆ3,(a
*
b)ˆ5,cˆ2,
aˆc=a,bˆc=a
*
bˆ-1
*
a
*
b
*
a
*
bˆ-1>;
#HH;
f2,H2,k:=CosetAction(HH,sub<HH|Id(HH)>);
s:=IsIsomorphic(H2,G1);
> s;
true
At the end, we check if this presentation is isomorphic with S
5
.
> s:=IsIsomorphic(H2,Sym(5));
> s;
true
So, we obtained that G = A
5
: C
2
∼
=
S
5
.
3.2 L
2
(11) × 3 as a Homomorphic Image of 2
∗
4
: A
4
3.2.1 The Construction of L
2
(11) × 3 over A
4
Consider the group
G = 2
∗
4
: A
4
= hx, y, t|x
2
, y
3
, (xy)
3
, (y
−1
x
−1
yx)
2
, t
2
, (t, y)i factored by [xt]
5
.

52
N = A
4
= hx, yi = h(12)(34), (123)i and let t = t
4
. So,
(xt)
5
= e
(xt
4
)
5
= e
x
5
t
4
x
4
t
4
x
3
t
4
x
2
t
4
x
t
4
= e
xt
4
t
3
t
4
t
3
t
4
= e
xt
4
t
3
t
4
= t
4
t
3
(12)(34)t
4
t
3
t
4
= t
4
t
3
.
t
1
= t
x
y
, t
2
= t
1
y
, t
3
= t
x
By conjugatation with all elements in A
4
, we will have the following relations:
(12)(34)t
3
t
4
t
3
= t
3
t
4
, (12)(34)t
4
t
3
t
4
= t
4
t
3
,
(12)(34)t
2
t
1
t
2
= t
2
t
1
, (12)(34)t
1
t
2
t
1
= t
1
t
2
,
(23)(14)t
4
t
1
t
4
= t
4
t
1
, (23)(14)t
1
t
4
t
1
= t
1
t
4
,
(23)(14)t
3
t
2
t
3
= t
3
t
2
, (23)(14)t
2
t
3
t
2
= t
2
t
3
,
(13)(24)t
4
t
2
t
4
= t
4
t
2
, (13)(24)t
1
t
3
t
1
= t
1
t
3
,
(13)(24)t
3
t
1
t
3
= t
3
t
1
, (13)(24)t
2
t
4
t
2
= t
2
t
4
.
The double coset enumeration:
• Consider N eN which is denoted by [∗].
The number of the right cosets in [∗] =
|N|
|N|
=
12
12
= 1.
The orbit of N on{0,1,2,3} is {0,1,2,3}.
Pick a representative from the orbit {0,1,2,3}, say 0, and determine the double
coset that contain Nt
0
.
Word of length 1.
• Consider N t
0
N which is denoted by [0].
N
0
= h(123), (132)i = N
(0)
.
The number of the right cosets in [0] is equal to
|N|
|N
(0)
|
=
12
3
= 4.
The orbit of N
(0)
on{0,1,2,3} are {0} and {1,2,3}.
Nt
0
t
0
∈ [∗] (1 symmetric generator goes back to the double coset [∗]).
Nt
0
t
1
∈ [01] (3 symmetric generators take to the double cose [01]).

53
Word of length 2.
• Consider N t
0
t
1
N which is denoted by [01].
N
01
= hei = N
(01)
.
The number of the right cosets in [01] =
|N|
|N
(01)
|
=
12
1
= 12.
The orbits of N
(01)
on {0,1,2,3} are {0}, {1}, {2}, and {3}.
Nt
0
t
1
t
0
= N(14)(23)t
0
t
1
= Nx
y
t
0
t
1
(1 symmetric generator goes back to the
double coset [01])
Nt
0
t
1
t
1
= Nt
0
(1 symmetric generator goes back to the double coset [0])
Nt
0
t
1
t
2
∈ [012].
Nt
0
t
1
t
3
∈ [013].
Word of length 3.
• Consider N t
0
t
1
t
2
N which is denoted by [012].
N
012
= hei = N
(012)
.
The number of the right cosets in [012] =
|N|
|N
(012)
|
=
12
1
= 12.
The orbits of N
(012)
on {0,1,2,3} are {0}, {1}, {2}, and {3}.
Nt
0
t
1
t
2
t
0
∈ [0120].
Nt
0
t
1
t
2
t
1
∈ [0121].
Nt
0
t
1
t
2
t
2
= Nt
0
t
1
(1 symmetric generator goes back to the double coset [01]).
Nt
0
t
1
t
2
t
3
∈ [0123].
• Consider N t
0
t
1
t
3
N which is denoted by [013].
N
013
= hei = N
(013)
.
The number of the single cosets in [013] =
|N|
|N
(013)
|
=
12
1
= 12.
The orbits of N
(013)
on {0,1,2,3} are {0}, {1}, {2}, and {3}.
Nt
0
t
1
t
3
t
0
∈ [0130].
Nt
0
t
1
t
3
t
1
∈ [0131].
Nt
0
t
1
t
3
t
2
∈ [0132].
Nt
0
t
1
t
3
t
3
= Nt
0
t
1
(1 symmetric generator goes back to the double coset [01])
Word of length 4.
• Consider N t
0
t
1
t
2
t
1
N which is denoted by [0121].

54
Because the relation
Nt
0
t
1
t
2
t
1
= N(12)(34)[t
0
t
1
t
3
]
(432)
= Nxt
3
t
1
t
2
= Nt
3
t
1
t
2
.
where Nt
3
t
1
t
2
∈ [013].
There exist {n ∈ N|N(t
0
t
1
t
3
)
n
= Nt
3
t
1
t
2
}.
Thus, N(t
0
t
1
t
3
)
(432)
= Nt
3
t
1
t
2
.
[0121] = [013]
Therefore, Nt
0
t
1
t
2
t
1
N is not a new double coset and collapses ⇒ 1 takes to [013].
• Consider N t
0
t
1
t
2
t
0
N which is denoted by [0120].
N
0120
= hei. The right cosets in [0120] are not distinct. From above relations, we
see that
t
0
t
1
t
2
t
0
= t
0
t
1
(13)(24)t
2
t
0
t
2
= (13)(24)t
2
t
3
t
2
t
0
t
2
= (13)(24)(23)(14)t
2
t
3
t
2
t
2
t
0
t
2
= (12)(34)t
2
t
3
t
0
t
2
= xt
2
t
3
t
0
t
2
. Thus 0120 ≈ 2302.
Therefore, N
(0120)
= {n ∈ N|N(0120)
n
= N(2302)}.
N(0120)
(13)(24)
= N2302 = N0120 ⇒ (13)(24) ∈ N
(0120)
N
(0120)
≥ h(13)(24)i.
[0120] =
|N|
|N
(0120)
|
=
12
2
= 6.
The orbits of N
(0120)
on {0, 1, 2, 3} are {1, 3} and {0, 2}.
Nt
0
t
1
t
2
t
0
t
1
∈ [01201] (2 symmetric generators take to the double coset [01201]).
Nt
0
t
1
t
2
t
0
t
0
= Nt
0
t
1
t
2
(2 symmetric generators go back to the double coset [012]).

55
• Consider N t
0
t
1
t
2
t
3
N which is denoted by [0123].
N
0123
= hei = N
(0123)
.
The number of right cosets in [0123] =
|N|
|N
(0123)
|
=
12
1
= 12.
The orbits of N
(0123)
on {0, 1, 2, 3} are {0}, {1}, {2}, and {3}.
Nt
0
t
1
t
2
t
3
t
0
∈ [01230].
Nt
0
t
1
t
2
t
3
t
1
∈ [01231].
Nt
0
t
1
t
2
t
3
t
2
∈ [01232].
Nt
0
t
1
t
2
t
3
t
3
= Nt
0
t
1
t
2
(1 symmetric generator goes back to the double coset [012]).
• Consider N t
0
t
1
t
3
t
1
N which is denoted by [0131].
Because the relation
Nt
0
t
1
t
3
t
1
= N(13)(24)[t
0
t
1
t
2
]
(423)
= Nyxy
−1
t
2
t
1
t
3
= Nt
2
t
1
t
3
.
where Nt
2
t
1
t
3
∈ [012].
There exist {n ∈ N|N(t
0
t
1
t
2
)
n
= Nt
2
t
1
t
3
}.
Thus, N(t
0
t
1
t
2
)
(423)
= Nt
2
t
1
t
3
.
[0131] = [012]
Therefore, Nt
0
t
1
t
3
t
1
N is not a new double coset and collapses ⇒ one symmetric
genertator will take to [012].
• Consider N t
0
t
1
t
3
t
2
N which is denoted by [0132].
N
0132
= hei = N
(0132)
.
The number of right cosets in [0132] =
|N|
|N
(0132)
|
=
12
1
= 12.
The orbits of N
(0132)
on {0,1,2,3} are {0}, {1}, {2}, and {3}.
Nt
0
t
1
t
3
t
2
t
0
∈ [01320].
Nt
0
t
1
t
3
t
2
t
1
∈ [01321].
Nt
0
t
1
t
3
t
2
t
2
= Nt
0
t
1
t
3
(1 symmetric generator takes back to the double coset
[013]).
Nt
0
t
1
t
3
t
2
t
3
∈ [01323].

56
• Consider N t
0
t
1
t
3
t
0
N denoted by [0130].
N
0130
= hei. The right cosets in [0130] are not distinct. But,
t
0
t
1
t
3
t
0
= t
0
t
1
(12)(34)t
3
t
0
t
3
= (12)(34)t
3
t
2
t
3
t
0
t
3
= (12)(34)(23)(14)t
3
t
2
t
3
t
3
t
0
t
3
= (13)(24)t
3
t
2
t
0
t
3
.
Thus, 0130 ≈ 3203.
Therefore, N
(0130)
= {n ∈ N|N(0130)
n
= N(3203)}.
N(0130)
(12)(34)
= N3203 = N0130 ⇒ (12)(34) ∈ N
(0130)
N
(0130)
≥ {e, (12)(34)} = h(12)(34)i.
The number of right cosets in [0130] =
|N|
|N
(0130)
|
=
12
2
= 6.
The orbits of N
(0132)
on {0,1,2,3} are {1, 2} and {0, 3}.
Nt
0
t
1
t
3
t
0
t
1
∈ [01301] (2 symmetric generators take to the double coset [01301]).
Nt
0
t
1
t
3
t
0
t
0
= Nt
0
t
1
t
3
(2 symmetric generators go back to the double coset [013]).
We now continue the DCE by procedding in this manner until we obtain all of the 20
double cosets [w]. Now, we can determine the index of N in G.
G =
2
∗
4
:A
4
(12)(34)t
4
t
3
t
4
=t
4
t
3
|G| ≤ (|N| +
|N|
|N
(0)
|
+
|N|
|N
(01)
|
+
|N|
|N
(012)
|
+ · · · +
|N|
|N
(01231243)
|
) × |N|
|G| ≤ (1 + 4 + 12 + 12 + 12 + 12 + 6 + 12 + 6 + 12 + 12 + 12+
12 + 12 + 6 + 12 + 4 + 4 + 1 + 1) × 12
|G| ≤ (165 × 12)
|G| ≤1980

57
Figure 3.2: Cayley Diagram for L
2
(11) × 3 Over A
4
58
3.2.2 Proof of the Isomorphism
The composition series for
G =< x, y, t|x
2
, y
3
, (xy)
3
, (y
−1
x
−1
yx)
2
, t
2
, (t, y), (xt)
5
> .
is G ⊇ G
1
⊇ G
2
, where G = (G/G
1
)(G
1
/G
2
) = (G/G
1
)(G
1
/1) = L
2
(11)C
3
.
Now, we want to determine the extension type of this group.
> CompositionFactors(G1);
G
| A(1, 11) = L(2, 11)
*
| Cyclic(3)
1
Since the center of G is of order 3, we might have a central extension. Moreover, by
looking at the normal lattice of G, we see that it has a normal subgroup of order 3.
Thus, this is not a semi-direct product. Now, we want to check if it is a direct product of
L
2
(11) by C
3
. Since the minimal normal subgroups is of order equal to 660 × 3 = 1980,
it is clear that we have a direct product of L
2
(11) by C
3
.
> D:=DirectProduct(CyclicGroup(3),PSL(2,11));
> s:=IsIsomorphic(D,G1);
> s;
true
By using ATLAS, a presentation for L
2
(11) is
< a, b|a
2
, b
3
, (ab)
11
, (a, babab)
2
>
Moreover, since it is a direct product, an element of order 3 commuts with all generartors
of L
2
(11). Also, the subgroup of order 3 must be a generator of the center of G =
L
2
(11) × 3.
> HH<a,b,c>:=Group<a,b,c|aˆ2,bˆ3,(a
*
b)ˆ11,(a,b
*
a
*
b
*
a
*
b)ˆ2,
cˆ3,(a,c),(b,c)>;
> #HH;
1980
> f2,H2,k2:=CosetAction(HH,sub<HH|Id(HH)>);
> s:=IsIsomorphic(H2,G1);
> s;
true
So, we have proved that G
∼
=
L
2
(11) × 3.

59
3.3 Factor L
2
(11) × 3 by The Center of G
By looking at the Cayley diagram of G =
2
∗
4
:A
4
xt
0
t
3
t
0
=t
0
t
3
∼
=
L
2
(11) × 3 over A
4
, we
see that the center of G is hm ∗ 01231203i.
t
0
t
1
t
2
t
3
t
1
t
2
t
0
t
3
= m
−1
= xyx
= (102)
We want to factor G by the center
⇒ mt
0
t
1
t
2
t
3
t
1
t
2
t
0
t
3
= e
t
0
t
1
t
2
t
3
t
1
t
2
t
0
t
3
= m
−1
t
0
t
1
t
2
t
3
t
1
t
2
t
0
t
3
= xyx
t
0
t
1
t
2
t
3
= xyxt
3
t
0
t
2
t
1
Thus, By adding the new relation
(tt
x
y
t
x
y
y
t
x
t
x
y
t
x
y
y
tt
x
) = xyx
to the representation of G, we get
G = 2
∗
4
: A
4
= hx, y, t|x
2
, y
3
, (xy)
3
, (y
−1
x
−1
yx)
2
, t
2
, (t, y), (xt)
5
, (tt
x
y
t
x
y
y
t
x
t
x
y
t
x
y
y
tt
x
) = xyxi,
where N = A
4
= hx, yi = h(12)(30), (123)i.
Let t = t
4
→ t
0
.
Conjugate Nt
i
where i = 0, 1, 2, 3 by 01231203=xyx.
Nt
0
01231203
= t
2
Nt
1
01231203
= t
0
Nt
2
01231203
= t
1
Nt
3
01231203
= t
3
If we conjugate t
0
t
1
t
2
t
3
= (142)t
3
t
0
t
2
t
1
by all elements in A
4
, we will have the following
relations:

60
0123 ≈ 3021 ≈ 1320
3210 ≈ 0312 ≈ 2013
2301 ≈ 1203 ≈ 3102
1032 ≈ 2130 ≈ 0231
3.4 L
2
(11) as a Homomorphic Image of 2
∗
4
: A
4
3.4.1 The Construction of L
2
(11) over A
4
• Consider N eN which is denoted by [∗].
The number of right cosets in [∗] =
|N|
|N|
=
12
12
= 1.
The orbit of N on {0,1,2,3} is {0,1,2,3}.
Pick a representative from the orbit {0,1,2,3}, say 0, and determine the double
coset that contain Nt
0
.
Word of length 1.
• Consider N t
0
N which is denoted by [0].
N
0
= h(123), (132)i = N
(0)
.
The number of right cosets in [0] is equal to
|N|
|N
(0)
|
=
12
3
= 4.
The orbit of N
(0)
on {0,1,2,3} are {0} and {1,2,3}.
Nt
0
t
0
= N ∈ [∗] (1 symmetric generators goes back to the double coset [∗]).
Nt
0
t
1
∈ [01] (3 symmetric generators take to the double coset [01]).
Word of length 2.
• Consider N t
0
t
1
N which is denoted by [01].
N
01
= hei = N
(01)
.
The number of right cosets in [01] =
|N|
|N
(01)
|
=
12
1
= 12.
The orbits of N
(01)
on {0,1,2,3} are {0}, {1}, {2}, and {3}.
Nt
0
t
1
t
0
∈ [010].
Nt
0
t
1
t
1
= Nt
0
(1 symmetric generator goes back to the double coset [0]).
Nt
0
t
1
t
2
∈ [012].
Nt
0
t
1
t
3
∈ [013].
Word of length 3.

61
• Consider N t
0
t
1
t
0
N which is denoted by [010].
Because the relation
Nt
0
t
1
t
0
= N(14)(23)t
0
t
1
= Nx
y
t
0
t
1
where Nt
0
t
1
∈ [01].
There exist {n ∈ N|N(t
0
t
1
)
n
= Nt
0
t
1
}.
Thus, N(t
0
t
1
)
e
= Nt
0
t
1
. Nt
0
t
1
t
0
∈ [01].
Therefore, N t
0
t
1
t
0
N is not a new double coset and collapses ⇒ one symmetric
genertator will take to [01].
• Consider N t
0
t
1
t
2
N which is denoted by [012].
N
012
= hei = N
(012)
.
The number of right cosets in [012] is equal to
|N|
|N
(012)
|
=
12
1
= 12.
The orbits of N
(012)
on {0,1,2,3} are {0}, {1}, {2}, and {3}.
Nt
0
t
1
t
2
t
0
∈ [0120].
Nt
0
t
1
t
2
t
1
∈ [0121].
Nt
0
t
1
t
2
t
2
= Nt
0
t
1
(1 symmetric generators goes back to the double coset [01]).
Nt
0
t
1
t
2
t
3
∈ [0123].
• Consider N t
0
t
1
t
3
N which is denoted by [013].
N
013
= hei = N
(013)
.
The number of right cosets in [013] is equal to
|N|
|N
(013)
|
=
12
1
= 12.
The orbits of N
(013)
on {0,1,2,3} are {0}, {1}, {2}, and {3}.
Nt
0
t
1
t
3
t
0
∈ [0130].
Nt
0
t
1
t
3
t
1
∈ [0131].
Nt
0
t
1
t
3
t
2
∈ [0132].
Nt
0
t
1
t
3
t
3
= Nt
0
t
1
(1 symmetric generators goes back to the double coset [01]).
We keep working on the DCE by procedding in this manner until we obtain a word of
length 4. By finding out all of the 8 double cosets [w], we can determine the index of
N in G.
G =
2
∗
4
:A
4
t
0
t
1
t
2
t
3
=xyxt
3
t
0
t
2
t
1

62
|G| ≤ (|N| +
|N|
|N
(0)
|
+
|N|
|N
(01)
|
+
|N|
|N
(012)
|
+ . . . +
|N|
|N
(0132)
|
) × |N|
|G| ≤ (1 + 4 + 12 + 12 + 12 + 6 + 4 + 4) × 12
|G| ≤ (55 × 12)
|G| ≤660
Figure 3.3: Cayley Diagram for L
2
(11) Over A
4
The following computer-based proof gives that G
∼
=
L
2
(11).
> G<x,y,t>:=Group<x,y,t|xˆ2,yˆ3,(x
*
y)ˆ3,(yˆ-1
*
xˆ-1
*
y
*
x)ˆ2,\
> tˆ2,(t,y),(x
*
t)ˆ5,(t
*
(tˆx)ˆy
*
((tˆx)ˆy)ˆy
*
tˆ(x)
*
\
> (tˆx)ˆy
*
((tˆx)ˆy)ˆy
*
t
*
tˆ(x))=(x
*
y
*
x)>;
> f,G1,k:=CosetAction(G,sub<G|x,y>);
> CompositionFactors(G1);
G
| A(1, 11) = L(2, 11)
1
In the next section, we will describe how such an isomorphism can be proved by hand
(manually).
63
3.5 P GL
2
(11) as a Homorphic Image of 2
∗
5
: D
10
3.5.1 The Construction of P GL
2
(11) over D
10
Consider the group
G = 2
∗
5
: D
10
= hx, y, t|x
5
, y
2
, (xy)
2
, t
2
, (t, y), (xt)
5
, (xtt
x
)
3
i
factored by [xt]
5
.
N = D
10
= hx, yi = h(12345), (14)(23)i and let t = t
5
→ t
0
. So,
(xt)
5
= e
(xt
0
)
5
= e
x
5
t
0
x
4
t
0
x
3
t
0
x
2
t
0
x
t
0
= e
t
4
t
3
t
2
t
1
t
0
= e
t
4
t
3
t
2
= t
0
t
1
t
4
t
3
t
2
= t
0
t
1
⇒ Nt
4
t
3
t
2
= Nt
0
t
1
(xtt
x
)
3
= e
(xt
0
t
1
)
3
= e
x
3
t
0
t
1
x
2
t
0
t
1
x
t
0
t
1
= e
(14203)t
2
t
3
t
1
t
2
t
0
t
1
= e
(14203)t
2
t
3
t
1
= t
1
t
0
t
2
⇒ Nt
2
t
3
t
1
= Nt
1
t
0
t
2
If we conjugate the previous relation (N t
4
t
3
t
2
= Nt
0
t
1
) by all elements in D
10
, we will
have the following relations:
Nt
4
t
3
t
2
= Nt
0
t
1
, Nt
1
t
2
t
3
= Nt
0
t
4
,
Nt
0
t
1
t
2
= Nt
4
t
3
, Nt
2
t
3
t
4
= Nt
1
t
0
,
Nt
2
t
1
t
0
= Nt
3
t
4
, Nt
3
t
4
t
0
= Nt
2
t
1
,
Nt
4
t
0
t
1
= Nt
3
t
2
, Nt
0
t
4
t
3
= Nt
1
t
2
,
Nt
3
t
2
t
1
= Nt
4
t
0
, Nt
1
t
0
t
4
= Nt
2
t
3
.
If we conjugate the previous relation (N t
2
t
3
t
1
= N t
1
t
0
t
2
) by all elements in D
10
, we
will have the following relations:

64
Nt
2
t
3
t
1
= Nt
1
t
0
t
2
, Nt
3
t
2
t
4
= Nt
4
t
0
t
3
,
Nt
2
t
1
t
3
= Nt
3
t
4
t
2
, Nt
4
t
3
t
0
= Nt
5
t
1
t
4
,
Nt
0
t
4
t
1
= Nt
1
t
2
t
0
, Nt
1
t
0
t
2
= Nt
2
t
3
t
1
,
Nt
3
t
4
t
2
= Nt
2
t
1
t
3
, Nt
1
t
2
t
0
= Nt
0
t
4
t
1
,
Nt
4
t
0
t
3
= Nt
3
t
2
t
4
, Nt
0
t
1
t
4
= Nt
4
t
3
t
0
.
The double coset enumeration:
• Consider N eN which is denoted by [∗].
The number of right cosets in [∗] is equal to
|N|
|N|
=
10
10
= 1.
The orbit of N on {0,1,2,3,4} is {0,1,2,3,4}.
Pick a representative from the orbit {0,1,2,3,4}, say 0, and determine the double
coset that contain Nt
0
.
Word of length 1.
• Consider N t
0
N which is denoted by [0].
N
0
= h(14)(23)i = N
(0)
.
The number of right cosets in [0] =
|N|
|N
(0)
|
=
10
2
= 5.
The orbit of N
(0)
on{0,1,2,3,4} are {0}, {1,4} and {2,3}.
Nt
0
t
0
∈ [∗] (1 symmetric generator goes back to the double coset [∗]).
Nt
0
t
1
∈ [01].
Nt
0
t
2
∈ [02].
Word of length 2.
• Consider N t
0
t
1
N which is denoted by [01].
N
01
= hei = N
(01)
.
The number of right cosets in [01] is equal to
|N|
|N
(01)
|
=
10
1
= 10.
The orbits of N
(01)
on {0,1,2,3,4} are {0}, {1}, {2}, {3} and {4}.
Nt
0
t
1
t
0
∈ [010].
Nt
0
t
1
t
1
= Nt
0
(1 symmetric generator goes back to the double coset [0]).
Nt
0
t
1
t
2
∈ [012].
Nt
0
t
1
t
3
∈ [013].
Nt
0
t
1
t
4
∈ [014].

65
• Consider N t
0
t
2
N which is denoted by [01].
N
02
= hei = N
(02)
.
The number of right cosets in [02] =
|N|
|N
(02)
|
=
10
1
= 10.
The orbits of N
(02)
on {0,1,2,3,4} are {0}, {1}, {2}, {3} and {4}.
Nt
0
t
2
t
0
∈ [020].
Nt
0
t
2
t
1
∈ [021].
Nt
0
t
2
t
2
= Nt
0
(1 symmetric generator goes back to the double coset [0]).
Nt
0
t
2
t
3
∈ [023].
Nt
0
t
2
t
4
∈ [024].
Word of length 3.
• Consider N t
0
t
1
t
2
N which is denoted by [012].
Because the relation
Nt
0
t
1
t
2
= N(t
0
t
1
)
(13)(40)
= Nt
4
t
3
where Nt
4
t
3
∈ [01].
There exist {n ∈ N|N(t
0
t
1
t
2
)
n
= Nt
4
t
3
}.
Thus, N(t
0
t
1
t
2
)
(13)(40)
= Nt
4
t
3
.
[012] = [01]
Therefore, N t
0
t
1
t
2
N is not a new double coset and collapses ⇒ one symmetric
genertator will take to the double coset [01].
• Consider N t
0
t
1
t
3
N which is denoted by [013].
N
013
= hei = N
(013)
.
The number of right cosets in [013] =
|N|
|N
(013)
|
=
10
1
= 10.
The orbits of N
(013)
on {0,1,2,3,4} are {0}, {1}, {2}, {3} and {4}.
Nt
0
t
1
t
3
t
0
∈ [0130].
Nt
0
t
1
t
3
t
1
∈ [0131].
Nt
0
t
1
t
3
t
2
∈ [0132].
Nt
0
t
1
t
3
t
3
= Nt
0
t
1
(1 symmetric generator goes back to the double coset [01]).
Nt
0
t
1
t
3
t
4
∈ [0134].

66
• Consider N t
0
t
1
t
4
N which is denoted by [014].
N
014
= hei. The right cosets in [014] are not distinct. From previous relations,
we have that
014 ≈ 430
Therefore, N
(014)
= {n ∈ N|N(014)
n
= N(430)}.
N(014)
(13)(45)
= N430 = N014 ⇒ (13)(45) ∈ N
(014)
N
(014)
≥ {e, (13)(45)} = h(13)(45)i.
The number of right cosets in [014] =
|N|
|N
(014)
|
=
10
2
= 5.
The orbits of N
(014)
on {0,1,2,3,4} are {2}, {1,3}, and {0,4}. Nt
0
t
1
t
4
t
2
∈ [0142].
Nt
0
t
1
t
4
t
1
∈ [0141].
Nt
0
t
1
t
4
t
4
= Nt
0
t
1
(1 symmetric generator goes back to the double coset [01]).
• Consider N t
0
t
1
t
0
N which is denoted by [010].
N
010
= hei = N
(010)
.
The number of right cosets in [010] =
|N|
|N
(010)
|
=
10
1
= 10.
The orbits of N
(010)
on {0,1,2,3,4} are {0}, {1}, {2}, {3} and {4}.
Nt
0
t
1
t
0
t
0
= Nt
0
t
1
(1 symmetric generator takes back to the double coset [01]).
Nt
0
t
1
t
0
t
1
∈ [0101].
Nt
0
t
1
t
0
t
2
∈ [0102].
Nt
0
t
1
t
0
t
3
∈ [0103].
Nt
0
t
1
t
0
t
4
∈ [0104].
.
.
.
By continuing this process, we find out the all 19 double cosets [w]. Now, we can
determine the index of N in G.
G =
2
∗
4
:A
4
(12)(34)t
4
t
3
t
4
=t
4
t
3
|G| ≤
|N| +
|N|
|N
(0)
|
+
|N|
|N
(01)
|
+
|N|
|N
(02)
|
+ . . . +
|N|
|N
(01310)
|
+
|N|
|N
(01010)
|
× |N |

67
|G| ≤ (1 + 5 + 10 + 10 + 10 + 5 + 10 + 5 + 10+
10 + 10 + 5 + 5 + 10 + 5 + 10 + 5 + 1 + 5) × 10
|G| ≤ (132 × 10)
|G| ≤1320
Figure 3.4: Cayley Diagram for P GL
2
(11) Over D
10
3.5.2 Proof of the Isomorphism
Now, we want to show that G is isomorphic to P GL
2
(11). First, we will
construct L
2
(11), then P GL
2
(11). After this, we see that G is isomorphic to P GL
2
(11)
by constructing a homomorphism φ from the progenitor 2
∗
5
: D
10
onto P GL
2
(11). Now,
we want to write a permutation for L
2
(11) such that L
2
(11) = hα, β, γi, where
α : x 7−→ x + 1.
β : x 7−→ kx.
γ : x 7−→ −
1
x
.
’k’ is a non-zero square whose powers give all non-zero squares in
Z
11
= {0, 2, 3, 4, 5, 6, 7, 8, 9, 10}.

68
Note 3.2. We will replace 11 by 0.
Table 3.2: Z
11
Squares
0
2
1
2
2
2
3
2
4
2
5
2
6
2
7
2
8
2
9
2
10
2
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
0 1 4 9 5 3 3 5 9 4 1
Thus, the nonzero squares in Z
11
is {1,3,4,5,9}. By using MAGMA, we can
see what gives the power of the squares.
> Q:={}; for i in [1..10] do Q:=Q join {iˆ2 mod 11}; end for;
> Q;
{1, 3, 4, 5, 9}
> T:={}; for i in Q do T:=T join {iˆ2 mod 11};
> if T eq Q then i; end if; end for;
9
We find that k = 9. Now, we want to write down the permutation for α, β, and γ. To
know the inverse of i ∀1 ≤ i ≤ 10, we run the following code
F:=GaloisField(11);
F!1ˆ-1; F!2ˆ-1; F!3ˆ-1; F!4ˆ-1; F!5ˆ-1;
F!6ˆ-1; F!7ˆ-1; F!8ˆ-1; F!9ˆ-1; F!10ˆ-1;
Table 3.3: Permutation of α : x 7−→ x + 1
0 1 2 3 4 5 6 7 8 9 10
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
1 2 3 4 5 6 7 8 9 10 0
Table 3.4: Permutation of β : x 7−→ 9x
0 1 2 3 4 5 6 7 8 9 10
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
0 9 7 5 3 1 10 8 6 4 2
We use MAGMA to confirm that hα, β, γi = L
2
(11).
α = (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 0)(∞).
β = (1, 9, 4, 3, 5)(2, 7, 8, 6, 10).
γ = (0, ∞)(1, 10)(2, 5)(3, 7)(4, 8)(6, 9).

69
Table 3.5: Permutation of γ : x 7−→ −1/x = −x
−1
0 1 2 3 4 5 6 7 8 9 10
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
∞ 10 5 7 8 2 9 3 4 6 1
S:=Sym(12);
alpha:=S!(1,2,3,4,5,6,7,8,9,10,11);
beta:=S!(1,9,4,3,5)(2,7,8,6,10);
gamma:=S!(12,11)(1,10)(2,5)(3,7)(4,8)(6,9);
N:=sub<S|alpha,beta,gamma>;
> s,u:=IsIsomorphic(PSL(2,11),N);
> s;
true
Since it says true, the representation of the Linear Fractional maps LF
2
(11) = L
2
(11)
is given by
hα, β, γ|α
11
, β
5
, γ
2
, α
β
α
−9
, (βγ)
2
, (αγ)
3
i.
Now, we want to write the permutation representation for P GL(2, 11) by adding δ :
x 7−→ −x and find its action on α, β, and γ.
Note 3.3. We denote δ by aut in MAGMA.
Table 3.6: Permutation of δ : x 7−→ −x
0 1 2 3 4 5 6 7 8 9 10
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
0 10 9 8 7 6 5 4 3 2 1
The MAGMA input for P GL(2, 11) is as the following:
aut:=S!(1,10)(2,9)(3,8)(4,7)(5,6);
pgl211:=sub<S|N,aut>;
#pgl211;
s1,u1:=IsIsomorphic(PGL(2,11),pgl211);
> s1;
true
s2,u2:=IsIsomorphic(G1,pgl211);
> s2;
true

70
alphaˆaut;
betaˆaut;
gamaˆaut;
Thus, the representation of P GL(2, 11) is given by
hα, β, γ, δ|α
11
, β
5
, γ
2
, α
β
α
−9
, (βγ)
2
, (αγ)
3
, δ
2
, α
δ
= α
−1
, β
δ
= β, γ
δ
= γi.
u2;
xx:=pgl211!(1,5,8,11,4)(6,7,12,9,10);
yy:=pgl211!(1,5)(2,3)(4,8)(6,7)(10,12);
tinf:=pgl211!(1,4)(2,6)(3,7)(5,8)(9,11)(10,12);
We define a homomorphism φ from the progenitor 2
∗
5
: D
10
to P GL
2
(11) by
φ(x) = (1, 5, 8, 0, 4)(6, 7, ∞, 9, 10).
φ(y) = (1, 5)(2, 3)(4, 8)(6, 7)(10, ∞).
φ(t
∞
) = (1, 4)(2, 6)(3, 7)(5, 8)(9, 0)(10, ∞).
φ(G)
∼
=
P GL(2, 11)
To show that, I have to find a linear fractional maps in P GL(2, 11) for φ(x), φ(y), and
φ(t) such that x 7−→
ax+b
cx+d
, ad − bc 6= 0 for x to be in P GL(2, 11).
• Map for φ(x).
Since φ(x) = (1, 5, 8, 0, 4)(6, 7, ∞, 9, 10), we have
0 7−→
b
d
= 4 ⇒ b = 4d.
8 7−→
8a+b
8c+d
= 0 ⇒ 8a + b = 0 ⇒ b = −8a ≡
11
3a.
∞ 7−→
a
c
= 9 ⇒ a = 9c ⇒ c = 9
−1
a = 5a.
So, let a = 1. We have b = 3, d = 4
−1
b = 3(4
−1
) = 3(3) = 9, and c = 5.
Moreover, since ad − bc = (1)(9) − (3)(5) = 9 − 15 6= 0, our map is in P GL(2, 11).
The map η is
η 7−→
η+3
5η+9
.
• Map for φ(y).
Since φ(x) = (1, 5)(2, 3)(4, 8)(6, 7)(10, ∞), we have
1 7−→
a+b
c+d
= 5 ⇒ a + b = 5c + 5d.

71
10 7−→
10a+b
10c+d
= ∞ ⇒ 10c + d = 0 ⇒ d = −10c ≡
11
c.
∞ 7−→
a
c
= 10 ⇒ a = 10c.
So, let c = 1. We have a = 10, d = 1, and a+b = 5c+5d ⇒ 10+b = 5+5 ⇒ b = 0.
Moreover, since ad − bc = (10)(1) − (0)(1) = 10 6= 0, our map is in PGL(2, 11).
The map η is
η 7−→
10η
η+1
.
• Map for φ(t).
Since φ(x) = (1, 4)(2, 6)(3, 7)(5, 8)(9, 0)(10, ∞), we have
1 7−→
a+b
c+d
= 4 ⇒ a + b = 4c + 4d.
9 7−→
9a+b
9c+d
= 0 ⇒ 9a + b = 0 ⇒ b = −9a ≡
11
5a.
0 7−→
b
d
= 9 ⇒ b = 9d.
So, let d = 1. We have b = 9, d = 1, a = 5
−1
b = 9(9) = 81 ≡
11
4, and
4 + 9 = 4c + 4 ⇒ c = 9(4
−1
) = 27 ≡
11
5.
Moreover, since ad − bc = (4)(9) − (9)(5) = 2 6= 0 and it is not a square, our map
is in P GL(2, 11). The map η is
η 7−→
4η+9
5η+9
.
We construct a homomorphism φ from the progenitor 2
∗
5
: D
10
to P GL
2
(11) by defining
φ(x) =
η + 3
5η + 9
= (1, 5, 8, 0, 4)(6, 7, ∞, 9, 10).
φ(y) =
10η
η + 1
= (1, 5)(2, 3)(4, 8)(6, 7)(10, ∞).
Since the orders of φ(x),φ(y), and φ(x)φ(y) are 5, 2, and 2, respectively,
N =< φ(x), φ(y) >
∼
=
D
10
.
Now, let
φ(t
∞
) =
4η + 9
5η + 9
= (1, 4)(2, 6)(3, 7)(5, 8)(9, 0)(10, ∞).
It is readily verified that P GL
2
(11)
∼
=
< φ(x), φ(y), φ(t
∞
) >. Next, we show that φ
preserve the operation of 2
∗
5
: D
10
. We find that
φ(t
∞
)
N
= 5 and that N permutes

72
the five images of t
∞
, by conjugation, as the group D
10
. Thus,
φ(t
1
) = φ(t
x
∞
) = (1, 5)(2, 7)(3, ∞)(4, 10)(6, 9)(8, 0),
φ(t
2
) = φ(t
x
1
) = (1, 6)(2, ∞)(3, 9)(4, 0)(5, 8)(7, 10),
φ(t
3
) = φ(t
x
2
) = (1, 4)(2, 9)(3, 10)(5, 7)(6, ∞)(8, 0),
φ(t
0
) = φ(t
x
3
) = (1, 5)(2, 10)(3, 6)(4, 0)(7, 9)(8, ∞),
φ(t
∞
) = (1, 4)(2, 6)(3, 7)(5, 8)(9, 0)(10, ∞).
Thus, N permutes the five images of t
∞
, by conjugation, as the group D
10
given by:
φ(x) : (φ(t
1
), φ(t
2
), φ(t
3
), φ(t
0
), φ(t
∞
)),
φ(y) : (φ(t
1
), φ(t
0
))(φ(t
2
), φ(t
3
)).
Hence,
φ
2
∗
5
: D
10
= P GL
2
(11).
Look at the additional relation given by [xt
∞
]
5
= e ⇔ t
0
t
3
t
2
t
1
t
∞
= e
is satisfied in P GL
2
(11), because φ(t
0
)φ(t
3
)φ(t
2
)φ(t
1
)φ(t
∞
) = e
acts as identity on (φ(t
1
))(φ(t
2
))(φ(t
3
))(φ(t
0
))(φ(t
∞
)) = e,
by conjugation, on the images of the five symmetric generators.
This shows that P GL
2
(11) is an image of G.
Thus, |G| ≥ |P GL
2
(11)|; but |G| ≤ 1320 = |P GL
2
(11)|,
and so the equality holds and G
∼
=
P GL
2
(11).
G =
2
∗
5
:D
10
t
0
t
3
t
2
t
1
t
∞
=1
∼
=
P GL
2
(11).
To have more homomorphic images, we factored the pogenitor 2
∗
5
: D
10
by the following
relators
(xt)
a
, (xyt
x
2
)
b
, (xtt
x
)
c
, (ytt
x
2
t
x
)
d
73
Table 3.7: Some finite images of the Progenitor 2
∗
5
: D
10
a b c d Index of N in G Order of G Shape of G
5 0 2 3 6 60 A
5
0 2 2 3 12 120 A
5
× 2
0 2 2 6 24 240 2
2
× A
5
0 2 3 2 48 480 4 • (2 × A
5
)
8 2 5 3 72 720 A
6
: 2
∼
=
P GL
2
(9)
5 2 3 0 132 1320 P GL
2
(11)
4 2 4 0 144 1440 P GL
2
(9) × 2
8 2 0 3 216 2160 (3 : A
6
) : 2
4 2 0 6 264 2640 P GL
2
(11) × 2
5 2 9 5 342 3420 L
2
(19)
0 2 3 3 684 6840 P GL
2
(19)
5 2 6 6 972 9720 3
4
• (2 × A
5
)
4 2 0 7 2436 24360 P GL
2
(29)
0 2 4 3 4320 43200 P GL
2
(9) × A
5
10 2 0 3 12960 129600 (A
5
× 3) • P GL
2
(9)
9 2 3 0 41040 410400 (A
5
× L
2
(19)) : 2
6 2 3 10 75000 750000 (2 × 5
5
) • (2 × A
5
)
74
Chapter 4
Methods for Obtaining
Homomorphic Images
In this chapter, we will introduce some useful techniques to find some finite
images of an involutory progenitors m
∗
n
: N, where m = 2, 3, . . . and the non-involutory
(monomial) progenitors p
∗
n
:
m
N, where p = 3, 5, 7, . . ..
• Factoring m
∗
n
: N and p
∗
n
:
m
N by all first order relations.
All relations of the first order that the progenitor can be factored by are obtained
by computing the conjugacy classes of N. Thus, we will obtain a list of repre-
sentitive of classes. Then, we compute the centralisers of representitives of each
non-identity class and determine its orbits.
Example 4.1. Consider the progenitor of 2
∗
3
: S
3
that has the following presen-
tation
< x, y|x
3
, y
2
, (xy)
2
>
To find all of the first order relations for the progenitor 2
∗
3
: S
3
, we run the
following code. Then, we summarize the result in the table 4.1.
C:=Classes(N); c;
C2:=Centraliser(N,N!(1,2)); C2;
Orbits(C2);
C3:=Centraliser(N,N!(1,2,3)); C3;
Orbits(C3);

75
Table 4.1: Conjugacy Classes of S
3
Class Representitive of the class # of elements in the class Orbits
C
1
identity 1 {1},{2},{3}
C
2
y = (1, 2) 3 {1,2},{3}
C
3
x = (1, 2, 3) 2 {1,2,3}
Now, we pick a representitive from each orbit for the non-identity class C
2
and
C
3
. Thus, the all possible relations are
(yt)
a
, (yt
x
2
)
b
, and (xt)
c
, where t ∼ t
1
and t
x
2
= t
3
.
Hence, for finite images, we factor 2
∗
3
: S
3
by the relations
(yt)
a
, (yt
x
2
)
b
, and (xt)
c
Hence, the following homomorphic images were obtained.
Table 4.2: Some finite images of the Progenitor 2
∗
3
: S
3
a b c Index in G Order of G Shape of G
0 2 2 2 12 (2 × 3) : 2
0 2 3 4 24 S
4
0 2 4 8 48 2
3
: S
3
0 2 5 20 120 2 × A
5
• Factoring 2
∗
n
: N by relations found by Lemma.
Lemma 4.2 (Curtis). N ∩ ht
i
, t
j
i ≤ C
N
(N
ij
), where N
ij
denotes the stabilizer
in N of the two points i and j.
To apply this method, we find stabiliser of two elements and determining the cen-
traliser of those points. Moreover, the lemma deals with two types of permutations
1. Permutation π that fixes t
i
and t
j
.
The relation of this type have the following form (t
i
t
j
)
k
= π, where k is even.
2. Permutation π that sends t
i
to t
j
and vice versa.
The relation of this type have the following form (πt)
k
= 1, where π ∈ N
and k is odd.
76
Example 4.3. Consider the progenitor of 2
∗
4
: S
4
that has the following presen-
tation
< x, y|x
4
, y
2
, (xy)
3
>
To make this progenitor finite, we have to factore it by relations that satisfy the
lemma. First, we have to insert a new variable t ≈ t
1
and find all elements that
centralise the subgroup < t
1
>. So, the point stabiliser of t
1
is
N
1
= {(2, 3), (3, 4)} = {y
x
, x
2
yx
2
}
Then, the presentation for P = 2
∗
4
: S
4
becomes as follow:
< x, y, t|x
4
, y
2
, (xy)
3
, t
2
, (t, y
x
), (t, x
2
yx
2
) >
Now, we have to apply the lemma by finding the centraliser of two point stabiliser
N
t
1
t
4
such that
N ∩ ht
1
, t
4
i ≤ C
N
(N
14
)
≤ C
N
((2, 3))
We want to find n ∈ N such that (2, 3)
n
= (2, 3). Hence, the centralisers of N
14
are the following permutations
(1, 4) = y
x
and (2, 3) = x
2
yx
2
.
We noticed that (1,4) is a permutation that sends 1 to 4 and 4 to 1 and (2,3) is
a permutation that fixes 1 and 4. So, we might choose either one to factore the
progenitor by. The form for these relations is given as bellow
(2, 3) → (t
1
t
4
)
k
= (2, 3) ⇒ (tt
x
3
)
k
= x
2
yx
2
, where k is even.
(1, 4) → ((1, 4)t
1
)
k
= 1 ⇒ (y
x
t)
k
= 1, where k is odd.
The presentation for the progenitor over S
4
is
< x, y, t|x
4
, y
2
, (xy)
3
, t
2
, (t, y
x
), (t, x
2
yx
2
), (tt
x
3
)
k
= x
2
yx
2
, (y
x
t)
l
= 1 > .
The following homomorphic image were obtained.

77
2
∗
4
:S
4
[tt
x
]
2
=x
2
yx
2
∼
=
P GL
2
(7).
• Factoring m
∗
n
: N and p
∗
n
:
m
N by (t
i
, t
j
).
Theorem 4.4. The progenitor G = m
∗
n
: N, where m
∗
n
=< t
1
> ∗ . . . ∗ < t
n
>
and |t
i
| = m, 1 ≤ i ≤ n and N ≤ U(m) o S
n
, where U(m) is the group of
positive integers less than m and relative prime to m under multiplicaion modulo
m, factored by the relations (t
i
, t
j
), i, j ∈ {1, 2, . . . , n} is isomorphic to m
n
: N.
m
∗
n
: N
(t
i
, t
j
), i, j ∈ {1, 2, . . . , n}
∼
=
m
n
: N.
Example 4.5. Let G = 3
∗
3
: S
3
, where S
3
is generated by
< x, y >=< (123), (12) >.
The presentation for this progenitor is
< x, y, t|x
3
, y
2
, (xy)
2
, t
3
>
This progenitor is infinite and in order to make it finite, we have to factore it by
relations. Moreover, to prove it is isomorphic to 3
2
: S
3
, we have to find (t
i
, t
j
),
where i, j ∈ {1, 2, 3}. Thus, we want first to find a permutation in S
3
that fix
t = t
1
, and we find it is < (2, 3) = xy >= N
1
. Then, we have to find the orbits of
N
1
on {0,1,2} which are {0,2} and {1}. We pick a representitive from {0,2}, say
2. Thus, we obtain the desired relation (t
1
, t
2
) = (t, t
x
). By adding this relator
to our progenitor, the homomorphic image is 3
3
: S
3
. By using MAGMA we were
able to prove the isomorphic image.
S:=Sym(3);
xx:=S!(1,2,3);
yy:=S!(1,2);
N:=sub<S|xx,yy>;
G<x,y,t>:=Group<x,y,t|xˆ3,yˆ2,(x
*
y)ˆ2,tˆ3,(t,x
*
y),(t,tˆx)>;
f,G1,k:=CosetAction(G,sub<G|x,y>);
> CompositionFactors(G1);
G
| Cyclic(3)
*
78
| Cyclic(2)
*
| Cyclic(3)
*
| Cyclic(3)
*
| Cyclic(3)
1
By looking at the normal lattice of G, we find that there is an abelian group [4]
of order 27 = 3
3
. The symmetric presentation for [4] is
< a, b, c|a
3
, b
3
, c
3
, (a, b), (a, c), (b, c) >.
Now, we want to factor G by [4] to find q.
q,ff:=quo<G1|NL[4]>;
q;
> s:=IsIsomorphic(q,Sym(3));s;
true
We obtain that q
∼
=
S
3
generated by < q.1, q.2 >=< (123), (23) >. Now, we want
to find the action of q generators on [4] generators after store them. Thus, we
have to find the transversal of G/[4]
∼
=
q.
T:=Transversal(G1,NL[4]);
> ff(T[2]) eq q.1; ff(T[3]) eq q.2;
true true
x:=G1!(2,4,5)(3,6,7)(8,16,10)...(21,22,24)(23,26,25);
y:=G1!(2,4)(3,6)(9,12)...(15,19)(21,22)(25,26);
A:=NL[4].1;
a:=G1!(1,3,2)(4,9,8)...(18,25,24)(19,27,26);
B:=NL[4].2;
b:=G1!(1,12,9)(2,13,4)...(14,27,18)(15,19,24);
C:=NL[4].3;
c:=G1!(1,20,27)(2,21,19)...(9,17,14)(11,18,12);
The following loops are for finding the action of q elements on [4] elements. So,
we want to writ the relations between of them in terms of [4] generators.

79
for i,j,l in [1..3] do if aˆx eq aˆi
*
bˆj
*
cˆl then i,j,l;
end if; end for;
for i,j,l in [1..3] do if aˆy eq aˆi
*
bˆj
*
cˆl then i,j,l;
end if; end for;
Similarly, for b and c. The symmetric presentaion for H = [4] : q is
< a, b, c, x, y|a
3
, b
3
, c
3
, (a, b), (a, c), (b, c), x
3
, y
2
, (xy)
2
, a
x
= ab, a
y
= ab,
b
x
= bc
2
, b
y
= b
2
, c
x
= c, c
y
= c >
The following computer-based proof gives that G =
3
∗
3
:S
3
(t
1
,t
2
)
∼
=
3
3
: S
3
> f2,H2,k2:=CosetAction(H,sub<H|Id(H)>);
> s:=IsIsomorphic(H2,G1);s;
true
80
Chapter 5
Transitive Group
The objective of this chapter is to factor the progenitor m
∗
n
: N which is
infinite group by suitable relations of the form πω(t
1
, . . . , t
n
), where π ∈ N and ω is a
word in the symmetric generators, in order to find finite homomorphic images of the
infinte progenitor m
∗
n
: N. The notation m
∗
n
denots a free product of n the number of
t
i
0
s of order m, and N is a transitive subgroup of the symmetric group S
n
.
5.1 Transitive group on 8 letters
Consider the progenitor P = 2
∗
8
: N. Since there are 50 transitive group on 8
letters, define N as the 27
th
transitive subgroup on 8 letters of the symmetric group S
8
and define D to be the small group database in order to find a presentation for N.
The input code onto MAGMA is as follow:
NumberOfTransitiveGroups(8);
N:=TransitiveGroup(8,27);
D:=SmallGroupDatabase();
G:=SmallGroup(D,64,32);
f,G1,k:=CosetAction(G,sub<G|Id(G)>);
SL:=Subgroups(G1);
SL will find all subgroups H of G.
T:= {X‘subgroup: X in SL};
#T;
#T will show that there are 47 subgroups H in G.
81
TrivCore:={H:H in T| #Core(G1,H) eq 1};
#TrivCore;
#TrivCore will show that there are 21 faithful permutations representation of G.
mdeg:=Min({Index(G1,H):H in TrivCore});
mdeg gives the smallest number of letters in a permutation representation of G.
Good:={H: H in TrivCore| Index(G1,H) eq mdeg};
#Good;
#Good will show that there are 4 subgroups that give the best, in terms of the smallest
number of letters. By running this loop FPGroup(G), we obtain a presentation for
G on 8 letters with 6 generators that is isomorphic to our transitive subgroup N in the
progenitor 2
∗
8
: N.
G =<a, b, c, d, e, r|a
2
= d, b
2
, c
2
, d
2
, e
2
, r
2
, b
a
= bc, c
a
= ce, c
b
= c, d
a
= d, d
b
= de,
d
c
= dr, e
a
= er, e
b
= e, e
c
= e, e
d
= e, r
a
= r, r
b
= r, r
c
= r, r
d
= r, r
e
= r > .
Thus, we will label its generators in MAGMA as A, B, C, D, E, and R.
A:=G1!(1, 2)(3, 7)(4, 5, 8, 6);
B:=G1!(1, 3)(2, 5)(4, 8)(6, 7);
C:=G1!(1, 4)(2, 6)(3, 8)(5, 7);
D:=G1!(4, 8)(5, 6);
E:=G1!(2, 7)(5, 6);
R:=G1!(1, 3)(2, 7)(4, 8)(5, 6);
N:=sub<G1|A,B,C,D,E,R>;
Now, to search for relations, we must introduce a new variable t of order 2, let t = t
8
→ t
0
and find the stabiliser of 8, and we must write all the elements of the stabiliser in terms
of a,b,c,d,e, and r by using the Schreier system.
(2, 7)(5, 6) = e.
(2, 5)(6, 7) = ber.
(1, 3)(2, 5, 7, 6) = db.
Then, since t commutes with each generator of the one point stabiliser N
0
, we insert t
and the generators of the centraliser of < t > into our progenitor. Then the presentation
82
for P = 2
∗
8
: N becomes as follow:
< a, b, c, d, e, r, t|a
2
= d, b
2
, c
2
, d
2
, e
2
, r
2
, b
a
= bc, c
a
= ce, c
b
= c, d
a
= d, d
b
= de,
d
c
= dr, e
a
= er, e
b
= e, e
c
= e, e
d
= e, r
a
= r, r
b
= r, r
c
= r, r
d
= r, r
e
= r, t
2
, (t, e),
(t, ber), (t, db) >
Now, we will utilize the lemma by taking the stabiliser of two elements N
01
and de-
termining the centraliser of those points. The lemma deals with elements that have a
transposition (0,1), or do have either 1 or 0, or do not have either of them.
N ∩ ht
0
, t
1
i ≤ C
N
(N
01
).
N
(01)
= h(2, 7)(5, 6), (2, 5)(6, 7)i.
C
N
(N
01
) = h(1, 4)(3, 8), (1, 3)(4, 8), (2, 7)(5, 6), (2, 5)(6, 7)i.
By running the Set(C), we find that there are four elements that have a transposition
(0,1) together and by itself such as:
(1, 0)(2, 6)(3, 4)(5, 7) = aca
−1
,
(1, 0)(2, 5)(3, 4)(6, 7) = cr,
(1, 0)(2, 7)(3, 4)(5, 6) = bc,
(1, 0)(3, 4) = bce.
Thus, we have to apply the lemma as the following:
(aca
−1
t)
k
= 1,
(crt)
k
= 1,
(bcet)
k
= 1,
(bct)
k
= 1.
where k is odd.
By choosing one from the above list of relations, the presentation for this progenitor is
< a, b, c, d, e, r, t|a
2
= d, b
2
, c
2
, d
2
, e
2
, r
2
, b
a
= bc, c
a
= ce, c
b
= c, d
a
= d, d
b
= de, d
c
= dr,
e
a
= er, e
b
= e, e
c
= e, e
d
= e, r
a
= r, r
b
= r, r
c
= r, r
d
= r, r
e
= r, t
2
, (t, e), (t, ber),
(t, db), (bcet)
k
>

83
To find some finite images of the progenitor 2
∗
8
: N , we add more relations and run
them in MAGMA to find some interesting images.
< a, b, c, d, e, r, t|a
2
= d, b
2
, c
2
, d
2
, e
2
, r
2
, b
a
= bc, c
a
= ce, c
b
= c,
d
a
= d, d
b
= de, d
c
= dr, e
a
= er, e
b
= e, e
c
= e, e
d
= e, r
a
= r, r
b
= r,
r
c
= r, r
d
= r, r
e
= r, t
2
, (t, e), (t, ber), (t, db), (bcet)
k
, (dbt
c
)
l
,
(ert)
m
, (a(t
r
)
c
)
n
, (ct
b
)
o
> .
Table 5.1: Some finite images of the progenitors 2
∗
8
: N
k l m n o Index in G Order of G Shape of G
0 2 2 5 3 15 120 A
5
: 2 ≈ S
5
0 2 2 5 5 165 1320 P GL(2, 11)
5 2 2 5 0 90 720 A
6
: 2
∼
=
P GL
2
(9)
0 0 3 4 8 28224 1806336 (4 × 2) • [(L
2
(7) × L
2
(7)) : (2
2
: 2)]
5 0 3 4 0 225 14400 (A
5
× A
5
) : 4
5.1.1 Proof of The Isomorphism for The Shape of N
Consider the progenitor 2
∗
8
: N, Where N is given by
S:=Sym(8);
aa:=S!(1, 2)(3, 7)(4, 5, 8, 6);
bb:=S!(1, 3)(2, 5)(4, 8)(6, 7);
cc:=S!(1, 4)(2, 6)(3, 8)(5, 7);
dd:=S!(4, 8)(5, 6);
ee:=S!(2, 7)(5, 6);
rr:=S!(1, 3)(2, 7)(4, 8)(5, 6);
N:=sub<S|aa,bb,cc,dd,ee,rr>;
We prove below that N is isomorphic to a mixed extension of the abelian group Z
4
× Z
2
by the Dihedral group D
4
of order 8. Let’s call N = G. The transitive group G has the
following composition series
G = G ⊇ G
1
⊇ G
2
⊇ G
3
⊇ G
4
⊇ G
5
⊇ 1,
where
G = (G/G
1
)(G
1
/G
2
)(G
2
/G
3
)(G
3
/G
4
)(G
4
/G
5
)(G
5
/1) = C
2
C
2
C
2
C
2
C
2
C
2
.
84
This group has the following normal lattice
> NL:=NormalLattice(N); NL;
Normal subgroup lattice
-----------------------
[13] Order 64 Length 1 Maximal Subgroups: 10 11 12
---
[12] Order 32 Length 1 Maximal Subgroups: 7
[11] Order 32 Length 1 Maximal Subgroups: 7
[10] Order 32 Length 1 Maximal Subgroups: 7 8 9
---
[ 9] Order 16 Length 1 Maximal Subgroups: 6
[ 8] Order 16 Length 1 Maximal Subgroups: 6
[ 7] Order 16 Length 1 Maximal Subgroups: 4 5 6
---
[ 6] Order 8 Length 1 Maximal Subgroups: 3
[ 5] Order 8 Length 1 Maximal Subgroups: 3
[ 4] Order 8 Length 1 Maximal Subgroups: 3
---
[ 3] Order 4 Length 1 Maximal Subgroups: 2
---
[ 2] Order 2 Length 1 Maximal Subgroups: 1
---
[ 1] Order 1 Length 1 Maximal Subgroups:
By looking at the center of G, we see that we may have a centeral extension. Let’s check
if [4] is an abelian group or not.
> IsAbelian(NL[4]);
true
> X1:=AbelianGroup(GrpPerm,[4,2]);
> IsIsomorphic(X1,NL[4]);
true
We confirm that G
3
= 4 × 2 is the isomorphism type of [4]. Since [4]=Z
4
× Z
2
is an
abelian subgroup of G, we have the mixed extension G = (Z
4
× Z
2
) • D
4
= K • H but
it is not a centr of G. Thus, we do not have a central extension but we have a mixed
extension. Now, we have to find the generators of [4] and store them.
NL[4] eq sub<NL[4]|NL[4].1,NL[4].2>;
A:=NL[4].1;A;
B:=NL[4].2;B;
A:=N!(1, 4, 3, 8)(2, 6, 7, 5);
B:=N!(2, 7)(5, 6);
NL4:=sub<N|A,B>;
85
The presentation for [4] is < A, B|A
4
, B
2
, (A, B) >. Now, we have to find the rest of
the group by factoring G = N by K = Z
4
× Z
2
to find H.
> q,ff:=quo<N|NL4>;
> IsAbelian(q);
false
> Center(q);
Permutation group acting on a set of cardinality 4
Order = 2
(1, 3)(2, 4)
> NumberOfGenerators(q);
6
> q eq sub<q|q.1,q.2>;
true
> q1:=q.1; q2:=q.2;
We obtain that q is a Dihedral group D
4
of order 8 because |q.1| = 4, |q.2| = 2, and
|q.1 ∗ q.2| = 2.
Since G = K • H and G/K
∼
=
H, there is a map Φ : G/K → H given by g
i
7−→ ng
i
,
where q ∈ H and Q = K ∪ Kg
1
∪ Kg
i
.
Φ :G/K −→ H,
KT [1] 7−→ Id(K),
KT [2] 7−→ q.1,
KT [3] 7−→ q.2.
In another word, let g ∈ G/K, we want to show that if g ∈ Kg
1
⇒ gg
1
−1
∈ K. This
process called ’factor sets’.
> T:=Transversal(N,NL4);
> T[1];
Id(N)
> T2:=T[2]; T2;
(1, 2)(3, 7)(4, 5, 8, 6)
> T3:=T[3]; T3;
(1, 3)(2, 5)(4, 8)(6, 7)
> T23:=T[2]
*
T[3];
> T23;
(1, 5, 4, 2, 3, 6, 8, 7)
> q.1
*
q.2;
(1, 4)(2, 3)
86
> q eq sub<q|q1,q2>;
true
> ff(T[2]) eq q1;
true
> ff(T[3]) eq q2;
true
To find the action of q1 and q2 and thier product on A and B, we use the Schreier
system then include the result in our presentation.
I:=[Id(NN): i in [1..5]];
for i in [1..8] do if ArrayP[i] eq T23ˆ2 then Sch[i];
I[1]:=Sch[i]; end if; end for;
for i in [1..8] do if ArrayP[i] eq AˆT2 then Sch[i];
I[2]:=Sch[i]; end if; end for;
for i in [1..8] do if ArrayP[i] eq BˆT2 then Sch[i];
I[3]:=Sch[i]; end if; end for;
for i in [1..8] do if ArrayP[i] eq AˆT3 then Sch[i];
I[4]:=Sch[i]; end if; end for;
for i in [1..8] do if ArrayP[i] eq BˆT3 then Sch[i];
I[5]:=Sch[i]; end if; end for;
I;
The MAGMA input for the presentation of G is
> H<x,y,z,w>:=Group<x,y,z,w|xˆ4,yˆ2,(x,y),zˆ4,wˆ2,(z
*
w)ˆ2=x,\
> xˆz=x
*
y,yˆz=xˆ2
*
y,xˆw=x
*
y,yˆw=y>;
> f,h,k:=CosetAction(H,sub<H|Id(H)>);
> #h;
64
> s:=IsIsomorphic(N,h);
> s;
true
Thus, we see that G is isomorphic to the mixed extension of Z
4
× Z
2
by D
4
.
G = N = (Z
4
× Z
2
) • D
4
.
87
5.1.2 2
•
P GL
2
(11) as a homomorphic Image of 2
∗
8
: ((Z
4
× Z
2
) • D
4
)
Consider the progenitor
2
∗
8
: N =< a, b, c, d, e, r, t|a
2
= d, b
2
, c
2
, d
2
, e
2
, r
2
, b
a
= bc, c
a
= ce, c
b
= c, d
a
= d,
d
b
= de, d
c
= dr, e
a
= er, e
b
= e, e
c
= e, e
d
= e, r
a
= r, r
b
= r, r
c
= r,
r
d
= r, r
e
= r, t
2
, (t, e), (t, ber), (t, db) >,
where N = (Z
4
×Z
2
)•D
4
. We factor the progenitor by two relations (bcet)
3
and (ebt
a
t)
5
to obtain a homomorphic image G1 of order 2640. We now prove that G1 is a central
extension of Z
2
by PGL(2,11).
The next MAGMA input code is to make sure that the kernal of the homomorphism
f : G → S
|H|
is equal to 1, so that G1 is a faithful permutation rpresentation of G.
f,G1,k:=CosetAction(G,sub<G|Id(G)>);
SL:=Subgroups(G1);
T:={X‘subgroup:X in SL};
TrivCore:={H:H in T| #Core(G1,H) eq 1};
mdeg:=Min({Index(G1,H):H in TrivCore});
Good:={H:H in TrivCore|Index(G1,H) eq mdeg};
H:=Rep(Good);
The composition series for this group is as the following:
G = G ⊇ G
1
⊇ 1, where G = (G/G
1
)(G
1
/1) = C
2
L
2
(11).
By looking at the normal lattice and checking its center, we found that we may have a
central extension since the center of G is of order 2. But, we see that the center of G
belongs to [4] which indicates that we do not have a direct product. Also, it is not a
semi direct product since the automorphism group of order 2 is 1. Thus, G is a central
extention of Z
2
by Q. To find Q, we factor G1 by the center and apply the ’factor sets’
process.
> NL[2] eq Center(G1);
true
> q,ff:=quo<G1|NL[2]>;
> H<x,y,z,w>:=Group<x,y,z,w|xˆ2,yˆ2,zˆ2,wˆ2,(x
*
y)ˆ4,
> (x
*
z)ˆ2,(x
*
w)ˆ10,(y
*
z)ˆ2,(y
*
w)ˆ2,(z
*
w)ˆ6,(x,y)ˆ2,
> (x,w)ˆ5,(z,w)ˆ3,(x
*
y
*
z)ˆ4,(x
*
y
*
w)ˆ12,(x
*
z
*
w)ˆ10,
> (xˆy
*
z)ˆ2,(xˆz
*
w)ˆ10,(x
*
y,z),(x
*
z,w)ˆ5,(x
*
y
*
z,w)ˆ5,
88
> (x
*
y
*
w,z)ˆ3,(x
*
y,z
*
w)ˆ5,(x
*
z
*
y
*
w
*
x
*
y)ˆ2,
> (x
*
w
*
z
*
y
*
w
*
x)ˆ2,(w
*
x
*
y
*
w
*
z
*
x
*
y
*
w)ˆ2,
> (x,y
*
z
*
w
*
y
*
z
*
w
*
z
*
w)ˆ2,(x
*
y
*
z
*
y
*
w)ˆ10,
> (y
*
x
*
w
*
z
*
x
*
y
*
w
*
z)ˆ5,(y,xˆz
*
y
*
z
*
w
*
z
*
x
*
y
*
w)ˆ3,
> (x
*
y
*
z
*
y
*
x
*
w
*
y
*
w
*
z
*
y
*
w
*
x)ˆ10,
> (x
*
y
*
z
*
w,y
*
z
*
x
*
w
*
y
*
z
*
w
*
y)ˆ2,(x
*
y
*
z, w
*
y
*
x)ˆ5,
> (x
*
z
*
y
*
w,w
*
x
*
z
*
y)ˆ3,
> (x
*
z
*
y
*
w
*
x
*
y
*
w
*
z
*
x
*
y
*
w
*
z
*
y
*
x
*
w)ˆ5,
> (x
*
w
*
y
*
z
*
w
*
z
*
y
*
x
*
w)ˆ5>;
> f,h,k:=CosetAction(H,sub<H|Id(H)>);
> #h;
1320
> s:=IsIsomorphic(q,h); s;
true
> T:=Transversal(G1,NL[2]);
> ff(T[2]) eq q.1;
true
> ff(T[3]) eq q.2;
true
> ff(T[4]) eq q.3;
true
> ff(T[5]) eq q.7;
true
> Order(T[2]), Order(T[3]), Order(T[4]), Order(T[5]);
4 2 2 2
> Order(q.1);
2
> T[2]ˆ2;
(1,4)(2,7)(3,9)(5,11)(6,14)(8,15)(10,17)(12,20)(13,21)
(16,24)(18,26)(19,27)(22,29)(23,30)(25,32)(28,35)(31,37)
(33,39)(34,40)(36,42)(38,43)(41,44)
> NL[2];
Permutation group acting on a set of cardinality 44
Order = 2
Id(G1)
(1, 4)(2, 7)(3, 9)(5, 11)(6, 14)(8, 15)(10, 17)(12, 20)
(13, 21)(16, 24)(18,26)(19, 27)(22, 29)(23, 30)(25, 32)
(28, 35)(31, 37)(33, 39)(34, 40)(36, 42)(38, 43)(41, 44)
> K<x,y,z,w,c>:=Group<x,y,z,w,c|xˆ2=c,yˆ2,zˆ2,wˆ2,(x
*
y)ˆ4,
(x
*
z)ˆ2=c,(x
*
w)ˆ10=c,(y
*
z)ˆ2,(y
*
w)ˆ2,(z
*
w)ˆ6,(x,y)ˆ2,
(x,w)ˆ5,(z,w)ˆ3,(x
*
y
*
z)ˆ4,(x
*
y
*
w)ˆ12,(x
*
z
*
w)ˆ10=c,
(xˆy
*
z)ˆ2=c,(xˆz
*
w)ˆ10=c,(x
*
y,z),(x
*
z,w)ˆ5,(x
*
y
*
z,w)ˆ5,
(x
*
y
*
w,z)ˆ3,(x
*
y,z
*
w)ˆ5,(x
*
z,y
*
w)ˆ6,(x
*
w,y
*
z)ˆ2,(w
*
x,y
*
z)ˆ2,
(x
*
w)ˆ2
*
y
*
z)ˆ5=c,(x
*
y
*
z
*
w)ˆ12,(x
*
y
*
(z
*
w)ˆ2)ˆ10=c,

89
(x
*
z
*
y
*
w
*
x
*
y)ˆ2,(x
*
w
*
z
*
y
*
w
*
x)ˆ2,(w
*
x
*
y
*
w
*
z
*
x
*
y
*
w)ˆ2,
(x,y
*
z
*
w
*
y
*
z
*
w
*
z
*
w)ˆ2,(x
*
y
*
z
*
y
*
w)ˆ10=c,
(y
*
x
*
w
*
z
*
x
*
y
*
w
*
z)ˆ5=c,(y,xˆz
*
y
*
z
*
w
*
z
*
x
*
y
*
w)ˆ3,
(x
*
y
*
z
*
y
*
x
*
w
*
y
*
w
*
z
*
y
*
w
*
x)ˆ10=c,(x
*
y
*
z
*
w,y
*
z
*
x
*
w
*
y
*
z
*
w
*
y)ˆ2,
(x
*
y
*
z, w
*
y
*
x)ˆ5,(x
*
z
*
y
*
w,w
*
x
*
z
*
y)ˆ3,
(x
*
z
*
y
*
w
*
x
*
y
*
w
*
z
*
x
*
y
*
w
*
z
*
y
*
x
*
w)ˆ5,(x
*
w
*
y
*
z
*
w
*
z
*
y
*
x
*
w)ˆ5=c>;
> f,kk,k:=CosetAction(K,sub<K|Id(K)>);
> #kk;
2640
> s:=IsIsomorphic(G1,kk);
> s;
true
We prove that
2
∗
8
:N
[bcet]
3
,[ebt
a
t]
5
∼
=
2
•
P GL
2
(11).
5.1.3 (A
5
× A
5
) : 4 as a homomorphic Image of 2
∗
8
: ((Z
4
× Z
2
) • D
4
)
In this section, we will construct the Cayley diagram of (A
5
× A
5
) : 4 over
((Z
4
× Z
2
) • D
4
) and prove that G
∼
=
(A
5
× A
5
) : 4.
Consider the group
G = 2
∗
8
: ((Z
4
× Z
2
) • D
4
) =< a, b, c, d, e, r, t|a
2
= d, b
2
, c
2
, d
2
, e
2
, r
2
, b
a
= bc, c
a
= ce,
c
b
= c, d
a
= d, d
b
= de, d
c
= dr, e
a
= er, e
b
= e, e
c
= e, e
d
= e, r
a
= r, r
b
= r, r
c
= r,
r
d
= r, r
e
= r, t
2
, (t, e), (t, ber), (t, db), (bcet)
5
, (ert)
3
, (a(t
r
)
c
)
4
>,
factored by [bcet]
5
, [ert]
3
, and [a(t
r
)
c
]
4
.
N = (Z
4
× Z
2
) • D
4
=< a, b, c, d, e, r >,
where
a = (12)(37)(4586).
b = (13)(25)(48)(67).
c = (14)(26)(38)(57).
d = (48)(56).
e = (27)(56).
r = (13)(27)(48)(56).
90
Let t = t
8
. So,
[bcet]
5
= 1
[bcet
8
]
5
= 1
(bce)
5
t
8
(bce)
4
t
8
(bce)
3
t
8
(bce)
2
t
8
(bce)
t
8
= 1
(18)(34)t
8
t
1
t
8
t
1
t
8
= 1
t
8
t
1
t
8
= (18)(34)t
8
t
1
.
We write t
0
instead of t
8
.
Note 5.1. If we conjugate t
0
t
1
t
0
= (10)(34)t
0
t
1
by all elements in N, we will have more
relations as the following.
t
1
t
0
t
1
= (01)(43)t
1
t
0
, t
7
t
5
t
7
= (57)(62)t
7
t
5
,
t
5
t
7
t
5
= (75)(26)t
5
t
7
, t
2
t
6
t
2
= (62)(57)t
2
t
6
,
t
6
t
2
t
6
= (26)(75)t
6
t
2
, t
3
t
0
t
3
= (03)(41)t
3
t
0
,
t
0
t
3
t
0
= (30)(14)t
0
t
3
, t
4
t
1
t
4
= (14)(30)t
4
t
1
,
t
1
t
4
t
1
= (41)(03)t
1
t
4
, t
6
t
7
t
6
= (76)(25)t
6
t
7
,
t
7
t
6
t
7
= (67)(52)t
7
t
6
, t
2
t
5
t
2
= (52)(67)t
2
t
5
,
t
5
t
2
t
5
= (25)(76)t
2
t
5
, t
3
t
4
t
3
= (43)(01)t
3
t
4
,
t
4
t
3
t
4
= (34)(10)t
4
t
3
.
[ert]
3
= 1
[ert
0
]
3
= 1
(er)
3
t
0
(er)
2
t
0
(er)
t
0
= 1
(13)(40)t
0
t
4
t
0
= 1
t
0
t
4
= (13)(40)t
0
.
Note 5.2. If we conjugate t
0
t
4
= (13)(40)t
0
by all elements in N, we will have the
following relations:
t
1
t
3
= (04)(31)t
1
, t
2
t
7
= (65)(72)t
2
, t
3
t
1
= (04)(13)t
3
,
t
4
t
0
= (13)(04)t
4
, t
5
t
6
= (72)(65)t
5
, t
6
t
5
= (27)(56)t
6
,
t
7
t
2
= (56)(27)t
7
.

91
[a(t
r
)
c
]
4
= 1
[at
1
]
4
= 1
a
4
t
1
a
3
t
1
a
2
t
1
a
t
1
= 1
t
2
t
1
t
2
t
1
= 1
t
2
t
1
= t
1
t
2
.
Note 5.3. If we conjugate t
2
t
1
= t
1
t
2
by all elements in N, we will have the following
relations:
t
4
t
5
= t
5
t
4
, t
4
t
7
= t
7
t
4
, t
4
t
6
= t
6
t
4
, t
6
t
0
= t
0
t
6
,
t
5
t
0
= t
0
t
5
, t
6
t
1
= t
1
t
6
, t
7
t
0
= t
0
t
7
, t
7
t
1
= t
1
t
7
,
t
2
t
3
= t
3
t
2
, t
3
t
7
= t
7
t
3
, t
0
t
2
= t
2
t
0
, t
2
t
4
= t
4
t
2
,
t
1
t
5
= t
5
t
1
, t
3
t
6
= t
6
t
3
, t
5
t
3
= t
3
t
5
, t
3
t
6
= t
6
t
3
.
The double coset enumeration:
• Consider N eN which is denoted by [∗].
The number of right cosets in [∗] =
|N|
|N|
=
64
64
= 1.
The orbit of N on {0,1,2,3,4,5,6,7} is {0,1,2,3,4,5,6,7}.
Pick a representative from the orbit {0,1,2,3,4,5,6,7}, say 0, and determine the
double coset that contain Nt
0
.
[0]:
• Consider N t
0
N which is denoted by [0].
N
0
= h(27)(56), (13)(2576), (25)(67)i = N
(0)
.
The number of right cosets in [0] =
|N|
|N
(0)
|
=
64
8
= 8.
The orbits of N
(0)
on {0,1,2,3,4,5,6,7} are {0}, {4}, {1,3} and {2,5,6,7}.
Nt
0
t
0
∈ [∗] (1 symmetric generator goes back to the double coset [∗]).
Nt
0
t
4
∈ [04]. Nt
0
t
1
∈ [01]. Nt
0
t
2
∈ [02].
• Consider N t
0
t
1
N which is denoted by [01].
N
01
= h(27)(56), (26)(57)i = N
(01)
.
The number of the right cosets in [01] is equal to
|N|
|N
(01)
|
=
64
4
= 16.
The orbits of N
(01)
on {0,1,2,3,4,5,6,7} are {0}, {1}, {3}, {4}, and {2,5,6,7}.

92
Nt
0
t
1
t
0
∈ [010].
Nt
0
t
1
t
1
= Nt
0
(1 symmetric generator goes back to the double coset [0]).
Nt
0
t
1
t
3
∈ [013].
Nt
0
t
1
t
4
∈ [014].
Nt
0
t
1
t
2
∈ [012].
• Consider N t
0
t
2
N which is denoted by [02].
N
02
= h(13)(56)i. The right cosets in [02] are not distinct. From previous rela-
tions, we know that Nt
0
t
2
= Nt
2
t
0
.
Therefore, N
(02)
= {n ∈ N|N(020)
n
= N(02)}.
N(02)
(1635)(20)(47)
= N20 = N02.
N(02)
(1536)(20)(47)
= N20 = N02.
Thus, (1635)(20)(47), (1536)(20)(47) ∈ N
(02)
and
N
(02)
≥ h(13)(56), (1635)(20)(47), (1536)(20)(47)i = N
(02)
.
The number of right cosets in [02] =
|N|
|N
(02)
|
=
64
4
= 16.
The orbits of N
(02)
on {0,1,2,3,4,5,6,7} are {0,2}, {4,7}, and {1,3,5,6}.
Nt
0
t
2
t
2
= Nt
0
(1 symmetric generator goes back to the double coset [0]).
Nt
0
t
2
t
4
∈ [024].
Nt
0
t
2
t
1
∈ [021].
• Consider N t
0
t
4
N which is denoted by [04].
Because the relation
Nt
0
t
4
= N(13)(40)t
0
= Nert
0
= Nt
0
.
where Nt
0
∈ [0].
There exist {n ∈ N|N(t
0
)
n
= Nt
0
}.
Thus, N(t
0
)
e
= Nt
0
. Nt
0
t
4
∈ [0].
Therefore, Nt
0
t
4
N is not a new double coset and collapses ⇒ one symmetric
genertator will take back to [0].

93
[01]:
• Consider N t
0
t
1
t
0
N which is denoted by [010].
Because the relation
Nt
0
t
1
t
0
= N(10)(34)t
0
t
1
= Nbcet
0
t
1
= Nt
0
t
1
where Nt
0
t
1
∈ [01].
There exist {n ∈ N|N(t
0
t
1
)
n
= Nt
0
t
1
}.
Thus, N(t
0
t
1
)
e
= Nt
0
t
1
. Nt
0
t
1
t
0
∈ [01].
Therefore, N t
0
t
1
t
0
N is not a new double coset and collapses ⇒ one symmetric
genertator will go back to [01].
• Consider N t
0
t
1
t
2
N which is denoted by [012].
N
012
= hei = N
(012)
.
The number of right cosets in [012] =
|N|
|N
(012)
|
=
64
1
= 64.
The orbits of N
(012)
on {0,1,2,3,4,5,6,7} are {0}, {1}, {2}, {3}, {4}, {5}, {6} and
{7}.
Nt
0
t
1
t
2
t
0
∈ [0120].
Nt
0
t
1
t
2
t
1
∈ [0121].
Nt
0
t
1
t
2
t
2
= Nt
0
t
1
(1 symmetric generator goes back to the double coset [01].
Nt
0
t
1
t
2
t
3
∈ [0123]. Nt
0
t
1
t
2
t
4
∈ [0124]. Nt
0
t
1
t
2
t
5
∈ [0125]. Nt
0
t
1
t
2
t
6
∈ [0126].
Nt
0
t
1
t
2
t
7
∈ [0127].
• Consider N t
0
t
1
t
3
N which is denoted by [013].
Because of the relation
Nt
0
t
1
t
3
= Nt
0
(84)(31)t
1
= N(84)(31)t
4
t
1
= Nert
0
t
1
(48)(56)
where Nt
4
t
1
∈ [01].
There exist {n ∈ N|N(t
0
t
1
)
n
= Nt
4
t
1
}.
Thus, N(t
0
t
1
)
(48)(56)
= Nt
4
t
1
. Nt
0
t
1
t
3
∈ [01].
Therefore, N t
0
t
1
t
3
N is not a new double coset and collapses ⇒ one symmetric
genertator will take back to [01].

94
• Consider N t
0
t
1
t
4
N which is denoted by [014].
N
014
= h(27)(56), (25)(67)i.
The right cosets in [014] are not distinct. By using the above relations, we obtain
the following
Nt
0
t
1
t
4
= Nt
0
(41)(03)t
1
t
4
t
1
= N(41)(03)t
3
t
1
t
4
t
1
= N(41)(03)(04)(13)t
3
t
4
t
1
= N(01)(34)t
3
t
4
t
1
.
Nt
0
t
1
t
4
= Nt
0
t
1
(13)(04)t
4
t
0
= N(13)(04)t
4
t
3
t
4
t
0
= N(13)(04)(10)(34)t
4
t
3
t
0
= N(14)(03)t
4
t
3
t
0
.
Nt
0
t
1
t
4
= N(10)(34)t
0
t
1
t
0
t
4
= N(10)(34)t
0
(04)(13)t
1
t
3
t
0
t
4
= N(14)(03)t
4
t
1
t
3
t
0
t
4
= N(14)(03)t
4
t
1
t
3
(13)(04)t
0
= N(01)(34)t
0
t
3
t
1
t
0
= N(01)(34)t
0
t
3
t
1
(03)(14)t
0
t
3
t
0
t
3
= (13)(04)t
3
t
0
t
4
t
0
t
3
t
0
t
3
= N(13)(04)t
3
(13)(04)t
3
t
0
t
3
= Nt
1
t
3
t
0
t
3
= N(04)(13)t
1
t
0
t
3
.
Hence, Nt
0
t
1
t
4
= Nt
3
t
4
t
1
= Nt
4
t
3
t
0
= Nt
1
t
0
t
3
.
Therefore, N
(014)
= {n ∈ N|N(014)
n
= N(014)}.
N(014)
(13)(25)(40)(67)
= N430 = N014.
N(014)
(13)(26)(40)(57)
= N430 = N014.
N(014)
(13)(27)(40)(56)
= N430 = N014.
N(014)
(13)(40)
= N430 = N014.
N(014)
(14)(26)(30)(57)
= N341 = N014.
N(014)
(14)(25)(30)(67)
= N341 = N014.
N(014)
(14)(30)
= N341 = N014.
N(014)
(14)(27)(30)(56)
= N341 = N014.
N(014)
(10)(27)(34)(56)
= N103 = N014.
N(014)
(10)(34)
= N341 = N014.
N(014)
(10)(25)(34)(67)
= N103 = N014.
N(014)
(10)(26)(34)(57)
= N103 = N014.

95
Thus, all the above permutation are in N
(014)
and N
(014)
= N
(014)
.
The number of right cosets in [014] =
|N|
|N
(014)
|
=
64
16
= 4.
The orbits of N
(014)
on {0,1,2,3,4,5,6,7} are {0,1,3,4} and {2,5,6,7}.
Nt
0
t
1
t
4
t
4
= Nt
0
t
1
(4 symmetric generators go back to the double coset [01]).
Nt
0
t
1
t
4
t
2
∈ [0142].
[02]:
• Consider N t
0
t
2
t
1
N which is denoted by [021].
Because of the relation
Nt
0
t
2
t
1
= Nt
0
t
1
t
2
.
There exist {n ∈ N|N(t
0
t
1
t
2
)
n
= Nt
0
t
1
t
2
}.
Thus, N(t
0
t
1
t
2
)
e
= Nt
0
t
1
t
2
.
Therefore, Nt
0
t
2
t
1
N is not a new double coset and collapses ⇒ four symmetric
genertators will take to [012].
• Consider N t
0
t
2
t
4
N which is denoted by [024].
Because of the relation
Nt
0
t
2
t
4
= Nt
0
t
4
t
2
= N(13)(40)t
0
t
2
= Nert
0
t
2
.
There exist {n ∈ N|N(t
0
t
2
)
n
= Nt
0
t
2
}.
Thus, N(t
0
t
2
)
id
= Nt
0
t
2
.
Therefore, Nt
0
t
2
t
4
N is not a new double coset and collapses ⇒ four symmetric
genertators will go back to [02].
[012]:
• Consider N t
0
t
1
t
2
t
0
N which is denoted by [0120].
Because of the relation
Nt
0
t
1
t
2
t
0
= Nt
0
t
1
t
0
t
2
= N(18)(34)t
0
t
1
t
2
= Nbcet
0
t
1
t
2
= Nt
0
t
1
t
2
.

96
There exist {n ∈ N|N(t
0
t
1
t
2
)
n
= Nt
0
t
1
t
2
}.
Thus, N(t
0
t
1
t
2
)
id
= Nt
0
t
1
t
2
.
Therefore, Nt
0
t
1
t
2
t
0
N is not a new double coset and collapses ⇒ one symmetric
genertator will go back to [012].
• Consider N t
0
t
1
t
2
t
1
N which is denoted by [0121].
Because of the relation
Nt
0
t
1
t
2
t
1
= Nt
0
t
1
t
1
t
2
= Nt
0
t
2
.
There exist {n ∈ N|N(t
0
t
2
)
n
= Nt
0
t
2
}.
Thus, N(t
0
t
2
)
id
= Nt
0
t
2
.
Therefore, Nt
0
t
1
t
2
t
1
N is not a new double coset and collapses ⇒ one symmetric
genertator will go back to [02].
• Consider N t
0
t
1
t
2
t
3
N which is denoted by [0123].
Because of the relation
Nt
0
t
1
t
2
t
3
= Nt
0
t
1
t
3
t
2
= Nt
0
(84)(31)t
1
t
2
= N(84)(31)t
4
t
1
t
2
= Nert
4
t
1
t
2
= Ner[t
0
t
1
t
2
]
(48)(56)
where Nt
4
t
1
t
2
∈ [012].
There exist {n ∈ N|N(t
0
t
1
t
2
)
n
= Nt
4
t
1
t
2
}.
Thus, N(t
0
t
1
t
2
)
(48)(56)
= Nt
4
t
1
t
2
.
Therefore, Nt
0
t
1
t
2
t
3
N is not a new double coset and collapses ⇒ one symmetric
genertator will go back to [012].
We now continue the double coset enumeration by proceding in this manner
until the set of right cosets is closed under right multiplication by t
0
i
s where i = 0, · · · , 7

97
. Thus, by finding out all of the 11 double cosets [w], we can determine the index of N
in G. We conclude that
|G| ≤ (|N| +
|N|
|N
(0)
|
+
|N|
|N
(01)
|
+ . . . +
|N|
|N
(01246)
|
+
|N|
|N
(012457)
|
) × |N|
|G| ≤ (1 + 8 + 16 + 16 + 46 + 4 + 16 + 64 + 16 + 16 + 4) × 64
|G| ≤ (225 × 64)
|G| ≤ 14400
Next, we consider that G = ht
0
, a, b, c, d, e, ri acts on the 11 cosets and the actions of
t, a, b, c, d, e, r on the 11 cosets is well-defined. Thus, we have a homomorphism f : 2
∗
8
:
N −→ S
64
. Then f(2
∗
8
: N) =< f(a), f (b), f (c), f(d), f(e), f(r), f(t) >; that is, the
homomorphic image of G is of the order, | < f(a), f(b), f(c), f(d), f (e), f(r), f(t) > | =
14400. Since t has exactly 8 conjugates, we have f(G)
∼
=
< f(a), f(b), f(c), f(d), f(e), f (r), f(t) >,
where
f(a) = (2, 3, 4, 6)(5, 7)(8, 10) . . . (199, 216, 206, 219)(222, 223, 224, 225).
f(b) = (2, 4)(3, 7)(5, 10)(6, 8) . . . (208, 220)(210, 221)(211, 212).
f(c) = (2, 5)(3, 8)(4, 10)(6, 7) . . . (207, 211)(215, 221)(218, 220).
f(d) = (2, 4)(3, 6)(9, 18)(11, 23) . . . (220, 221)(222, 224)(223, 225).
f(e) = (3, 6)(7, 8)(9, 12)(13, 14) . . . (203, 206)(205, 211)(207, 212).
f(r) = (2, 4)(3, 6)(5, 10)(7, 8) . . . (207, 212)(208, 220)(210, 221).
f(t) = (1, 2)(3, 9)(5, 11)(6, 12) . . . (215, 217)(216, 224)(220, 225).
Hence,
G/Ker
f
∼
=
< f(a), f(b), f(c), f(d), f(e), f (r), f(t) >= f(G)
|G/Ker
f
|
∼
=
|f(G)|
|G| ≥ |f(G)|
|G| ≥ 14400.

98
But from above we observed that |G| ≤ 14400. Hence,
⇒ |G| = 14400
⇒ Kerf = 1
⇒ G
∼
=
< f(a), f(b), f(c), f(d), f(e), f (r), f(t) >
⇒ G
∼
=
S
64
.
G =
2
∗
8
:N
[bcet]
5
,[ert]
3
,[a(t
r
)
c
]
4
Please see the Cayley diagram of (A
5
× A
5
) : 4 over (Z
4
× Z
2
) • D
4
below.
Figure 5.1: Cayley Diagram for (A
5
× A
5
) : 4 Over (Z
4
× Z
2
) • D
4
We now show that G
∼
=
(A
5
× A
5
) : 4.
G =< a, b, c, d, e, r, t|a
2
= d, b
2
, c
2
, d
2
, e
2
, r
2
, b
a
= bc, c
a
= ce, c
b
= c, d
a
= d, d
b
= de,
d
c
= dr, e
a
= er, e
b
= e, e
c
= e, e
d
= e, r
a
= r, r
b
= r, r
c
= r, r
d
= r, r
e
= r, t
2
,
(t, e), (t, ber), (t, db), (bcet)
5
, (ert)
3
, (a(t
r
)
c
)
4
> .
By using MAGMA, we have the composition series G ⊇ G
1
⊇ G
2
⊇ G
3
⊇ 1, where
G = (G/G
1
)(G
1
/G
2
)(G
2
/G
3
)(G
3
/1) = C
2
C
2
A
5
A
5
.
The normal lattice of G is

99
Figure 5.2: The Normal Lattice of (A
5
× A
5
) : 4
We want to determine the isomorphism type of this group. We find that the center of
G is of order 1. So, this is not a central extension. Moreover, by looking at the normal
lattice of G, we see that it does not have a normal subgroup of order 2. Thus, this is
not a direct product. The order of the minimal normal subgroup is 3600 which indicate
that we have a direct product of A
5
by A
5
.
> H<a,b,c,d>:=Group<a,b,c,d|aˆ3,bˆ2,(a
*
b)ˆ5,cˆ3,dˆ2,
(c
*
d)ˆ5,(a,c),(a,d),(b,c),(b,d)>;
> f,H1,k:=CosetAction(H,sub<H|Id(H)>);
> #H;
3600
> s,t:=IsIsomorphic(H1,NL[2]);
> s;
true
Thus, we have shown G
2
= A
5
× A
5
= [2]. Since the normal lattice of [3] and [4] do not
contain a normal subgroup of order 4, it is not a direct product with C
2
2
= C
4
. Now,
we want to check if it is a semi-direct product of [2] by C
4
. We find that it is. Thus, we
have A
5
× A
5
extended by C
4
. Then, we must find the action of C
4
on the generators
of A
5
× A
5
. We compute the action of e on a, b, c, and d by using the Schreier System
for A
5
× A
5
and write a presentation for (A
5
× A
5
) : 4.
> HH<a,b,c,d,e>:=Group<a,b,c,d,e|aˆ3,bˆ2,(a
*
b)ˆ5,cˆ3,dˆ2,
(c
*
d)ˆ5,(a,c),(a,d),(b,c),(b,d),eˆ4,aˆe=d
*
cˆ-1
*
d
*
c
*
d
*
c,
bˆe=d
*
c
*
d
*
cˆ-1
*
d,cˆe=b
*
aˆ-1
*
b
*
a
*
b
*
a,dˆe=a
*
b
*
a
*
b
*
aˆ-1
*
b
*
aˆ-1>;
100
> f2,H2,k2:=CosetAction(HH,sub<HH|Id(HH)>);
> #HH;
14400
> s:=IsIsomorphic(H2,G1);
> s;
true
5.1.4 S
5
as a Homomorphic Image of G over N
G =< a, b, c, d, e, r, t|a
2
= d, b
2
, c
2
, d
2
, e
2
, r
2
, b
a
= bc, c
a
= ce, c
b
= c, d
a
= d, d
b
= de,
d
c
= dr, e
a
= er, e
b
= e, e
c
= e, e
d
= e, r
a
= r, r
b
= r, r
c
= r, r
d
= r, r
e
= r, t
2
,
(t, e), (t, ber), (t, db), (dbt
c
)
2
, (ert)
2
, (a(t
r
)
c
)
5
, (ct
b
)
3
> .
By using MAGMA, we have the composition series G ⊇ G
1
⊇ 1, where
G = (G/G
1
)(G
1
/1) = C
2
A
5
.
We want to determine the isomorphism type of this group. This group is not a central
extension since the center of G is of order 1. Moreover, by looking at the normal lattice
of G, we see that it does not have a normal subgroup of order 2. So, this is not a direct
product. The order of the minimal normal subgroup is 60 which indicate that we have a
semi-direct product of [2]=A
5
by Z
2
. Using MAGMA, we highlight the relation between
them by finding the generators A and B of A
5
and write the action of an element C of
order 2 on A and B by using Scherier system to write a presentation for A
5
: C
2
∼
=
S
5
.
> a:=NL[2].1;
> b:=NL[2].2;
> HH<a,b,c>:=Group<a,b,c|aˆ2,bˆ3,(a
*
b)ˆ5,cˆ2,
aˆc=bˆ-1
*
a
*
bˆ-1
*
a
*
b
*
a
*
b,bˆc=a
*
b
*
a
*
bˆ-1
*
a
*
bˆ-1>;
> #HH;
120
> f2,H2,k:=CosetAction(HH,sub<HH|Id(HH)>);
> s:=IsIsomorphic(H2,G1); s;
true
> s:=IsIsomorphic(H2,Sym(5)); s;
true
Thus, we have shown that G
∼
=
S
5
.

101
5.2 The Progenitor 2
∗
14
: (L
2
(7) × 2)
A presentation for the progenitor for the transitive group on 14 letters is
< a, b, t|a
7
, b
6
, (a
−1
b
−1
)
2
, (ab
−2
)
2
, (ab
−1
a)
4
, t
2
, (t, b
2
), (t, a
2
b
2
a) >
In order to find finite images, we factored the progenitor at first by all of the first order
relations using the conjugacy classes of N = L
2
(7) × 2 (see table 5.2) with a relation
that have found by Lemma (tt
a
−2
b
)
k
= b
a
b
−1
a
3
but it did not produce any images.
Table 5.2: Conjugacy Classes of L
2
(7) × 2
Class Representitive of the class 1
st
order relations
C
1
identity
C
2
b
3
b
3
t
1
C
3
ab abt
1
,abt
2
,abt
10
C
4
(ab
−1
a)
2
(ab
−1
a)
2
t
1
,(ab
−1
a)
2
t
4
,(ab
−1
a)
2
t
10
C
5
b
2
b
2
t
1
,b
2
t
2
,b
2
t
7
C
6
ba
2
b
2
a ba
2
b
2
at
1
,ba
2
b
2
at
4
,ba
2
b
2
at
10
C
7
b
2
a
2
b
2
a
2
t
1
,b
2
a
2
t
7
,b
2
a
2
t
11
C
8
b bt
1
,bt
2
,bt
7
C
9
a at
1
C
1
0 a
3
a
3
t
1
C
1
1 ab
−1
ab
−1
t
1
C
1
2 aba
−1
bab
−1
aba
−1
bab
−1
t
1
Thus, we tried to run the progenitor given above that have been factored just
by the following first order relations. Then, we labeled the result in the table below.
(b
3
t)
l
, (abt)
m
, (abt
a
)
n
, (abt
a
4
)
o
, ((ab
−1
a)
2
t)
p
, ((ab
−1
a)
2
t
a
4
)
q
, ((ab
−1
a)
2
t
a
2
)
r
, (b
2
t)
s
,
(b
2
t
a
)
u
, (b
2
t
a
3
)
v
, (ba
2
b
2
at)
w
, (ba
2
b
2
at
a
2
)
x
, (ba
2
b
2
at
a
4
)
y
, (b
2
a
2
t
a
5
)
z
, (b
2
a
2
t
a
3
)
c
,
(b
2
a
2
t)
d
, (bt)
e
, (bt
a
)
f
, (bt
a
3
)
g
, (at)
i
, (a
3
t)
j
, (ab
−1
t)
h
, (aba
−1
bab
−1
t)
qq
.
Table 5.3: Some finite images of the Progenitor 2
∗
14
: [L
2
(7) × 2]
k l · · · j h qq Index in G Order of G Shape of G
0 0 · · · 6 6 6 270 90720 3
2
• (S
7
× 2)
0 0 · · · 7 7 7 512 86016 4
3
• (2
3
: L
2
(7))

102
5.3 The Progenitor 2
∗
16
: (2
4
: A
5
)
A presentation for 2
4
: A
5
is
< a
3
, b
4
, b
−1
a
−1
b
−2
a
−1
b
2
a
−1
b
−1
, (b
−1
a
−1
)
5
, (b
−1
a)
5
,
a
−1
b
−1
a
−1
ba
−1
b
−1
a
−1
b
−1
abab
2
a
−1
bab > .
and a presentation for 2
∗
16
: (2
4
: A
5
) is
< a, b, t|a
3
, b
4
, b
−1
a
−1
b
−2
a
−1
b
2
a
−1
b
−1
, (b
−1
a
−1
)
5
, (b
−1
a)
5
,
a
−1
b
−1
a
−1
ba
−1
b
−1
a
−1
b
−1
abab
2
a
−1
bab, t
2
, (t, a
−1
b
−1
a
−1
bab),
(t, ab
−1
abab
−1
a), (t, ab
−1
a
−1
b
−1
abab
−1
), (t, a
−1
ba
−1
b
−1
a
−1
bab) > .
We factored the progenitor by all of the first order relations that have been found by
the conjugacy classes of N = 2
4
: A
5
(see table 5.4).
Table 5.4: Conjugacy Classes of 2
4
: A
5
Class Representitive of the class 1
st
order relations
C
1
identity
C
2
b
2
b
2
t
1
C
3
aba
−1
baba
−1
b
2
aba
−1
baba
−1
b
2
t
i
, where i = 1, 2, 3, 5
C
4
bab babt
1
,babt
2
,babt
3
,babt
4
,babt
11
,babt
13
C
5
b bt
1
C
6
ba
−1
b
−1
ab ba
−1
b
−1
abt
1
C
7
ab
−1
aba
−1
b
−1
ab ab
−1
aba
−1
b
−1
abt
1
C
8
ba bat
1
,bat
2
,bat
4
,bat
5
C
9
(ba)
2
(ba)
2
t
1
,(ba)
2
t
2
,(ba)
2
t
4
,(ba)
2
t
5
The all of the first order relations are
(b
2
t)
v
, (aba
−1
baba
−1
b
2
t)
l
, (aba
−1
baba
−1
b
2
t
b
)
m
, (aba
−1
baba
−1
b
2
t
ba
)
n
,
(aba
−1
baba
−1
b
2
(t
ba
)
a
)
o
, (babt)
p
, (babt
b
)
q
, (babt
ba
)
r
, (babt
b
2
)
s
, (babt
b
−1
a
)
u
, (babt
b
2
)
a
−1
)
w
,
(bt)
x
, (ba
−1
b
−1
abt)
y
, (ab
−1
aba
−1
b
−1
abt)
z
, (bat)
c
, (bat
b
)
d
, (bat
b
2
)
e
, (ba(t
ba
)
a
)
f
, ((ba)
2
t)
g
,
((ba)
2
t
b
)
h
, ((ba)
2
t
b
2
)
i
, ((ba)
2
(t
ba
)
a
)
j
.
When we factored the progenitor by all of the first order relations, no interesting ho-
momorphic images were found. Thus, we change the relators to
(aba
−1
bab
−1
abt)
k
, (ab
−1
a
2
t)
l
, (at
(
b
3
))
m
, (b
2
a
−1
t)
n
, (a
b
tt
a
)
o
, ((ab)
2
tt
b
−1
)
p
103
The following images were obtained.
Table 5.5: Some finite images of the Progenitor 2
∗
16
: (2
4
: A
5
)]
k l m n o p Index in G Order of G Shape of G
0 0 0 6 3 10 64 61440 2
6
• (2
4
: A
5
)
0 0 0 6 3 5 32 30720 2
8
• (2 × A
5
)
5.4 The Progenitor 2
∗
4
: (2
2
: 3)
A presentation for the progenitor is
< a, b, c, t|a
3
, b
2
, c
2
, b
a
= c, c
a
= bc, c
b
= c, t
2
, (t, ac) >
By applying the lemma, we got the following
G =
2
∗
4
:(2
2
:3)
[bct]
5
=1
∼
=
3 × L
2
(11), where t ≈ t
4
.
To have more images as tabulated in Table 5.6, we factored the progenitor by the
following relators (bct)
k
, (ba
2
t)
q
, (a
−1
cbtt
c
)
u
, and (at
c
)
v
.
Table 5.6: Some finite images of the Progenitor 2
∗
4
: (2
2
: 3)
k q u v Index in G Order of G Shape of G
2 6 3 6 2 24 2
3
: 3
5 11 11 11 55 660 L
2
(11)
6 4 2 4 10 120 A
5
: 2
∼
=
S
5
6 6 3 6 54 648 3
3
• (A
4
× 2)
7 7 7 7 91 1092 L
2
(13)
10 6 3 6 250 3000 5
3
• (A
4
× 2)
14 6 3 6 686 8232 7
3
• (A
4
× 2)
22 6 3 6 2662 31944 11
3
• (A
4
× 2)
6 8 4 8 640 7680 4 • (2
4
: S
5
)
4 6 3 6 16 192 2
4
: A
4
20 6 3 6 2000 24000 (2
3
× 5
3
) • (A
4
× 2)
12 6 3 6 432 5184 (2
3
× 3
3
) • (A
4
× 2)
18 6 3 6 1458 17496 9
3
• (A
4
× 2)
16 6 3 6 1024 12288 8
3
• (A
4
× 2)
24 6 3 6 3456 41472 (4
3
× 3
3
) : (A
4
× 2)
8 6 3 6 128 1536 4
3
• (A
4
× 2)

104
5.5 The Progenitor 2
∗
6
: (3
2
: 2
2
)
A presentation for the progenitor is
< a, b, c, d, t|a
2
, b
2
, c
3
, d
3
, b
a
= b, c
a
= c, c
b
= c
2
, d
a
= d
2
, d
b
= d, d
c
= d,
t
2
, (t, dc
−1
), (t, abc
−1
d
−1
) >,
where t ≈ t
6
. The tabulated homomorphic images were obtained by factoring the
progenitor 2
∗
6
: (3
2
: 2
2
) by
(ad
−1
t)
k
, (a
−1
dt)
w
, (cd
2
tt
b
)
x
, (bctt
d
)
y
Table 5.7: Some finite images of the progenitor 2
∗
6
: (3
2
: 2
2
)
k w x y Index in G Order of G Shape of G
0 0 3 6 162 5832 (9 × 3
2
) : [(2
2
× 3) : 2]
0 0 3 2 18 648 3
3
: [(3 × 2
2
) : 2]
0 0 5 2 10 40 (2
2
× 5) : 2
0 0 9 2 54 1944 (9 × 3
2
) • [(2
2
× 3) : 2]
0 0 12 2 72 2592 (4 × 3
3
) • [(2
2
× 3) : 2]
5.6 The Progenitor 2
∗
10
: [(2 × 5) : 4]
A presentation for the progenitor is
< a, b, c, d, t|a
2
= c, b
2
, c
2
, d
5
, b
a
= b, c
a
= c, c
b
= c, d
a
= d
2
, d
b
= d, d
c
= d
4
,
t
2
, (t, cd), (t, ba
−1
d
−1
) >,
where t ≈ t
10
. The tabulated homomorphic images were obtained by factoring the
progenitor 2
∗
10
: [(2 × 5) : 4] by the following relators
(ad
3
at)
k
, (cabt
b
)
h
, (d
2
tt
a
)
i
, (a
2
t
c
)
j

105
Table 5.8: Some finite images of the Progenitor 2
∗
10
: [(2 × 5) : 4]
k h i j Index in G Order of G Shape of G
2 30 2 6 432 17280 (2
2
× 3) • (P GL
2
(9) : 2)
4 5 2 6 36 1440 P GL
2
(9) : 2
0 0 30 2 60 2400 (4 × 3 × 5
2
) : (4 × 2)
4 6 2 15 360 14400 A
5
× A
5
: 2
2
4 15 2 6 108 4320 3 • [P GL
2
(9) : 2]
0 0 2 6 864 34560 (4 × 2 × 3) • (P GL
2
(9) : 2)
0 4 3 10 750 30000 5
4
: [(4 × 2 × 3) : 2]
4 10 2 6 144 5760 2
2
: (P GL
2
(9) : 2)
4 6 2 30 2880 115200 2
3
• [(A
5
× A
5
) : 2
2
]
6 8 2 8 288 11520 (4 × 2) : (P GL
2
(9) : 2)
6 7 2 8 4032 161280 2 • ([L
3
(4) : 2] : 2)
106
Chapter 6
Wreath Product of Permutation
Group
6.1 Preliminaries
Definition 6.1 (Wreath Product). Let H and K be permutation groups on X and
Y , respectively, and let Z = X × Y . We define below a permutation group on Z =
{(x, y)|x ∈ X, y ∈ Y }, called the wreath product of H by K denoted by H o K.
Note 6.2. Apermutation group on Z denoted by S
Z
.
For the following examples, consider H = Z
2
=< (1, 2) > and K = Z
2
=< (3, 4) >.
Example 6.3. We have
• H = {1, (1, 2)} and K = {1, (3, 4)}.
• X = {1, 2} and Y = {3, 4}.
• Z = {(x, y)|x ∈ X, y ∈ Y } = {
1
(1, 3),
2
(1, 4),
3
(2, 3),
4
(2, 4)}.
Definition 6.4. Let γ ∈ H and y ∈ Y be a fixed element of Y . Then,
γ(y) =
(x, y) 7→ ((x)γ, y).
(x, y
1
) 7→ (x, y
1
) if y
1
6= y.

107
Example 6.5. Let γ = (1, 2) ∈ H and y = 3 ∈ Y . Then, γ(y) = (1, 3) found by the
following table
1 2 3 4
(1,3) (1,4) (2,3) (2,4)
↓ ↓ ↓ ↓
(2,3) (1,4) (1,3) (2,4)
3 2 1 4
Definition 6.6. Let k ∈ K. Define k
∗
: (x, y) 7→ (x, (y)k).
Note 6.7. K acting only on the second component y
i
’s.
Example 6.8. Let k = (3, 4) ∈ K. Then, k
∗
= (1, 3)
∗
= (1, 2)(3, 4) found by the
following table
1 2 3 4
(1,3) (1,4) (2,3) (2,4)
↓ ↓ ↓ ↓
(1,4) (1,3) (2,4) (2,3)
2 1 4 3
Note 6.9. If γ(y) and k
∗
are permutations of S
Z
, then
1. There is a homomorphism map φ : H → S
Z
which it is also 1-1 given by γ 7→ γ(y).
2. φ(y) = {γ(y)|γ ∈ H}.
Also,
1. There is a homomorphism map Ψ : K → S
Z
which it is also 1-1 given by k 7→ k
∗
.
2. Ψ(K) = {k
∗
|k ∈ K} = K
∗
.
The semi-direct product H
n
: K is the wreath product of H by K, where
• n is the number of letters on which H acts.

108
• H
n
is the direct product (< H
1
> × . . . × < H
n
>) of n copies permutations of
H.
In the semi-direct part, K permutates the n copies of H. Thus,
H o K = hH(y), k
∗
i =
Q
y∈Y
H(y) : K
∗
.
6.2 The Progenitor 2
∗
6
: Z
3
o Z
2
Consider the wreath product of H = Z
3
by K = Z
2
, denoted by Z
3
o Z
2
. In
the semi-direct Z
2
3
: Z
2
, Z
2
permutes the 2 copies of Z
3
. Thus, we have
Z
3
o Z
2
= Z
2
3
: Z
2
= (Z
3
× Z
3
) : Z
2
Now, we want to write a presentation for 2
∗
6
: Z
3
o Z
2
.
Z
3
o Z
2
= Z
3
× Z
3
: Z
2
.
= h(1, 2, 3)i × h(4, 5, 6)i : h(7, 8)i.
Also, we have
X = {1, 2, 3} and Y = {4, 5}.
H = h(1, 2, 3)i = hγi and K = h(4, 5)i.
Hence,
Z = X × Y = {
1
(1, 4),
2
(1, 5),
3
(2, 4),
4
(2, 5),
5
(3, 4),
6
(3, 5)}.
Now, we want to compute γ(4) and γ(5).
Table 6.1: γ(4)
1 2 3 4 5 6
(1,4) (1,5) (2,4) (2,5) (3,4) (3,5)
↓ ↓ ↓ ↓ ↓ ↓
(2,4) (1,5) (3,4) (2,5) (1,4) (3,5)
3 2 5 4 1 6
Thus, we get γ(4) = (135) = H(4).

109
Table 6.2: γ(5)
1 2 3 4 5 6
(1,4) (1,5) (2,4) (2,5) (3,4) (3,5)
↓ ↓ ↓ ↓ ↓ ↓
(1,4) (2,5) (2,4) (3,5) (3,4) (1,5)
1 4 3 6 5 2
Thus, we get γ(5) = (246) = H(5).
Then, we want to compute k
∗
= (45)
∗
.
Table 6.3: k
∗
1 2 3 4 5 6
(1,4) (1,5) (2,4) (2,5) (3,4) (3,5)
↓ ↓ ↓ ↓ ↓ ↓
(1,5) (1,4) (2,5) (2,4) (3,5) (3,4)
2 1 4 3 6 5
Thus, we get k
∗
= (45)
∗
= (12)(34)(56).
Since Z
3
o Z
2
= hH(4), H(5), k
∗
i, we obtain
Z
3
o Z
2
= h(135), (246), (12)(34)(56)i
= h(135)i × h(246)i : h(12)(34)(56)i,
where a = (135), b = (246), and c = (12)(34)(56).
To write the general presentaion for Z
3
o Z
2
, we have to find the action of c on a and b.
a
c
= (135)
(12)(34)(56)
= (246) = b.
b
c
= (246)
(12)(34)(56)
= (135) = a.
Thus, the general presentaion for Z
3
o Z
2
is
< a, b, c|a
3
, b
3
, (a, b), c
2
, a
c
= b, b
c
= a >
The order of the wreath product is |Z
3
o Z
2
| = 3 × 3 × 2 = 18. To write a progenitor for
the wreath product, we have to find a faithful permutation representation for Z
3
o Z
2
.
The next MAGMA code confirm our presentation.

110
> W:=WreathProduct(CyclicGroup(3),CyclicGroup(2));
> S:=Sym(6);
> aa:=S!(4, 5, 6);
> bb:=S!(1, 2, 3);
> cc:=S!(1, 5)(2, 6)(3, 4);
> N:=sub<S|aa,bb,cc>;
> N eq W;
true
Let t = t
1
. Now, by looking at the 18 elements of N = Z
3
o Z
2
, we have to determine the
permutation of N that fix the coset stabiliser Nt
1
. The desired permutations are the
identity and a = (4, 5, 6). By using MAGMA, we find that t commute with a. Thus,
the presentation for the progenitor 2
∗
6
: Z
3
o Z
2
is given by
< a, b, c, t|a
3
, b
3
, (a, b), c
2
, a
c
= b, b
c
= a, t
2
, (t, a) > .
Moreover, in order to obtain some finite images, we factored the progenitor 2
∗
6
: C
3
o C
2
by the following relations
(bt)
k
, (btt
b
)
l
, (abt
c
t)
m
, (cbt)
n
Table 6.4: Some finite images of the Progenitor 2
∗
6
: C
3
o C
2
k l m n Index in G Order of G Shape of G
5 10 5 4 400 7200 (A
5
× A
5
) : 2
3 11 11 10 5280 95040 M
12
3 9 9 15 36000 648000 (A
5
× A
5
× A
5
) : 3
8 4 5 6 1600 28800 2
•
[(A
5
× A
5
) : 2
2
]
0 10 5 4 4800 86400 (4 × 3) : [(A
5
× A
5
) : 2]
3 10 5 0 840 15120 (A
7
× 3) : 2
15 0 5 4 1200 21600 [(A
5
× A
5
) : 3] : 2
Then, we tried to apply the Lemma to find more images. Let t = t
6
. By using MAGMA,
we find that t commute with b. Thus, the presentation for the progenitor 2
∗
6
: Z
3
o Z
2
is given by
< a, b, c, t|a
3
, b
3
, (a, b), c
2
, a
c
= b, b
c
= a, t
2
, (t, b) >

111
Now, we will utilize the lemma by taking the stabiliser of two elements and determining
the centraliser of those points. The lemma deals with elements that have a permutation
(6,1) by itself, do have either 1 or 6, or do not have either of them.
N ∩ ht
0
, t
1
i ≤ C
N
(N
01
).
N
(01)
= hei.
C
N
(N
01
) = h(4, 5, 6), (1, 2, 3), (1, 5)(2, 6)(3, 4)i.
So, the choice for writing product of 2t
i
’s in terms of elements of N are unrestricted.
By running the set of the centralizer, we find that there is an element that includes the
transposition (6,1) such as.
(1, 6)(2, 4)(3, 5) = bcb
−1
.
Thus, we have to apply the lemma as the following:
(bcb
−1
t)
k
= 1, where k is odd.
To find some finite images of the progenitor 2
∗
6
: C
3
o C
2
, we have to add more relations
and run them in the background of MAGMA to have some of interesting group.
< a, b, c, t|a
3
, b
3
, (a, b), c
2
, a
c
= b, b
c
= a, t
2
, (t, b), (bcb
−1
t)
k
= 1, (ca
−1
t)
l
, (btt
c
)
m
,
(ab
2
t
c
)
n
, (bac
b
t)
o
> .
Table 6.5: Some finite images of the Progenitor 2
∗
6
: C
3
o C
2
k l m n o Index in G Order of G Shape of G
0 10 4 3 10 280 5040 A
7
: 2
∼
=
S
7
0 10 4 6 10 560 10080 2 × (A
7
: 2)
∼
=
2 × S
7
0 10 12 3 10 840 15120 (3 × A
7
) : 2
0 11 11 3 11 5280 95040 M
12
0 8 6 4 8 42240 760320 4 • (M
12
: 2)
0 9 9 3 9 144000 2592000 (4 : [A
5
× A
5
× A
5
]) : 2
0 12 5 4 12 403200 7257600 2
2
•
A
10
Moreover, by factoring the progenitor with all of the first order relations that found
from the conjugacy classes of C
3
o C
2
, we obtain similer groups as shown in table 6.5
and the following homomorphic image

112
2
∗
6
:C
3
oC
2
[ab
−1
t
(cb)
−1
]
2
,[bct]
15
,[cb
−1
t]
15
∼
=
(3
2
× 5) : S
3
6.3 The Progenitor 2
∗
6
: Z
2
o S
3
Consider the wreath product of H by K, denoted by H o K, where
H = Z
2
and K = S
3
.
By applying the same process as shown in section 6.2, the presentation for 2
∗
6
: Z
2
o S
3
is
< a
2
, b
2
, c
2
, (a, b), (a, c), (b, c), d
3
, e
2
, a
d
= b, b
d
= c, c
d
= a, a
e
= b, b
e
= a, c
e
= c, t
2
,
(t, a), (t, c), (t, ed) >
, where
a = (34),b = (56),c = (12),d = (145)(236), and e = (36)(45).
In order to obtain homomorphic images, we factored the progenitor by suitable relators.
Hence,
G =
2
∗
6
: C
2
o S
3
[d
−1
ct]
5
, [d
2
ett
b
]
2
, [cbtt
e
]
5
∼
=
(4 × 2
5
) : A
5
G =
2
∗
6
: C
2
o S
3
(t, t
b
), (t, t
e
)
∼
=
2
6
: (2
3
: S
3
)
The homomorphic images that are listed in the table below were found by factoring the
progenitor 2
∗
6
: C
2
o S
3
by all of the following first order relations.
(abct)
k
, (ct)
l
, (ct
d
)
m
, (act)
n
, (act
d
)
o
, (et)
p
, (et
d
)
q
, (cet)
r
,
(cet
d
)
s
, (dt)
u
, (cedt)
v
, (cedt
d
)
w
, (acet)
x
, (acet
d
)
y
, (cdt)
z
Table 6.6: Some finite images of the Progenitor 2
∗
6
: C
2
o S
3
k l . . . x y z Index in G Order of G Shape of G
0 0 . . . 5 2 5 10 120 2 × A
5
0 0 . . . 4 4 6 32 1536 (4
2
× 2) • (2
3
: S
3
)
0 0 . . . 6 2 18 162 1944 (9
2
× 2) : ([2 × 3] : 2)
0 0 . . . 6 0 7 210 10080 2 × S
7
0 0 . . . 6 2 14 98 1176 (2 × 7
2
) : ([2 × 3] : 2)
0 0 . . . 5 4 20 10240 491520 2
12
• (2 × A
5
)
113
Chapter 7
Monomial Progenitor of P
∗
n
:
m
N
7.1 Preliminaries
Definition 7.1 (Representation of G). A representation of a finite group G is defined
by φ : G
Homo
−→ GL(n, F), where GL(n, F) is the group of n × n invertible matrices over
a finite field F.
Definition 7.2 (Characters). The character χ afforded by the representation ρ :
G → GL(n, F) is a function
χ : G → F, given by χ(g) = T r(gρ) ∀g ∈ G.
Definition 7.3 (Equivelent Represntation). Let ρ : G
homo
→ GL(n, F) and T ∈
GL(n, F). Then, T
−1
ρT is also a representation of G and T
−1
ρT and ρ are called
equivelent.
Definition 7.4 (Faithful Represntation). Let ρ : G
Rep
→ GL(n, F) and
kerρ = {g ∈ G|gρ = I
n
}. Then, ρ is faithful if kerρ = 1.
Definition 7.5 (Trivial Represntation). A repesentation ρ : G
Rep
→ GL(n, F) given
by gρ = T
n
is a trivial representation of G.
Facts:
1. χ(x) = χ(y) if x and y are conjugates.
2. Equivelent representation have the same character.

114
3. The number of irreducible character of G is equal to the number of the conjugacy
classes of G.
Character Table:
Think of a character table as the matrix
χ
(i)
α
. In a character table
1. Let X be the row vector
~
α
χ
(i)
α
and
¯
Y be the conjugate of the row vector
χ
(i)
α
.
If i 6= j, then the ordinary dot product X ·
¯
Y = 0.
2. Let X be the row vector
~
α
χ
(i)
α
Then, the ordinary dot product X ·
¯
χ
(i)
α
= |G|
Note 7.6. χ
(i)
α
= χ
α
(g), where g is an element of the conjugacy class C
α
.
Definition 7.7 (Trivial Character). The trivial character is the character χ of the
trivial representation, where χ : G → F given by χ(g) = 1 ∀g ∈ G.
Definition 7.8 (Monomial Matrix). A square matrix that has exactly one non-zero
entry in each row and each column.
Definition 7.9 (Monomial Representations). Let G be a group. A Monomial rep-
resentations is a map A : G
Homo
→ GL(n, F) which provided that A(x) and A(y) are
monomial matrices.
Definition 7.10 (Monomial Character). A character φ of G is monomial if φ is
induced by a linear character of a subgroup H (not necessarily proper) of G.
Definition 7.11 (Induced Character). Let H ≤ G and φ be a character of G. The
formula for induced character is
φ
G
α
=
n
~
α
X
z∈C
α
∩H
φ(z),
where
φ
G
α
is the value of φ
G
at each element of the class C
α
.
n = [G : H].
~
α
is the number of elements in the class C
α
of G.
Example 7.12. Let G = S
3
and H = A
3
≤ G. We want to show that φ
G
is a monomial
character.

115
Table 7.1: Character Table of G = S
3
Classes C
1
C
2
C
3
Order 1 2 3
#Elements 1 3 2
χ
1
1 1 1
χ
2
1 -1 1
χ
3
2 0 -1
Table 7.2: Character Table of H = A
3
Classes C
1
C
2
C
3
Order 1 3 3
#Elements 1 1 1
χ
1
1 1 1
χ
2
1 J − 1 −J
χ
3
1 −1 − J J
J = RootOfUnity(3)
G = S
3
= {(1), (12), (13), (23), (123), (132)}.
H = A
3
= {(1), (123), (132)}
∼
=
Z
3
.
The index of H in G is equal to n =
|S
3
|
|A
3
|
=
6
3
= 2
Since A
3
∼
=
Z
3
, the cube root of unity is J. Thus, 1 + J + J
2
= 0.
Now, we want to induce G by the second linear character φ = χ
(2)
of H.
φ
G
1
=
2
1
X
z∈C
1
∩H
φ(z) = 2 · φ(1) = 2(1) = 2.
φ
G
2
=
2
3
X
z∈C
2
∩H
φ(z) = 2 · φ(0) = 0.
φ
G
3
=
2
2
X
z∈C
3
∩H
φ(z) =
2
2
[φ((123)) + φ((132)) = J + J
2
= −1.
We see that
φ
G
1
= 2 = χ
(3)
1
, φ
G
2
= 0 = χ
(3)
2
, and φ
G
3
= −1 = χ
(3)
3
.
We show that φ
G
is a monomial Character.
To find a monomial representation of a finite group G, we have to know the
following:

116
1. The number of the linear character of G is equal to |G/
´
G|.
2. G/
´
G is an abelian group.
3. Assume G/
´
G
∼
=
Z
3
. Then, the linear characters have 3rd roots of unity as its
entries.
4. Character φ of the group G is irreducible ⇔ hφ, φi = 1, where
hφ, φi =
1
|G|
k
X
α=1
~
α
φ
α
¯
φ
α
.
5. All linear representations of a finite group G are monomial.
6. Let B be a linear representation of a proper subgroup H of G, and let
G =
S
n
i=1
Ht
i
. Then, a monomial representation of G is given by
A(x) =
B
t
1
xt
−1
1
· · · B
t
1
xt
−1
n
B
t
2
xt
−1
1
· · · B
t
2
xt
−1
n
.
.
. · · ·
.
.
.
B
t
n
xt
−1
1
· · · B
t
n
xt
−1
n
Example 7.13. Let G = S
3
= h(123), (12)i and H = A
3
= h(123)i. The character
table of G and H are given in Ex 7.11.
The transversal (right cosets) of G/H is {e, (12)}. Thus,
G = He ∪ H(12) = Ht
1
∪ Ht
2
.
Since J is the cube root of unity, J = 2 and J
2
= 4. The representitive of H are:
B(e) = e.
B((123)) = J − 1 = 1.
B((132)) = −J = −2.
117
The two monomial representations are
A(x) =
B(t
1
xt
−1
1
) B(t
1
xt
−1
2
)
B(t
2
xt
−1
1
) B(t
2
xt
−1
2
)
=
B(exe) B(ex(12))
B((12)xe) B((12)x(12))
=
B((123)) B((123)(12)) /∈ A
3
B((12)(123) /∈ A
3
B((12)(123)(12))
=
1 0
0 −2
A(y) =
B(t
1
yt
−1
1
) B(t
1
yt
−1
2
)
B(t
2
yt
−1
1
) B(t
2
yt
−1
2
)
=
B(eye) B(ey(12))
B((12)ye) B((12)y(12))
=
B((12)) /∈ A
3
B(e)
B(e) B((12)) /∈ A
3
=
0 1
1 0
Induced Characters:
Assume the following:
- G is a group of order q.
- H is a subgroup of G with index n in G.
- B is a representation of H of degree m.
By the latter assumption, there exist a map B : H
Homo
−→ GL(m, F) that is given by
B(uv) = B(u)B(v), ∀u, v ∈ H. We want to extend B to give a presentation of G. Thus,
define A : G → GL(, F) by
A(x) =
B(x), if x ∈ H
0, if x /∈ H.
.
Let x, y ∈ G.
A(xy) =
B(xy), if xy ∈ H
0, if xy /∈ H.
.
In this chapter, we are going to write monomial presentation for the monomial
progenitors of the form p
∗
n
:
m
N, where p ≥ 3 and N is isomorphic to 2
•
A
5
, L
2
(7), and
A
7
, and look for the homomorphic images of the progenitor, where N acts monomially
on the symmetric generators of order p. Thus, we need a subgroup H of N whose index
118
in G is equal to n.
Then, we will be able to form a monomial progenitor 3
∗
n
:
m
N. The next examples will
illustrate what we have written above.
7.2 Monomial Progenitor 3
∗
12
:
m
(2
•
A
5
)
Consider the group 3
∗
12
:
m
(2
•
A
5
), where G = 2
•
A
5
. By knowing the presen-
tation for G = 2
•
A
5
= ha, b|a
4
, b
3
, (ab)
5
, (a
2
, b)i, where
a ≈ (1, 2, 5, 4)(3, 6, 8, 7)(9, 13, 11, 14)(10, 15, 12, 16)(17, 19, 18, 20)(21, 24, 23, 22)
b ≈ (1, 3, 2)(4, 5, 8)(6, 9, 10)(7, 11, 12)(13, 16, 17)(14, 15, 18)(19, 21, 22)(20, 23, 24)
we can write a monomial permutation representation of G. To obtain this, we have to
choose a subgroup H, not necessarily proper, of 2
•
A
5
and induced it up by a linear
character of H. First, we chose H to be a central extinsion of cyclic group of order 2
by D
10
, but we figured out that the character table of 2
•
D
10
does not have a faithful
character. So, by looking at the character table of G, we see that G is not an abelian
group since its classes does not have a single element. Thus, not every irreducible
character of G is faithful. Then, we choose H to be a Dihedral group of order 10 since it
has the same index 12 as the order of the irreducible character of G and it has a faithful
character (not necessary irreducible).
To find the value of ω in the table 7.4, we have to determine the smallest finite
field that has square roots of unity. Since the non-zero entries of the two monomial
matrices are 1 and 2, we conclude that the smallest finite field is F
3
. If |F
3
| = 3, then
|F
∗
3
| = 2 is a cyclic group of order 2. So, F
3
= {0, 1, 2} consists a cyclic group of order
2. Since < 1 >= {1, 1
2
} = {1, 2}, we see that
2
2
= 4 ≡
3
1
So, the value for ω is equal to 2. Therefore, the value for the different powers of ω are
given by
ω
2
= ω · ω = 2 · 2 = 4 ≡
3
1
ω
3
= ω · ω
2
= 2 · 1 = 2
ω
4
= ω
2
· ω
2
= 1 · 1 = 1

119
Table 7.3: Character Table of G = 2
•
A
5
χ C
1
C
2
C
3
C
4
C
5
C
6
C
7
C
8
C
9
χ
1
1 1 1 1 1 1 1 1 1
χ
2
2 -2 -1 0 Z1 Z1#2 1 −Z1 −Z1#2
χ
3
2 -2 -1 0 Z1#2 Z1 1 −Z1#2 −Z1
χ
4
3 3 0 -1 −Z1#2 −Z1 0 −Z1#2 −Z1
χ
5
3 3 0 -1 −Z1 −Z1#2 0 −Z1 −Z1#2
χ
6
4 -4 1 0 -1 -1 -1 1 1
χ
7
4 4 1 0 -1 -1 1 -1 -1
χ
8
5 5 -1 1 0 0 -1 0 0
χ
9
6 -6 0 0 1 1 0 -1 -1
# denotes algebraic conjugation
Z
1
is the square root of unity
Table 7.4: Character Table of N = D
10
χ C
1
C
2
C
3
C
4
C
5
C
6
C
7
C
8
C
9
C
10
χ
1
1 1 1 1 1 1 1 1 1 1
χ
2
1 -1 1 1 1 1 -1 -1 -1 -1
χ
3
1 1 ω ω
2
ω
3
ω
4
ω ω
3
ω
2
ω
4
χ
4
1 -1 ω ω
2
ω
3
ω
4
-ω -ω
3
-ω
2
-ω
4
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
χ
10
1 -1 ω
4
ω
3
ω
2
ω -ω
4
-ω
2
-ω
3
-ω
Now, we want to induce H = D
10
up to G = 2
•
A
5
to find the two induced representations
A(a) and A(b) of degree
|G|
|N|
=
120
10
= 12 of G. Thus, we choose to induce the nonprinciple
linear character χ
2
of H. It gives the follwing character (12,-12,0,0,2,2,0,-2,-2). Since
we are dealing with 12 × 12 matrices, we run the following loop to find the non-zero
entries for the two monomial representations A(a) and A(b) that generated 2
•
A
5
.
A:=[0:i in [1..144]];
for i in [1..12] do if a
*
T[i]ˆ-1 in N then i,
chN[2](a
*
T[i]ˆ-1); end if; end for;
for i in [1..12] do if T[2]
*
a
*
T[i]ˆ-1 in N then i,
chN[2](T[2]
*
a
*
T[i]ˆ-1); end if; end for;
.
.
.
for i in [1..12] do if T[12]
*
a
*
T[i]ˆ-1 in N then i,
120
chN[2](T[12]
*
a
*
T[i]ˆ-1); end if; end for;
Thus, we obtain
A(a) =
0 1 0 0 0 0 0 0 0 0 0 0
−1 0 0 0 0 0 0 0 0 0 0 0
0 0 0 −1 0 0 0 0 0 0 0 0
0 0 1 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 0 0 0 −1 0
0 0 0 0 0 0 0 0 0 0 0 1
0 0 0 0 0 0 0 0 0 1 0 0
0 0 0 0 −1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 −1 0 0 0 0
0 0 0 0 0 1 0 0 0 0 0 0
0 0 0 0 0 0 −1 0 0 0 0 0
and
A(b) =
0 0 1 0 0 0 0 0 0 0 0 0
0 0 0 1 0 0 0 0 0 0 0 0
0 0 0 0 1 0 0 0 0 0 0 0
0 0 0 0 0 0 1 0 0 0 0 0
1 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 −1
0 1 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 1 0 0 0 0
0 0 0 0 0 −1 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 1 0
A(a) and A(b) are monomial matrices since there is one non-zero entry other than
1 in each row and column. By checking the order of the two matrices, we see that
|A(a)| = 4 = |a|, |A(b)| = 3 = |b|, and |A(a) ∗ A(b)| = 5 = |a ∗ b|. hA(a), A(b)i is a
faithful representation of 2
•
A
5
. Now, we want to write a permutation representation of

121
the two monomial matrices. Elements of the free product 3
∗
12
are of the form < t
1
>
∗ < t
2
> ∗ . . . ∗ < t
11
> ∗ < t
12
>, where |t
i
| = 3 and < t
i
>= {e, t
i
, t
i
2
} for ∀1 ≤ i ≤ 12.
To determine the permutaion representation of the monomial progenitor, we first find
Table 7.5: Labeling for t
i
’s
1 2 3 4 5 6 7 8 9 10 11 12
t
1
t
1
2
t
2
t
2
2
t
3
t
3
2
t
4
t
4
2
t
5
t
5
2
t
6
t
6
2
13 14 15 16 17 18 19 20 21 22 23 24
t
7
t
7
2
t
8
t
8
2
t
9
t
9
2
t
10
t
10
2
t
11
t
11
2
t
12
t
12
2
the permutation representation of G. Let x = A(a). We look at the non-zero entry of
A(a) a
i,j
such that
a
1,2
= 1 ⇒ the automorphism takes t
1
→ t
2
, so A(a) takes 1 to 3 in our labeling above.
Moreover, when t
1
2
→ t
2
2
, A(a) takes 2 to 4
a
2,1
= −1 ≡
3
2 ⇒ the automorphism takes t
2
→ t
1
2
,so A(a) takes 3 to 2.
Moreover, when t
2
2
→ t
1
, A(a) takes 4 to 1.
.
.
.
Table 7.6: Permutaion of x = A(a)
1 2 3 4 5 6 7 8 9 10 11 12
t
1
t
1
2
t
2
t
2
2
t
3
t
3
2
t
4
t
4
2
t
5
t
5
2
t
6
t
6
2
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
t
2
t
2
2
t
1
2
t
1
t
4
2
t
4
t
3
t
3
2
t
9
t
9
2
t
11
2
t
11
3 4 2 1 8 7 5 6 17 18 22 21
13 14 15 16 17 18 19 20 21 22 23 24
t
7
t
7
2
t
8
t
8
2
t
9
t
9
2
t
10
t
10
2
t
11
t
11
2
t
12
t
12
2
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
t
12
t
12
2
t
10
t
10
2
t
5
2
t
5
t
8
2
t
8
t
6
t
6
2
t
7
2
t
7
23 24 19 20 10 9 16 15 11 12 14 13
The permutaion of x is
(1,3,2,4)(5,8,6,7)(9,17,10,18)(11,22,12,21)(13,23,14,24)(15,19,16,20).
Similarly for the permutation of y = A(b).
The permutation for y is

122
Table 7.7: Permutaion of y = A(b)
1 2 3 4 5 6 7 8 9 10 11 12
t
1
t
1
2
t
2
t
2
2
t
3
t
3
2
t
4
t
4
2
t
5
t
5
2
t
6
t
6
2
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
t
3
t
3
2
t
4
t
4
2
t
5
t
5
2
t
7
t
7
2
t
1
t
1
2
t
12
2
t
12
5 6 7 8 9 10 13 14 1 2 24 23
13 14 15 16 17 18 19 20 21 22 23 24
t
7
t
7
2
t
8
t
8
2
t
9
t
9
2
t
10
t
10
2
t
11
t
11
2
t
12
t
12
2
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
t
2
t
2
2
t
9
t
9
2
t
10
t
10
2
t
8
t
8
2
t
2
6
t
6
t
11
t
11
2
3 4 17 18 19 20 15 16 12 11 21 22
(1,5,9)(2,6,10)(3,7,13)(4,8,14)(11,24,22)(12,23,21)(15,17,19)(16,18,20).
To write a presentation for the monoial progenitor 3
∗
12
:
m
(2
•
A
5
), let t ≈ t
1
. Then, we
have to determine what element of H normalise G. Thus, we are looking for t
1
such
that
g ∈ G 3 ht
1
i
g
= ht
1
i
{e, t
1
, t
2
1
}
g
= {e, t
1
, t
2
1
}
{t
1
, t
2
1
}
g
= {t
1
, t
2
1
}.
Either t → t
2
and t
2
→ t or t → t and t
2
→ t
2
. The normliser of the subgroup
< t
1
> is generated by
(5, 11, 24, 10, 19)(6, 12, 23, 9, 20)(7, 15, 17, 14, 21)(8, 16, 18, 13, 22), and
(1, 2)(3, 4)(5, 6)(7, 8)(9, 10)(11, 12)(13, 14)(15, 16)(17, 18)(19, 20)(21, 22)(23, 24)
Now, we must write these permutations in terms of x and y by using the Schreier System
for G, to make them commute with < t >.
(5, 11, 24, 10, 19)(6, 12, 23, 9, 20)(7, 15, 17, 14, 21)(8, 16, 18, 13, 22) = xyxy
−1
(1, 2)(3, 4)(5, 6)(7, 8)(9, 10)(11, 12)(13, 14)(15, 16)(17, 18)(19, 20)(21, 22)(23, 24) = x
2
Note that the first permutation fix t
1
, so it will have the following form (t, xyxy
−1
) or
t
xyxy
−
1
t
−1
. The second one sends t
1
→ t
2
, so t
2
1
→ t
2
2
. Therefore, we will write it in the

123
following form t
x
2
t
−2
.
Now, we can write the desired monomial presentation
3
∗
12
:
m
(2
•
A
5
) = hx, y, t|x
4
, y
3
, (xy)
5
, (x
2
, y), t
3
, (t, xyxy
−1
), t
x
2
t
−2
i.
To find some finite images, we add the following relations to the progenitor of 3
∗
12
:
m
(2
•
A
5
).
(x
2
yt
y
)
k
, (xyt)
l
, (xy
2
t
(
x
y
))
m
, (x
2
ytt
x
y
)
n
But, we could not find any homomorphic images except
G =
3
∗
12
:
m
(2
•
A
5
)
(t
1
,t
i
)
∼
=
3
12
: (2
•
A
5
), where i = 2, 3, 4, 5, 9, 7, 8.
The presentation for G is
hx, y, t|x
4
, y
3
, (xy)
5
, (x
2
, y), t
3
, (t, xyxy
−1
), t
x
2
t
−2
,
(t, t
x
2
), (t, t
x
), (t, t
x
3
), (t, t
y
), (t, t
y
2
), (t, t
xy
), (t, (t
xy
)
x
2
)i.
Now, we have to prove that 3
12
: (2
•
A
5
) is isomorphic to G. So, we need t
1
, t
2
, . . . , t
12
in terms of t
x
i
∗y
j
. We already knew that the presentation for 3
∗
12
:
m
(2
•
A
5
) is
hx, y, t
1
, t
2
, t
3
, t
4
, t
5
, t
6
, t
7
, t
8
, t
9
, t
10
, t
11
, t
12
|x
4
, y
3
, (xy)
5
, (x
2
, y), t
3
1
, t
3
2
, t
3
3
, t
3
4
, t
3
5
, t
3
6
, t
3
7
, t
3
8
,
t
3
9
, t
10
3
, t
11
3
, t
12
3
, t
x
1
=?, t
x
2
=?, . . . , t
12
x
=?, t
y
1
=?, t
y
2
=?, . . . , t
12
y
=?i.
We have shown that N = 2
•
A
5
= {x, y|x
4
, y
3
, (xy)
5
, (x
2
, y)}. Now, by using the gen-
erated of N and our labeling for t
0
i
s we need to find the action of N elements on the
elements of 3
12
. Since the permutation x takes 1 to 3, by our labeling we see that
t
x
1
= t
2
. Also, x takes 3 to 2. Thus, t
x
2
= t
2
1
and so on for the other t
0
i
s. Similarly, the
permutation y takes 1 to 5 and 5 to 9, thus t
y
1
= t
3
and t
y
3
= t
5
, respectively. We keep
doing the same process for the rest of t
0
i
s. Instead of writing t
1
, t
2
, . . . , t
12
, we will use
the following labeling
a
t
1
,
b
t
2
,
c
t
3
,
d
t
4
,
e
t
5
,
f
t
6
,
g
t
7
,
h
t
8
,
i
t
9
,
j
t
10
,
k
t
11
,
l
t
12

124
Thus, the monomial progenitor has the following symmetric presentation
H =<
3
12
z }| {
a, b, c, d, e, f, g, h, i, j, k, l,
N
z}|{
x, y |a
3
, b
3
, c
3
, d
3
, e
3
, f
3
, g
3
, h
3
, i
3
, j
3
, k
3
, l
3
, (a, b), (a, c),
(a, d), (a, e), (a, f), (a, g), (a, h), (a, i), (a, j), (a, k), (a, l), (b, c), (b, d), (b, e), (b, f ), (b, g),
(b, h), (b, i), (b, j), (b, k), (b, l), (c, d), (c, e), (c, f), (c, g), (c, h), (c, i), (c, j), (c, k), (c, l),
(d, e), (d, f ), (d, g), (d, h), (d, i), (d, j), (d, k), (d, l), (e, f), (e, g), (e, h), (e, i), (e, j), (e, k),
(e, l), (f, g), (f, h), (f, i), (f, j), (f, k), (f, l), (g, h), (g, i), (g, j), (g, k), (g, l), (h, i), (h, j),
(h, k), (h, l), (i, j), (i, k), (i, l), (j, k), (j, l), (k, l), x
4
, y
3
, (xy)
5
, (x
2
, y), a
x
= b, b
x
= a
2
,
c
x
= d
2
, d
x
= c, e
x
= i, f
x
= k
2
, g
x
= l, h
x
= j, i
x
= e
2
, j
x
= h
2
, k
x
= f, l
x
= g
2
, a
y
= c,
b
y
= d, c
y
= e, d
y
= g, e
y
= a, f
y
= l
2
, g
y
= b, h
y
= i, i
y
= j, j
y
= h, k
y
= f
2
, l
y
= k > .
To check, we run the following loop
> V:=CosetSpace(H,sub<H|w,z>: CosetLimit:=10000000, Hard:=true,
Print:=1);
#--- Run Parameters ---
Wo:280000056; Max:10000000; Mess:10000; Ti:-1; Ho:-1; Loop:0;
As:0; Path:0; Row:1; Mend:0; No:106; Look:0; Com:10;
C:1000; R:1; Fi:37; PMod:3; PSiz:256; DMod:4; DSiz:1000;
#---------------------------------
SG: a=1 r=1 h=1 n=2; l=1 c=+0.00; m=1 t=1
RS: a=91 r=1 h=1 n=92; l=2 c=+0.00; m=91 t=91
.
.
.
CP: a=530091 r=530 h=14362 n=530092; l=1061 c=+1.23;
m=530091 t=530091
INDEX = 531441 (a=531441 r=532 h=531442 n=531442;
l=1066 c=32.65; m=531441 t=531441)
> H:=CosetImage(V);
> CompositionFactors(H);
G
| Alternating(5)
*
| Cyclic(2)
*
| Cyclic(3)
*
| Cyclic(3)
*
125
| Cyclic(3)
*
| Cyclic(3)
*
| Cyclic(3)
*
| Cyclic(3)
*
| Cyclic(3)
*
| Cyclic(3)
*
| Cyclic(3)
*
| Cyclic(3)
*
| Cyclic(3)
*
| Cyclic(3)
1
So, the |H| = 3
12
× 120 = 531441 × 120 = 63772920.
7.3 Monomial Progenitor 3
∗
7
:
m
L
2
(7)
Consider
G = L
2
(7).
∼
=
h(2, 4)(3, 5), (1, 2, 3)(5, 6, 7)i.
∼
=
hx, y|x
2
, y
3
, (xy)
7
, (x, y)
4
i.
The MAGMA input for this group is as the following:
> G<x,y>:=Group<x,y|xˆ2,yˆ3,(x
*
y)ˆ7,(x,y)ˆ4>;
> S:=Sym(7);
> xx:=S!(2,4)(3,5);
> yy:=S!(1,2,3)(5,6,7);
> G1:=sub<S|xx,yy>;
> #G;
168
To find the monomial representations of L
2
(7), we need to find H ≤ L
2
(7) such that
[H :
´
H] = 2 for entries of the monomial representation to be in Z
3
.
126
> S:=Subgroups(G1);
> for i in [1..#S] do if Index(S[i]‘subgroup,
DerivedGroup(S[i]‘subgroup)) eq 2 then
Index(G1,S[i]‘subgroup), i; end if; end for;
84 2
28 8
7 13
7 14
> H:=S[13]‘subgroup;
> H;
Permutation group H acting on a set of cardinality 7
Order = 24 = 2ˆ3
*
3
(2, 7)(3, 6)
(1, 2, 4)(3, 6, 5)
(1, 2)(4, 7)
(1, 4)(2, 7)
> H:=sub<G1|(2, 7)(3, 6),(1, 2, 4)(3, 6, 5),
(1, 2)(4, 7),(1, 4)(2, 7)>;
> #H;
24
> dH:=DerivedGroup(H);
> f,g:=CosetAction(H,dH);
> #Generators(H);
4
> f(H.1), f(H.2),f(H.3), f(H.4);
(1, 2)
Id(g)
Id(g)
Id(g)
By running out all the four generators of H, we get three of them are the identities.
> C<u>:=CyclotomicField(2);
> M:=MatrixAlgebra(C,1);
> HM:=GModule(H,[M![u],M![1],M![1],M![1]]);
> I:=Induction(HM,G1);
> Norm(Character(I));
1
> GP:=MatrixGroup(I);
> #GP;
168
127
Now, we have to write down the monomial matrices φ(x) and φ(y). By using MAGMA,
we obtain the following two matrices
φ(x) =
−1 0 0 0 0 0 0
0 1 0 0 0 0 0
0 0 0 1 0 0 0
0 0 1 0 0 0 0
0 0 0 0 0 1 0
0 0 0 0 1 0 0
0 0 0 0 0 0 −1
φ(y) =
0 1 0 0 0 0 0
0 0 1 0 0 0 0
1 0 0 0 0 0 0
0 0 0 1 0 0 0
0 0 0 0 0 0 1
0 0 0 0 0 1 0
0 0 0 1 0 0 0
Now, we have to write the permutation representation of the irreduicable monomial
representation φ(x) and φ(y) of L
2
(7) by knowing four cases
• If a
ij
= 1, the automorphism takes t
i
→ t
j
.
• If a
ij
= −1, the automorphism takes t
i
→ t
−1
j
.
Where a
ij
is the non-zero entry in row i column j.
• If the automorphism takes t
i
→ t
j
, then t
−1
i
takes to t
−1
j
.
• If the automorphism takes t
i
→ t
−1
j
, then t
−1
i
takes to t
j
.

128
Table 7.8: The Permutation for A = φ(x)
1 2 3 4 5 6 7 8 9 10 11 12 13 14
t
1
t
2
t
3
t
4
t
5
t
6
t
7
t
−1
1
t
−1
2
t
−1
3
t
−1
4
t
−1
5
t
−1
6
t
−1
7
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
t
−1
1
t
2
t
4
t
3
t
6
t
5
t
−1
7
t
1
t
−1
2
t
−1
4
t
−1
3
t
−1
6
t
−1
5
t
7
8 2 4 3 6 5 14 1 9 11 10 13 12 7
Table 7.9: The Permutation for B = φ(y)
1 2 3 4 5 6 7 8 9 10 11 12 13 14
t
1
t
2
t
3
t
4
t
5
t
6
t
7
t
−1
1
t
−1
2
t
−1
3
t
−1
4
t
−1
5
t
−1
6
t
−1
7
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
t
2
t
3
t
1
t
5
t
7
t
6
t
4
t
−1
2
t
−1
3
t
−1
1
t
−1
5
t
−1
7
t
−1
6
t
−1
4
2 3 1 5 7 6 4 9 10 8 12 14 13 11
Thus, we obtain the two monoial representations
A = φ(x) = (18)(34)(56)(7, 14)(10, 11)(12, 13).
B = φ(y) = (123)(457)(8, 9, 10)(11, 12, 14).
To check these permutations, we store the two given matrices in MAGMA as mat1 and
mat2.
> mat1:=GP.1; mat2:=GP.2;
> A:=perm(7,2,mat1);
> B:=perm(7,2,mat2);
> A; B;
(1, 8)(3, 4)(5, 6)(7, 14)(10, 11)(12, 13)
(1, 2, 3)(4, 5, 7)(8, 9, 10)(11, 12, 14)
> G2:=sub<Sym(14)|A,B>;
> s,t:=IsIsomorphic(G1,G2);
> s;
true
Thus, we have find the irreduicable monomial representions of L
2
(7).
To write a presentation for the progenitor of L
2
(7), we must write a representation for
L
2
(7).
a:=G2.1;
Order(a);
b:=G2.2;
Order(b);
G2:=sub<G2|a,b>;
Order(a
*
b);
129
Order((a,b));
H<a,b>:=Group<a,b|aˆ2,bˆ3,(a
*
b)ˆ7,(a,b)ˆ4>;
> #H;
168
> f2,h2,k2:=CosetAction(H,sub<H|Id(H)>);
> CompositionFactors(h2);
G
| A(1, 7) = L(2, 7)
1
N:=G2;
Now, we have to find the normaliser of H in G such that N (H) = {g ∈ G|H
g
= H}.
So, we are looking for elements that normalise L
2
(7) and takes {7,14} to {7,14}, then
store them.
G22:=Stabiliser(G2,{7,14});
G22;
c:=G2!(1, 4, 10)(2, 5, 6)(3, 8, 11)(9, 12, 13);
d:=G2!(1, 8)(2, 9)(3, 13)(4, 12)(5, 11)(6, 10);
e:=G2!(1, 8)(3, 4)(5, 6)(7, 14)(10, 11)(12, 13);
> G22 eq sub<G2|c,d,e>;
true
After writting a presentation for L
2
(7), we write its Schreier system to convert the
normaliser of < t > which are c, d, and e in L
2
(7) in terms of A and B. Morover, we
see that
t
c
7
= t
(1,4,10)(2,5,6)(3,8,11)(9,12,13)
7
= t
7
.
t
d
7
= t
(1,8)(2,9)(3,13)(4,12)(5,11)(6,10)
7
= t
7
.
t
e
7
= t
(1,8)(3,4)(5,6)(7,14)(10,11)(12,13)
7
= t
14
.
The normliser of < t > in L
2
(7) are t
(yxy
−1
xyxyxy
−1
xy)
t
−1
, t
(yxy
−1
xyxy
−1
)
t
−1
, and t
x
=
t
−1
.
Thus, the presentation for the monomial progenitor is given by
3
∗
7
:
m
L
2
(7) = hx, y, t|x
2
, y
3
, (xy)
7
, (x, y)
4
, t
3
, t
(yxy
−1
xyxyxy
−1
xy)
t
−1
, t
(yxy
−1
xyxy
−1
)
t
−1
,
t
x
= t
−1
i.
Generated by

130
x ≈ (1, 8)(3, 4)(5, 6)(7, 14)(10, 11)(12, 13),
y ≈ (1, 2, 3)(4, 5, 7)(8, 9, 10)(11, 12, 14).
To find some homomorphic images, we factored out the progenitor by some relations
such as
(xyt)
k
, (xt
y
t
2
)
l
, (x
y
t)
m
, (y
2
(xy)
5
t)
n
, (xy
−1
t)
o
Then, we tabulated the results as shown in Table 7.10.
Table 7.10: Some Finite Images for 3
∗
7
:
m
L
2
(7)
k l m n o Index(G, sub < G|x, y >) Order of G Shape of G
0 0 0 0 4 15 2520 A
7
0 0 0 4 0 2187 367416 3
7
: L
2
(7)
7.3.1 A
7
as a Homomorphic Image of 3
∗
7
:
m
L
2
(7)
Consider the group
G = 3
∗
7
:
m
L
2
(7)
= hx, y, t|x
2
, y
3
, (xy)
7
, (x, y)
4
, t
3
, t
(yxy
−1
xyxyxy
−1
xy)
t
−1
, t
(yxy
−1
xyxy
−1
)
t
−1
, t
x
= t
−1
i,
factored by [xy
−1
t]
4
.
N = L
2
(7) = hx, yi = h(1, 8)(3, 4)(5, 6)(7, 14)(10, 11)(12, 13),
(1, 2, 3)(4, 5, 7)(8, 9, 10)(11, 12, 14)i,
and let t = t
7
→ t
0
. So, by expanding the relation, we get
xy
−1
t
4
= e
xy
−1
t
7
4
= e
(xy
−1
)
4
t
(xy
−1
)
3
7
t
(xy
−1
)
2
7
t
(xy
−1
)
7
t
7
= e
(1, 6, 10, 4, 14, 2, 5)(3, 11, 7, 9, 12, 8, 13)t
11
t
13
t
12
t
7
= e
(xy
−1
)
4
t
11
t
13
= t
7
t
12
t
11
t
13
= (xy
−1
)
−4
t
7
t
12
The MAGMA input for this group is as the following:

131
S:=Sym(14);
xx:=S!(1, 8)(3, 4)(5, 6)(7, 14)(10, 11)(12, 13);
yy:=S!(1, 2, 3)(4, 5, 7)(8, 9, 10)(11, 12, 14);
N:=sub<S|xx,yy>;
#N;
G<x,y,t>:=Group<x,y,t|xˆ2,yˆ3,(x
*
y)ˆ7,(x,y)ˆ4,tˆ3,
tˆ(y
*
x
*
yˆ-1
*
x
*
y
*
x
*
y
*
x
*
yˆ-1
*
x
*
y)
*
tˆ-1,
tˆ(y
*
x
*
yˆ-1
*
x
*
y
*
x
*
yˆ-1)
*
tˆ-1,tˆx=tˆ-1,(x
*
yˆ-1
*
t)ˆ4>;
f,G1,k:=CosetAction(G,sub<G|x,y>);
#G; #k;
ts:=[Id(G1): i in [1..14]];
ts[7]:=f(t);
ts[1]:=f(((tˆy)ˆx)ˆy);
ts[2]:=f((((tˆy)ˆx)ˆy)ˆy);
ts[3]:=f((tˆy)ˆx);
ts[4]:=f(tˆy);
ts[5]:=f((tˆy)ˆy);
ts[6]:=f(((tˆy)ˆy)ˆx);
ts[14]:=f(tˆx) ;
ts[8]:=f((((tˆx)ˆy)ˆx)ˆy);
ts[9]:=f(((((tˆx)ˆy)ˆx)ˆy)ˆy);
ts[10]:=f(((tˆx)ˆy)ˆx);
ts[11]:=f((tˆx)ˆy);
ts[12]:=f(((tˆx)ˆy)ˆy);
ts[13]:=f((((tˆx)ˆy)ˆy)ˆx);
We need to find the index of N in G. To obtain this, we need to express G as a union
of double cosets which is here G = N eN ∪ Nt
0
N.
By using MAGMA, we obtain that t
0
= t
7
= t
14
x
. Thus, t
0
= t
14
= t
0
t
0
= t
−1
0
.
The double coset enumeration:
• Consider [∗] which is the notation of N eN = N .
The number of right cosets in [∗] =
|N|
|N|
=
168
168
= 1.
The orbits of N on {0,1,2,3,4,5,6,8,9,10,11,12,13,14} are {0,1,2,3,4,5,6} and
{8,9,10,11,12,13,14}.
Pick a representitive from each orbit, say t
0
and t
14
, and determine the double
coset that contains each one.
Nt
0
∈ [0].
Nt
14
∈ [14].
Since, Nt
−1
0
= Nt
0
⇒ Nt
14
= Nt
0
, thus, we have 14 go to [0].

132
• Consider [0] which is the notation of N t
0
N.
N
0
= h(1, 5, 13)(2, 4, 3)(6, 8, 12)(9, 11, 10), (1, 11, 6)(2, 12, 10)(3, 9, 5)(4, 13, 8)i
= N
(0)
.
The number of right cosets in [0] =
|N|
|N
(0)
|
=
168
12
= 14.
The orbit of N on {0,1,2,3,4,5,6,8,9,10,11,12,13,14} are {0}, {14}, and
{1,2,3,4,5,6,8,9,10,11,12,13}.
Nt
0
t
0
= t
−1
0
∈ [0] (1 stays in [0]).
Nt
0
t
14
= Nt
0
t
−1
0
= N ∈ [∗] (1 symmetric generator goes back to the double coset
[∗]).
Nt
0
t
1
∈ [0] (12 symmetric generators stay in the double coset [0]).
Figure 7.1: Cayley Diagram for A
7
Over L
2
(7)
The isomorphic image of the monomial progenitor have proved by MAGMA.
> S:=Sym(14);
> xx:=S!(1, 8)(3, 4)(5, 6)(7, 14)(10, 11)(12, 13);
> yy:=S!(1, 2, 3)(4, 5, 7)(8, 9, 10)(11, 12, 14);
> N:=sub<S|xx,yy>;
> #N;
168
> G<x,y,t>:=Group<x,y,t|xˆ2,yˆ3,(x
*
y)ˆ7,(x,y)ˆ4,tˆ3,\
tˆ(y
*
x
*
yˆ-1
*
x
*
y
*
x
*
y
*
x
*
yˆ\
-1
*
x
*
y)
*
tˆ-1,tˆ(y
*
x
*
yˆ-1
*
x
*
y
*
x
*
yˆ-1)
*
tˆ-1,tˆx=tˆ-1,
(x
*
yˆ-1
*
t)ˆ4>;
> f,G1,k:=CosetAction(G,sub<G|x,y>);
> #G; #k;
2520
1

133
> CompositionFactors(G1);
G
| Alternating(7)
1
Hence,
G ≈
3
∗
14
:
m
L
2
(7)
[xy
−1
t]
4
=1
∼
=
A
7
7.3.2 3
7
: L
2
(7) as a Homomorphic Image of 3
∗
7
:
m
L
2
(7)
Consider the group
G = 3
∗
7
:
m
L
2
(7)
= hx, y, t|x
2
, y
3
, (xy)
7
, (x, y)
4
, t
3
, t
(yxy
−1
xyxyxy
−1
xy)
t
−1
, t
(yxy
−1
xyxy
−1
)
t
−1
, t
x
= t
−1
i,
factored by [y
2
(xy)
5
t]
4
.
N = L
2
(7) = hx, yi = h(1, 8)(3, 4)(5, 6)(7, 14)(10, 11)(12, 13),
(1, 2, 3)(4, 5, 7)(8, 9, 10)(11, 12, 14)i,
and let t = t
7
→ t
0
. So, by expanding the relation, we get
y
2
(xy)
5
t
4
= e
y
2
(xy)
5
t
7
4
= e
(y
2
(xy)
5
)
4
t
(y
2
(xy)
5
)
3
7
t
(y
2
(xy)
5
)
2
7
t
(y
2
(xy)
5
)
7
t
7
= e
t
9
¯
t
0
t
2
t
7
= e
t
9
t
14
= t
7
t
2
.
We need to find the index of N in G. To obtain this, we need to express G as a union
of double cosets.
By using MAGMA, we obtain that t
0
= t
7
= t
14
x
. Thus, t
0
= t
14
= t
0
t
0
= t
−1
0
.
The double coset enumeration:
• Consider [∗] which is the notation of N eN = N .
The number of right cosets in [∗] =
|N|
|N|
=
168
168
= 1.
The orbits of N on {0,1,2,3,4,5,6,8,9,10,11,12,13,14} are {0,1,2,3,4,5,6} and

134
{8,9,10,11,12,13,14}.
Pick a representitive from each orbit, say t
0
and t
14
, and determine the double
coset that contains each one.
Nt
0
∈ [0].
Nt
14
∈ [14].
Since, Nt
14
= N t
0
⇒ N t
−1
0
= N t
0
⇒ N t
14
∈ [0] (14 symmetric generators take
to the double coset [0]).
• Consider [0].
N
0
= h(1, 13, 5)(2, 3, 4)(6, 12, 8)(9, 10, 11), (1, 11, 6)(2, 12, 10)(3, 9, 5)(4, 13, 8)i
= N
(0)
.
The number of right cosets in [0] =
|N|
|N
(0)
|
=
168
12
= 14.
The orbits of N on {0,1,2,3,4,5,6,8,9,10,11,12,13,14} are {0}, {14}, and
{1,2,3,4,5,6,8,9,10,11,12,13}.
Nt
0
t
0
= t
−1
0
∈ [0] (1 stays in [0]).
Nt
0
t
14
= Nt
0
t
−1
0
= N ∈ [∗] (1 symmetric generator goes back to the double coset
[∗]).
Nt
0
t
1
∈ [0] (12 symmetric generators go to the double coset [01]).
• Consider [01].
N
01
= hei.
N
(0)
= h(1, 7)(3, 11)(4, 10)(5, 12)(6, 13)(8, 14)i.
The number of right cosets in [01] =
|N|
|N
(01)
|
=
168
2
= 84.
The orbits of N on {0,1,2,3,4,5,6,8,9,10,11,12,13,14} are {2}, {9}, {1,7}, {3,11},
{4,10}, {5,12}, {6,13}, and {8,14}.
Nt
0
t
1
t
1
= (Nt
0
t
1
)
(18)(29)(3,13)(4,12)(5,11)(6,10)
, so Nt
0
t
1
t
1
∈ [01] (2 stay)
Nt
0
t
1
t
2
∈ [012]
Nt
0
t
1
t
3
∈ [013]
Nt
0
t
1
t
4
∈ [014]
Nt
0
t
1
t
5
MAG
= (Nt
0
t
1
t
3
)
(1,5,4,13,2,3,7)(6,9,10,14,8,12,11)
, so Nt
0
t
1
t
5
∈ [013] (2 symmetric
generators go to the double coset [013])
Nt
0
t
1
t
6
MAG
= (Nt
0
t
1
t
3
)
(1,7,6,4,12,9,3)(2,10,8,14,13,11,5)
, so Nt
0
t
1
t
6
∈ [013] (2 symmetric

135
generators go to the double coset [013])
Nt
0
t
1
t
8
= Nt
0
t
1
t
−1
1
= Nt
0
, (2 symmetric generators go back to the double coset
[0])
Nt
0
t
1
t
9
∈ [019] (1 symmetric generator goes to the double coset [019]).
• Consider [012].
N
012
= hei
N
(012)
= h(2, 7)(3, 10)(4, 6)(5, 12)(9, 14)(11, 13), (1, 7)(3, 11)(4, 10)(5, 12)
(6, 13)(8, 14), (1, 7, 2)(3, 4, 13)(6, 10, 11)(8, 14, 9), (1, 2, 7)(3, 13, 4)
(6, 11, 10)(8, 9, 14), (1, 2)(3, 6)(4, 11)(5, 12)(8, 9)(10, 13)i.
The number of right cosets in [012] =
|N|
|N
(012)
|
=
168
6
= 28.
The orbits of N on {0,1,2,3,4,5,6,8,9,10,11,12,13,14} are {5,12}, {1,7,2}, {8,14,9},
and {3,4,6,10,11,13}.
Nt
0
t
1
t
2
t
2
MAG
= Nt
0
t
1
t
9
(3 symmetric generators take to the double coset [019]).
Nt
0
t
1
t
2
t
5
∈ [0125].
Nt
0
t
1
t
2
t
9
= Nt
0
t
1
t
2
t
−1
2
= Nt
0
t
1
(3 symmetric generators go back to the double
coset [01]).
Nt
0
t
1
t
2
t
3
∈ [0123].
• Consider [013].
N
013
= hei = N
(013)
.
The number of right cosets in [013] =
|N|
|N
(013)
|
=
168
1
= 168.
The orbits of N on {0,1,2,3,4,5,6,8,9,10,11,12,13,14} are {0}, {1}, {2}, {3}, {4},
{5}, {6}, {8}, {9}, {10}, {11}, {12}, {13} and {14}.
Nt
0
t
1
t
3
t
0
MAG
= (Nt
0
t
1
t
3
)
(13)(26)(4,11)(7,14)(8,10)(93)
(1 symmetric generator stays in the double coset [013]).
Nt
0
t
1
t
3
t
1
MAG
= (Nt
0
t
1
t
3
)
(18)(2,12)(3,7)(4,11(59)(10,14
(1 symmetric generator stays in the double coset [013]).
Nt
0
t
1
t
3
t
2
= Nt
0
t
1
t
2
t
3
(1 symmetric generator goes to the double coset [0123]).
Nt
0
t
1
t
3
t
3
MAG
= (Nt
0
t
1
t
4
)
(17)(3,1)(4,10)(5,12)(6,13)(8,14)
(1 symmetric generator takes to the double coset [014]).
Nt
0
t
1
t
3
t
4
∈ [0134] (1 symmetric generator goes to the double coset [0134]).

136
Nt
0
t
1
t
3
t
5
MAG
= (Nt
0
t
1
t
2
t
3
)
(1,5,4,13,2,3,7)(6,9,10,14,8,12,11)
(1 symmetric generator goes to the double coset [0123]).
Nt
0
t
1
t
3
t
6
∈ [0136] (1 symmetric generator goes to the double coset [0136]).
Nt
0
t
1
t
3
t
8
MAG
= (Nt
0
t
1
)
(1,7,3,2,13,4,5)(6,11,12,8,14,10,9)
(1 symmetric generator goes back to the double coset [01]).
Nt
0
t
1
t
3
t
9
MAG
= (Nt
0
t
1
t
3
t
6
)
(1,3,,12,4,6,7)(2,5,11,13,14,8,10)
(3 symmetric generators go to the double coset [019]).
Nt
0
t
1
t
3
t
1
0 = Nt
0
t
1
t
3
t
−1
3
= Nt
0
t
1
(1 symmetric generator goes back to the double coset [01]).
Nt
0
t
1
t
3
t
1
1 ∈ [01311] (1 symmetric generator goes to the double coset [01311]).
Nt
0
t
1
t
3
t
1
3
MAG
= (Nt
0
t
1
t
2
t
5
)
(135)(2,7,13)(6,9,14)(8,10,12)
(1 symmetric generator goes to the double coset [0125]).
Nt
0
t
1
t
3
t
1
4
MAG
= (Nt
0
t
1
)
(1,3,9,12,4,6,7)(2,5,11,13,14,8,10)
(1 symmetric generator goes back to the double coset [01]).
• Consider [014].
N
014
= hei.
N
(014)
= h(1, 7, 4)(2, 5, 13)(6, 9, 12)(8, 14, 11), (1, 4, 7)(2, 13, 5)(6, 12, 9)(8, 11, 14)i.
The number of right cosets in [014] =
|N|
|N
(014)
|
=
168
3
= 56.
The orbits of N on {0,1,2,3,4,5,6,8,9,10,11,12,13,14} are {3}, {10},
{0,1,4}, {2,5,13}, {6,9,12}, and {8,14,11}.
Nt
0
t
1
t
4
t
3
MAG
= Nt
0
t
1
t
3
t
4
(1 symmetric generator goes to the double coset [0134]).
Nt
0
t
1
t
4
t
4
MAG
= (Nt
0
t
1
t
3
)
(17)(3,11)(4,10)(5,12)(6,13)(8,14)
(3 symmetric generators go to
the double coset [013]).
Nt
0
t
1
t
4
t
10
∈ [01410] (1 symmetric generator takes to the double coset [01410]).
Nt
0
t
1
t
4
t
2
MAG
= (Nt
0
t
1
t
2
t
3
)
(172)(3,4,13)(6,10,11)(8,14,9)
(3 symmetric generators go to
the double coset [0142]).
Nt
0
t
1
t
4
t
6
MAG
= (Nt
0
t
1
t
3
t
6
)
(1,7,6,4,12,9,3)(2,10,8,14,13,11,5)
(3 symmetric generators go
to the double coset [0136]).
Nt
0
t
1
t
4
t
11
= Nt
0
t
1
t
4
t
−1
4
= Nt
0
t
1
(3 symmetric generators go back to the double
coset [01]).
• Consider [019].

137
N
019
= hei.
N
(019)
= h(2, 14)(3, 5)(4, 11)(6, 13)(7, 9)(10, 12), (1, 7)(3, 11)(4, 10)(5, 12)(6, 13)
(8, 14), (1, 7, 9)(2, 8, 14)(3, 12, 4)(5, 11, 10), (1, 9, 7)(2, 14, 8)(3, 4, 12)
(5, 10, 11), (1, 9)(2, 8)(3, 10)(4, 5)(6, 13)(11, 12)i
The number of right cosets in [019] =
|N|
|N
(019)
|
=
168
6
= 28.
The orbits of N on {0,1,2,3,4,5,6,8,9,10,11,12,13,14} are {6,13}, {1,7,9},
{2,14,8},and {3,5,11,12,4,10}.
Nt
0
t
1
t
9
t
2
= Nt
0
t
1
t
9
t
−1
9
= Nt
0
t
1
(3 symmetric generator go back to the double
coset [01]).
Nt
0
t
1
t
9
t
3
MAG
= (Nt
0
t
1
t
3
t
6
)
(1,3,9,12,4,6,7)(2,5,11,13,14,8,10)
(6 symmetric generators go
to the double coset [0136]).
Nt
0
t
1
t
9
t
6
MAG
= (Nt
0
t
1
t
3
¯
t
5
)
(1,7,6,4,12,9,3)(2,10,8,14,13,11,5)
(3 symmetric generators go
back to the double coset [013
¯
5]).
Nt
0
t
1
t
9
t
9
= Nt
0
t
1
t
2
(3 symmetric generators go to the double coset [012]).
We now continue the double coset enumeration by proceding in this manner
until the set of right cosets is closed under right multiplication by t
0
i
s where i = 0, · · · , 14
. Thus, we can determine the index of N in G. We conclude that
|G| ≤ (|N| +
|N|
|N
(0)
|
+
|N|
|N
(01)
|
+
|N|
|N
(012)
|
+ . . . +
|N|
|N
(012534
¯
6)
|
+
|N|
|N
(01346
¯
2
¯
5)
|
) × |N|
|G| ≤ (1 + 14 + 84 + 28 + 168 + 56 + 28 + 168 + 56 + 56 + 168 + 42 + 56 + 14+
84 + 84 + 168 + 168 + 168 + 168 + 168 + 56 + 56 + 56 + 56 + 8 + 8) × 168
|G| ≤ (2187 × 168) = 367416.
By considering the action of G on the 2187 cosets of L
2
(7) in G, we can show that
|G| ≥ 367416.

138
Figure 7.2: Cayley Diagram for 3
7
: L
2
(7) Over L
2
(7)
We now show that G
∼
=
3
7
: L
2
(7). The composition series is
G ⊇ G
1
⊇ G
2
⊇ G
3
⊇ G
4
⊇ G
5
⊇ G
6
⊇ G
7
⊇ 1,
where
G = (G/G
1
)(G
1
/G
2
)(G
2
/G
3
)(G
3
/G
4
)(G
4
/G
5
)(G
5
/G
6
)(G
6
/G
7
)(G
7
/1)
= L
2
(7)C
3
C
3
C
3
C
3
C
3
C
3
C
3
.
We want to determine the isomorphism type of the group G.
Normal subgroup lattice
-----------------------
[3] Order 367416 Length 1 Maximal Subgroups: 2
---
[2] Order 2187 Length 1 Maximal Subgroups: 1
---
[1] Order 1 Length 1 Maximal Subgroups:
139
> MinimalNormalSubgroups(G1);
[
Permutation group acting on a set of cardinality 2187
Order = 2187 = 3ˆ7
]
We note that the center of G is of order 1. So, this is not a central extension. Since
the minimal normal subgroups is an abelian p-group, we see that it is of order 2187.
Thus,|[2]| = 3
7
. By looking at the normal lattice of G, we see that it does not have
a normal subgroup of order 3. Thus, this is not a direct product of [2] by [3]. Now,
we want to check if it is a semi-direct product of [2] by L
2
(7). We find that it is by
investigating the derived group of G.
> DD:=DerivedGroup(G1);
> DD;
Permutation group G1 acting on a set of cardinality 2187
Order = 367416 = 2ˆ3
*
3ˆ8
*
7
Since the order of the derived group is equal to the order of [3] which is the whole group
G, G is a perfect group. So, we can write a presentation for G by using the perfect
group database.
> DB:=PerfectGroupDatabase();
> PermutationGroup(DB,367416,1);
Permutation group acting on a set of cardinality 2187
> s:=IsIsomorphic(PermutationGroup(DB,367416,1),G1);
> s;
false
> PermutationGroup(DB,367416,2);
> s:=IsIsomorphic(PermutationGroup(DB,367416,2),G1);
> s;
true
> Group(DB,367416,2);
Since the first presentation is not isomorphic to [3], we chose the second one which it
is. We highligt the relation between the generators of 3
7
and L
2
(7). Thus, we were
able to write a presentation for 3
7
: L
2
(7). At the end, we check if this presentation is
isomorphic with G.
> H<a,b,t,u,v,x,y,w,z>:=Group<a,b,t,u,v,x,y,w,z|aˆ2,bˆ3,

140
(a
*
b)ˆ7,(a,b)ˆ4,tˆ3,uˆ3,vˆ3,xˆ3,yˆ3,wˆ3,zˆ3,(a,tˆ-1),
(t,u),(t,v),(t,w),(t,x),(t,y),(t,z),(u,v),(u,w),(u,x),
(u,y),(u,z),(v,w),(v,x),(v,y),(v,z),(w,x),(w,y),(w,z),
(x,y),(x,z),(y,z),(a,tˆ-1),aˆ-1
*
u
*
a
*
wˆ-1,aˆ-1
*
v
*
a
*
v,
aˆ-1
*
w
*
a
*
uˆ-1,aˆ-1
*
x
*
a
*
zˆ-1,aˆ-1
*
y
*
a
*
y,aˆ-1
*
z
*
a
*
xˆ-1,
bˆ-1
*
t
*
b
*
uˆ-1,bˆ-1
*
u
*
b
*
vˆ-1,bˆ-1
*
v
*
b
*
tˆ-1,
bˆ-1
*
w
*
b
*
xˆ-1,bˆ-1
*
x
*
b
*
yˆ-1,bˆ-1
*
y
*
b
*
wˆ-1,(b,zˆ-1)>;
> f,H1,k:=CosetAction(H,sub<H|Id(H)>);
> #H;
367416
> s:=IsIsomorphic(H1,G1);
> s;
true
So, we obtained that G
∼
=
3
7
: L
2
(7).
G ≈
3
∗
7
:
m
L
2
(7)
[y
2
(xy)
5
t]
4
=1
∼
=
3
7
: L
2
(7)
7.4 Monomial Progenitor 3
∗
21
:
m
A
7
Consider
G = A
7
.
∼
=
h(123), (34567)i.
∼
=
hx, y|x
3
, y
5
, (xy)
7
, (xx
y
)
2
, (xy
−2
xy
2
)
2
i.
By applying the same process as in section 3 and by using MAGMA, we were able to
find the following monomial progenitor 3
∗
21
:
m
A
7
hx, y, t|x
3
, y
5
, (xy)
7
, (xx
y
)
2
, (xy
−2
xy
2
)
2
, t
21
, t
y
= t, t
(xyx
−1
yxy
−2
x
−1
)
t
−1
, t
(xyx
−1
y
−1
x)
ti
generated by
x ≈(1, 2, 4)(5, 7, 10)(8, 11, 15)(12, 16, 13)(17, 21, 41)(20, 38, 42)(22, 23, 25)
(26, 28, 31)(29, 32, 36)(33, 37, 34),
y ≈(1, 3, 6, 9, 13)(2, 5, 8, 33, 17)(4, 7, 11, 37, 20)(10, 14, 18, 36, 19)(12, 38, 23, 26, 29)
(15, 40, 31, 35, 39)(16, 41, 25, 28, 32)(22, 24, 27, 30, 34).

141
We factored the progenitor by the following relators
(x
2
t)
k
, (xyt
2
)
l
, (xx
y
t)
m
, (x
y
t
2
)
n
, (y
−2
xy
2
t)
o
, (y
−2
xt)
p
, (x
2
y
3
t
2
)
q
and we obtained that
G =
3
∗
21
:
m
A
7
[y
−2
xy
2
t]
2
, [y
−2
xt]
6
∼
=
A
8
The following computer-based proof gives that G
∼
=
A
8
.
> G<x,y,t>:=Group<x,y,t|xˆ3,yˆ5,(x
*
y)ˆ7,(x
*
xˆy)ˆ2,
(x
*
yˆ-2
*
x
*
yˆ2)ˆ2,tˆ3,tˆy=t,
tˆ(x
*
y
*
xˆ-1
*
y
*
x
*
yˆ-2
*
xˆ-1)
*
tˆ-1,tˆ(x
*
y
*
xˆ-1
*
yˆ-1
*
x)
*
t,
(yˆ-2
*
x
*
yˆ2
*
t)ˆ2,(yˆ-2
*
x
*
t)ˆ6,>;
> f,G1,k:=CosetAction(G,sub<G|x,y>);
> CompositionFactors(G1);
G
| Alternating(8)
1
> #sub<G|x,y>;
2520
> #DoubleCosets(G,sub<G|x,y>,sub<G|x,y>);
2
142
Chapter 8
Covering Group
In this chapter, we want to discover the relation between the central extension
and covering group, and how it leads to Schur multiplier.
Definition 8.1 (Central Extension). A central extension of a group G is defined to
be a group H such that there exist a homomorphism ρ from H onto G with Kerρ ≤ Z(H),
the center of H.
Definition 8.2 (Universal Central Extension). A central extension of H is said to
be a universal extension of G provided that if K is another central extension of G
then there exists a homomorphism φ from H onto K. In other words H is called the
universal cover group of G.
H/Kerφ
∼
=
K
The above definitions showed that a finite group G has a universal central
extension if and only if G is perfect.
Note 8.3. G is perfect if
´
G = G.
Example 8.4. 6
•
A
6
is a universal covering group of A
6
and 3
•
A
6
is a covering group
of A
6
.
Let H = 6
•
A
6
and K = 3
•
A
6
. We want to prove that there is a homomorphism
φ : 6
•
A
6
−→ 3
•
A
6
, such that 6
•
A
6
/Kerφ
∼
=
3
•
A
6
By using MAGMA, we obtain the following
143
> S:=Sym(432);
> a:=S!(1,2,8,5)...(427,430,428,429);
> b:=S!(1,3,14,12,8,22,21,6)...(395,421,431,424,396,\
> 423,432,422);
> G:=sub<S|a,b>;
> C:=Center(G);C;
> Order(C.1);
2
> Order(C.2);
6
> Order(C.2ˆ3);
2
> c:=C.2;
> Order(cˆ3);
2
Thus, we chose to factor H by the center < c
3
> of H of order 2 where
c = Z(H) = (1, 7, 9, 8, 18, 4) . . . (425, 428, 432, 426, 427, 431) = C.2.
c
3
= (1, 8)(2, 5) . . . (429, 430)(431, 432).
So, the composition for the factored group q is
> q,ff:=quo<G|cˆ3>;
> CompositionFactors(q);
G
| Alternating(6)
*
| Cyclic(3)
1
Now, we have to show that it is isomorphic to 3
•
A
6
which is generated by
(2, 6)(4, 11)(7, 9)(8, 13)(10, 14)(12, 16), and
(1, 2, 7, 4)(3, 8, 6, 10)(5, 9, 13, 12)(11, 15)(14, 17)(16, 18)
> S:=Sym(18);
> a:=S!(2,6)(4,11)(7,9)(8,13)(10,14)(12,16);
> b:=S!(1,2,7,4)(3,8,6,10)(5,9,13,12)(11,15)(14,17)(16,18);
> G1:=sub<S|a,b>;
> s:=IsIsomorphic(q,G1);
> s;
true
144
Thus, we have shown that there exist a homomorphism φ such that 6
•
A
6
/Kerφ
∼
=
3
•
A
6
.
Next, we want to exist a homomorphism
ρ : 3
•
A
6
−→ A
6
, such that 3
•
A
6
/Kerρ
∼
=
A
6
So, we have to factor q by the center of G1 which is
D = Z(G1) = (1, 5, 3)(2, 9, 8)(4, 12, 10)(6, 7, 13)(11, 16, 14)(15, 18, 17)
and check if it is isomorphic to A
6
.
> qq,fff:=quo<G1|D>;
> s:=IsIsomorphic(qq,Alt(6));
> s;
true
Hence, 6
•
A
6
is a universal covering group of A
6
.
Similarelly, we can prove that 6
•
A
6
is a universal covering group of A
6
and 2
•
A
6
is a
covering group of A
6
.
Definition 8.5 (Schur Multiplier). A Schur Multiplier of a group G, dnoted by
M(G), is the Kernal of the homomorphism ρ from
´
G onto G.
Note 8.6. Every simple group is Schur multiplier.
Note 8.7. The second homology group is known as the Schur multiplier.
Depending to the transposition of S
n
, we can extend 2
•
A
n
to 2
•
S
±
n
. Thus,
2
•
A
n
extends to 2
•
S
+
n
if the transposition lift to elements of order 2, and 2
•
A
n
extends
to 2
•
S
−
n
if the transposition lift to elements of order 4.
Now, we will state some facts about the Schur multiplier:
1. If G is a finite group, then the Schur multiplier M(G) is a finite abelian group.
2. The Schur multiplier M(G) is trivial if all the Sylow p-subgroups of G are cyclic.
Thus, the |M(G)| is not divisible by p, for some prime p.
Example 8.8. Let G be the nonabelian group, where |G| = 6 = 3 · 2. The Sylow
3-subgroup and Sylow 2-subgroup are cyclic. Thus, M(G) is trivial.
3. The Schur multiplier M (G) is trivial if G is the Quaternion group.
145
4. |M(G)| = 2 if G is the Dihedral groups.
5. The order of the Schur multiplier M(G) can be larger than the order of G.
Example 8.9. Let G be an elementry abelian group of order 16. The |M(G)| =
64.
In the next chapter, we will write more permutation and monoial progenitors
when N is a central extension.
146
Chapter 9
More Progenitors
9.1 2
•
A
5
Consider the group N = 2
•
A
5
= hx, y|x
4
, y
3
, (xy)
5
, (x
2
, y)i, where
x ≈ (1, 2, 5, 4)(3, 6, 8, 7)(9, 13, 11, 14)(10, 15, 12, 16)(17, 19, 18, 20)(21, 24, 23, 22)
y ≈ (1, 3, 2)(4, 5, 8)(6, 9, 10)(7, 11, 12)(13, 16, 17)(14, 15, 18)(19, 21, 22)(20, 23, 24)
9.1.1 The involutory Progenitor 2
∗
24
: (2
•
A
5
)
To write a presentation for this type of progenitor, we must introduce a new
variable t = t
1
of order 2, and find all elements of N that stabilise 1. By using MAGMA,
we obtain the following
(2, 8, 11, 15, 7)(3, 9, 16, 6, 4)(10, 18, 23, 19, 14)(12, 17, 21, 20, 13) = xy
Since t commutes with each generator of the one point stabiliser, we have to insert t
and with which commutes into our progenitor. Then, the presentation for 2
∗
24
: (2
•
A
5
)
is
hx, y, t|x
4
, y
3
, (xy)
5
, (x
2
, y), t
2
, (t, xy)i.
In order to search for relations, we use the following two methods
• Factor the progenitor by all of the first order relations.
By using MAGMA, we obtain a list of the conjugacy classes of N = 2
•
A
5
.

147
Table 9.1: Conjugacy Classes of N = 2
•
A
5
Class Representitive of the Class Elements of form πt
i
2 x
2
x
2
t
1
3 y yt
1
, yt
9
, yt
17
, yt
21
4 x xt
1
, xt
3
, xt
9
, xt
10
, xt
17
, xt
21
5 yx yxt
1
, yxt
2
, yxt
9
, yxt
21
6 (yx)
2
(yx)
2
t
1
, (yx)
2
t
2
, (yx)
2
t
9
, (yx)
2
t
21
7 yxyxy
−1
yxyxy
−1
t
i
,i = 1, 2, 9, 21
8 yx
−1
yx
−1
t
1
, yx
−1
t
2
, yx
−1
t
9
, yx
−1
t
21
9 xy
−1
x
−1
y
−1
xy
−1
x
−1
y
−1
t
i
, i = 1, 2, 9, 21
Since t ≈ t
1
, we get
t
2
= t
x
, t
3
= t
y
, t
9
= t
yxy
t
10
= t
yxy
−1
, t
17
= t
(xyxy
−1
)
2
, t
21
= t
(xy
−
1xy)
2
• Apply the Lemma.
We will utilize the lemma by taking the stabiliser of two elements and determining
the centraliser of those points. The lemma deals with elements that have the
transposition (1,2), do have either 1 or 2, or do not have either of them.
N ∩ ht
0
, t
1
i ≤ C
N
(N
01
).
N
(01)
= hei ⇒ C
N
(N
01
).
So, the choices for writing product of 2t
i
’s in terms of elements of N are unre-
stricted. By running the Set(C), we find that it does not have an element that
includes the transposition (1,2).

148
By adding all the relations from the above table and write some supporting relations,
the presentation for this progenitor is
< x, y, t|x
4
, y
3
, (xy)
5
, (x
2
, y), t
2
, (t, xy), (x
2
t)
k
, (yt
yxy
)
l
, (yt)
m
, (yt
(xyxy
−1
)
2
)
n
,
(yt
(xy
−1
xy)
2
)
o
, (xt)
p
, (xt
yxy
)
q
, (xt
(xy
−1
xy)
2
)
r
, (xt
y
)
s
, (xt
(xyxy
−1
)
2
)
dd
, (xt
yxy
−1
)
u
,
(yxt
(xy
−1
xy)
2
)
v
, (yxt
x
)
w
, (yxt)
a
, (yxt
yxy
)
b
, ((yx)
2
t
x
)
c
, ((yx)
2
t)
d
, ((yx)
2
t
(xy
−1
xy)
2
)
e
,
((yx)
2
t
yxy
)
i
, (yxyxy
−1
t)
j
, (yxyxy
−1
t
yxy
)
z
, (yxyxy
−1
t
x
)
g
, (yxyxy
−1
t
(xy
−1
xy)
2
)
h
,
(yx
−1
t
yxy
)
ee
, (yx
−1
t
x
)
rr
, (yx
−1
t)
mm
, (yx
−1
t
(xy
−1
xy)
2
)
zz
, (xy
−1
x
−1
y
−1
t
x
)
ww
,
(xy
−1
x
−1
y
−1
t)
pp
, (xy
−1
x
−1
y
−1
t
yxy
)
qq
, (xy
−1
x
−1
y
−1
t
(xy
−1
xy)
2
)
ss
, (xyt
y
t)
vv
, (xtt
x
)
uu
,
(yt
x
t
y
)
hh
, (xtt
x
t
y
)
ii
, (xt)
jj
, (yt)
kk
, (xyt
x
)
ll
> .
By running the progenitors 2
∗
24
: (2
•
A
5
) in the background of MAGMA, we obtain
some interesting group.
Table 9.2: Some finite images of the progenitor 2
∗
24
: (2
•
A
5
)
k · · · ii jj kk ll Index in G Order of G Shape of G
0 · · · 0 4 6 6 260 15600 L
2
(25) : 2
0 · · · 0 5 7 6 1050 126000 U
3
(5)
0 · · · 0 6 4 10 240 14400 2 • [(A
5
× A
5
) : 2]
0 · · · 0 8 0 4 25920 1555200 (2 × 3) • [(A
6
× A
6
) : 2]
0 · · · 0 8 4 8 2100 252000 2 × U
3
(5)
9.1.2 The Progenitor 3
∗
24
: (2
•
A
5
)
A presentation for the progenitor of 3
∗
24
: (2
•
A
5
), is
hx, y, t|x
4
, y
3
, (xy)
5
, (x
2
, y), t
3
, (t, xy)i.
We were able to find the images given in Table 8.3 by factoring this progenitor by the
following relators
(x
2
t)
k
, (yt
yxy
)
l
, (xt
yxy
−1
)
m
, (yxt
(xy
−1
xy)
2
)
n
, ((yx)
2
t
x
)
o
, (yxyxy
−1
t)
p
, (yx
−1
t
yxy
)
q
,
(xy
−1
x
−1
y
−1
t
x
)
r
, (xyt
y
t)
s
, (xtt
x
)
u
, (yt
x
t
y
)
v
, (xtt
x
t
y
)
w
, (xt)
i
, (yt)
j
, (xyt
x
)
f

149
Table 9.3: Some finite images of the progenitor 3
∗
24
: 2
•
A
5
k l · · · w i j f Index in G Order of G Shape of G
0 0 · · · 0 0 3 15 3 360 (2 × 3)•A
5
0 0 · · · 0 6 3 15 3 180 A
5
× 3
9.2 2
•
A
6
Consider the group N = 2
•
A
6
= hx, y|x
4
, y
8
, (xy)
5
, (xy
2
)
5
, (y
4
, x), (x
2
, y)i,
where
x ≈(1, 2, 4, 5)(3, 9, 11, 12)(6, 16, 13, 17)(7, 19, 14, 21)(8, 22, 15, 23)(10, 27, 18, 28)
(20, 35, 24, 36)(25, 41, 29, 42)(26, 43, 30, 44)(31, 49, 33, 51)(32, 52, 34, 53)
(37, 59, 39, 61)(38, 62, 40, 63)(45, 69, 47, 71)(46, 58, 48, 56)(50, 64, 54, 60)
(55, 77, 57, 78)(65, 68, 66, 67)(70, 76, 72, 74)(73, 80, 75, 79).
y ≈(1, 3, 10, 13, 4, 11, 18, 6)(2, 7, 20, 15, 5, 14, 24, 8)(9, 25, 19, 30, 12, 29, 21, 26)
(16, 31, 50, 34, 17, 33, 54, 32)(22, 37, 60, 40, 23, 39, 64, 38)(27, 45, 70, 48, 28, 47, 72, 46)
(35, 55, 79, 58, 36, 57, 80, 56)(41, 63, 69, 66, 42, 62, 71, 65)(43, 53, 78, 68, 44, 52, 77, 67)
(49, 73, 61, 76, 51, 75, 59, 74).
9.2.1 The involutory Progenitor 2
∗
80
: (2
•
A
6
)
To write a presentation for the progenitor of 2
•
A
6
, we have to introduce a new
variable t = t
1
of order 2, and find all elements of N that stabilise 1. By using MAGMA,
we obtain the following
(3, 28, 37)(6, 22, 46)(7, 36, 33)(8, 17, 56)(9, 59, 10)(11, 27, 39)(12, 61, 18)(13, 23, 48)
(14, 35, 31)(15, 16, 58)(19, 51, 20)(21, 49, 24)(25, 75, 62)(26, 74, 52)(29, 73, 63)(30, 76, 53)
(32, 72, 44)(34, 70, 43)(38, 80, 42)(40, 79, 41)(45, 54, 77)(47, 50, 78)(55, 64, 71)
(57, 60, 69) = xy
2
xy
−1
(3, 48, 19)(6, 49, 27)(7, 58, 12)(8, 59, 35)(9, 14, 56)(10, 31, 17)(11, 46, 21)(13, 51, 28)
(15, 61, 36)(16, 18, 33)(20, 37, 23)(22, 24, 39)(25, 44, 54)(26, 41, 60)(29, 43, 50)(30, 42, 64)
(32, 77, 75)(34, 78, 73)(38, 71, 76)(40, 69, 74)(45, 62, 72)(47, 63, 70)(52, 79, 57)
(53, 80, 55) = y
2
xy
−1
xyxy
2
x

150
Now, we have to insert t and with which commutes into our progenitors. Then the
presentation for 2
∗
80
: (2
•
A
6
) is
hx, y, t|x
4
, y
8
, (xy)
5
, (xy
2
)
5
, (y
4
, x), (x
2
, y), t
2
, (t, xy
2
xy
−1
), (t, y
2
xy
−1
xyxy
2
x)i
In order to make this progenitor finite, we factor it by some relation. To search for
relations, we use the following two methods
• All first order relations.
By using MAGMA, we obtain a list of the conjugacy classes of N = 2
•
A
6
.
Table 9.4: Conjugacy Classes of N = 2
•
A
6
Class Representitive of # Elements of Some Elements of
the Class form πt
i
form πt
i
2 x
2
1 x
2
t
1
3 xyxy
2
xy
−1
8 xyxy
2
xy
−1
t
i
, i = 1, 2, 3, 7
4 y
−1
xy
2
xyx 8 y
−1
xy
2
xyxt
i
, i = 1, 2, 3, 7
5 x 10 xt
1
, xt
3
, xt
7
6 xy 8 xyt
1
, xyt
2
7 (xy)
2
8 (xy)
2
t
1
, (xy)
2
t
2
8 xyxy
2
x
−1
y
−1
8 xyxy
2
x
−1
y
−1
t
i
, i = 1, 2, 3, 7
9 xy
−1
xy
2
x
−1
y 8 xy
−1
xy
2
x
−1
yt
i
, i = 1, 2, 3, 7
10 y 10 yt
1
,yt
2
11 x
2
y
−1
10 x
2
y
−1
t
1
, x
2
y
−1
t
2
12 xy
−1
8 xy
−1
t
1
, xy
−1
t
2
, xy
−1
t
3
,t
7
13 yxyx
−1
8 yxyx
−1
t
i
, i = 1, 2, 3, 7
Since t ≈ t
1
, we get
t
2
= t
x
, t
3
= t
y
, and t
7
= t
x
y
• Apply the Lemma.
By finding the centralizer of two points stabiliser t
1
and t
2
, we obtain three gen-
erators, thus we choose to factor by the relation
(3, 28, 37)(6, 22, 46)(7, 36, 33) . . . (47, 50, 78)(55, 64, 71)(57, 60, 69) = xyxy
2
xy
−1
(3, 48, 19)(6, 49, 27)(7, 58, 12) . . . (47, 63, 70)(52, 79, 57)(53, 80, 55) = y
2
xy
−1
xyxy
2
x
Thus, the short relations are given by

151
(t
1
t
2
)
k
= (tt
x
)
k
= xyxy
2
xy
−1
.
(t
1
t
2
)
l
= (tt
x
)
l
= y
2
xy
−1
xyxy
2
x.
In order to have some finite images, we factored the progenitor by some of the relations
from the conjugacy classes table and the lemma but no interesting homomorphic images
were obtained.
9.2.2 Monomial Progenitor 17
∗
10
:
m
(2
•
A
6
)
Consider the group 17
∗
10
:
m
(2
•
A
6
), where G = 2
•
A
6
. The presentation for G
is given by hx, y|x
4
, y
8
, (xy)
5
, (xy
2
)
5
, (y
4
, x), (x
2
, y)i. To write a monomial presentation
for G, we chose a subgroup H = 3
2
•
8 of G and induced it up by a faithful irreducible
linear character χ
5
.
Table 9.5: Character Table of G = 2
•
A
6
χ C
1
C
2
C
3
C
4
C
5
C
6
C
7
C
8
C
9
C
10
C
11
C
12
C
13
χ
13
10 -10 1 1 0 0 0 -1 -1 −Z2 Z2 0 0
# denotes algebraic conjugation
I = RootOfUnity(4)
Z
1
is the primitive eigth root of unity
Table 9.6: Character Table of H = 3
2
•
8
χ C
1
C
2
C
3
C
4
C
5
C
6
C
7
C
8
C
9
C
10
C
11
C
12
χ
1
1 1 1 1 1 1 1 1 1 1 1 1
χ
2
1 1 1 1 1 1 1 1 -1 -1 -1 -1
χ
3
1 1 1 1 -1 -1 1 1 −I I −I I
χ
4
1 1 1 1 -1 -1 1 1 I −I I −I
χ
5
1 -1 1 1 I −I -1 -1 Z1 Z1#3 −Z1 −Z1#3
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
χ
12
4 4 -2 1 0 0 -2 1 0 0 0 0
I = RootOfUnity(4)
To find the value of I, we have to determine the smallest finite field that has
the fourth roots of unity. We find that it is F
17
. Moreover, since the primitive root of

152
17 is 3, we know that |3| = 16. Also, to know the value for different powers of I, we
apply the following formula
|3
k
| =
16
gcd(k, 16)
Thus, |3
2
| =
16
gcd(2,16)
=
16
2
= 8. Now, we have that (3
2
)
8
= 9
8
≡
17
1. By taking I = 9,
the value for the different powers of I is as the following:
I
2
= 9
2
= 81 ≡
17
13
I
3
= 9
3
= 729 ≡
17
15
I
4
≡
17
1
Now, we can find the two induced representation A(x) and A(y) of degree
|G|
|N|
=
720
72
= 10
of G.
A(x) =
0 1 0 0 0 0 0 0 0 0
−1 0 0 0 0 0 0 0 0 0
0 0 0 1 0 0 0 0 0 0
0 0 −1 0 0 0 0 0 0 0
0 0 0 0 −13 0 0 0 0 0
0 0 0 0 0 0 0 −1 0 0
0 0 0 0 0 0 0 0 0 1
0 0 0 0 0 1 0 0 0 0
0 0 0 0 0 0 0 0 13 0
0 0 0 0 0 0 −1 0 0 0
and
A(y) =
0 0 −1 0 0 0 0 0 0 0
0 0 0 15 0 0 0 0 0 0
0 0 0 0 1 0 0 0 0 0
0 0 0 0 0 −15 0 0 0 0
0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 0 −15 0
1 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 9 0 0
0 15 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 −15

153
A(x) and A(y) are monomial matrices since there is a non-zero entry in each row and
column. By checking the order of the two matrices, we see that |A(x)| = 4 = |x|,
|A(y)| = 8 = |y|, |A(x) ∗ A(y)| = 5 = |xy|, |A(x) ∗ A(y)
2
| = 5 = |xy
2
|, |(A(x)
2
, A(y))| =
1 = |(x
2
, y)|, and |(A(y)
4
, A(x))| = 1 = |(y
4
, x)| . hA(x), A(y)i is a faithful representa-
tion of 2
•
A
6
. Now, we want to write permutation representation of the two monomial
matrices. Elements of the free product 17
∗
10
is of the form < t
1
> ∗ < t
2
> ∗ . . . ∗ <
t
9
> ∗ < t
10
>, where |t
i
| = 3 and < t
i
>= {e, t
i
, t
i
2
, . . . , t
i
16
} for ∀1 ≤ i ≤ 10.
Table 9.7: Labeling for t
i
’s
1 2 3 4 5 · · · 12 13 14 15 16
t
1
→ t
1
t
1
2
t
1
3
t
1
4
t
1
5
· · · t
1
12
t
1
13
t
1
14
t
1
15
t
1
16
17 18 19 20 21 · · · 28 29 30 31 32
t
2
→ t
2
t
2
2
t
2
3
t
2
4
t
2
5
· · · t
2
12
t
2
13
t
2
14
t
2
15
t
2
16
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. · · ·
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
145 146 147 148 149 · · · 156 157 158 159 160
t
10
→ t
10
t
10
2
t
10
3
t
10
4
t
10
5
· · · t
10
12
t
10
13
t
10
14
t
10
15
t
10
16
To determine the permutaion for x = A(x), we looke at the nonzero entry a
i,j
of A(x)
such that
a
1,2
= 1 ⇒ the automorphism takes t
1
→ t
2
, so A(x) takes 1 to 17 in our labeling
above.
Moreover, when t
1
2
→ t
2
2
, A(x) takes 2 to 18, and so on with the all powers of t
1
.
a
2,1
= −1 ≡
17
16 ⇒ the automorphism takes t
2
→ t
1
16
,so A(x) takes 17 to 16.
Moreover, when t
2
2
→ t
16×2
1
≡
17
t
15
1
, A(x) takes 18 to 15.
.
.
.

154
Table 9.8: Permutaion of x = A(x)
1 2 3 4 5 · · · 12 13 14 15 16
t
1
→ t
1
t
1
2
t
1
3
t
1
4
t
1
5
· · · t
1
12
t
1
13
t
1
14
t
1
15
t
1
16
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
t
2
t
2
2
t
2
3
t
2
4
t
2
5
· · · t
2
12
t
2
13
t
2
14
t
2
15
t
2
16
17 18 19 20 21 · · · 28 29 30 31 32
129 130 131 132 133 · · · 140 141 142 143 144
t
9
→ t
9
t
9
2
t
9
3
t
9
4
t
9
5
· · · t
9
12
t
9
13
t
9
14
t
9
15
t
9
16
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
t
13
9
t
9
9
t
9
5
t
9
t
9
14
· · · t
9
3
t
9
16
t
9
12
t
9
8
t
9
4
141 137 133 129 142 · · · 131 144 140 136 132
145 146 147 148 149 · · · 156 157 158 159 160
t
10
→ t
10
t
10
2
t
10
3
t
10
4
t
10
5
· · · t
10
12
t
10
13
t
10
14
t
10
15
t
10
16
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
t
7
16
t
7
15
t
7
14
t
7
13
t
7
12
· · · t
7
5
t
7
4
t
7
3
t
7
2
t
7
112 111 110 109 108 · · · 101 100 99 98 97
The permutaion of A(x) is
x ≈(1, 17, 16, 32)(2, 18, 15, 31)(3, 19, 14, 30)(4, 20, 13, 29)(5, 21, 12, 28)(6, 22, 11, 27)
(7, 23, 10, 26)(8, 24, 9, 25)(33, 49, 48, 64)(34, 50, 47, 63)(35, 51, 46, 62)(36, 52, 45, 61)
(37, 53, 44, 60)(38, 54, 43, 59)(39, 55, 42, 58)(40, 56, 41, 57)(65, 68, 80, 77)
(66, 72, 79, 73)(67, 76, 78, 69)(70, 71, 75, 74)(81, 128, 96, 113)(82, 127, 95, 114)
(83, 126, 94, 115)(84, 125, 93, 116)(85, 124, 92, 117)(86, 123, 91, 118)
(87, 122, 90, 119)(88, 121, 89, 120)(97, 145, 112, 160)(98, 146, 111, 159)
(99, 147, 110, 158)(100, 148, 109, 157)(101, 149, 108, 156)(102, 150, 107, 155)
(103, 151, 106, 154)(104, 152, 105, 153)(129, 141, 144, 132)(130, 137, 143, 136)
(131, 133, 142, 140)(134, 138, 139, 135)
Similarly for the permutation of y = A(y). The permutation for A(y) is

155
Table 9.9: Permutaion of y = A(y)
1 2 3 4 5 · · · 12 13 14 15 16
t
1
→ t
1
t
1
2
t
1
3
t
1
4
t
1
5
· · · t
1
12
t
1
13
t
1
14
t
1
15
t
1
16
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
t
3
16
t
3
15
t
3
14
t
3
13
t
3
12
· · · t
3
5
t
3
4
t
3
3
t
3
2
t
3
48 47 46 45 44 · · · 37 36 35 34 33
129 130 131 132 133 · · · 140 141 142 143 144
t
9
→ t
9
t
9
2
t
9
3
t
9
4
t
9
5
· · · t
9
12
t
9
13
t
9
14
t
9
15
t
9
16
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
t
2
15
t
2
13
t
2
11
t
2
9
t
2
7
· · · t
2
12
t
2
10
t
2
8
t
2
4
t
2
2
31 29 27 25 23 · · · 26 24 22 20 18
145 146 147 148 149 · · · 156 157 158 159 160
t
10
→ t
10
t
10
2
t
10
3
t
10
4
t
10
5
· · · t
10
12
t
10
13
t
10
14
t
10
15
t
10
16
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
t
2
10
t
10
4
t
10
6
t
10
8
t
10
10
· · · t
10
7
t
10
9
t
10
11
t
10
13
t
10
15
146 148 150 152 154 · · · 151 153 155 157 159
y ≈(1, 48, 80, 112, 16, 33, 65, 97)(2, 47, 79, 111, 15, 34, 66, 98)
(3, 46, 78, 110, 14, 35, 67, 99)(4, 45, 77, 109, 13, 36, 68, 100)
(5, 44, 76, 108, 12, 37, 69, 101)(6, 43, 75, 107, 11, 38, 70, 102)
(7, 42, 74, 106, 10, 39, 71, 103)(8, 41, 73, 105, 9, 40, 72, 104)
(17, 63, 93, 137, 32, 50, 84, 136)(18, 61, 89, 129, 31, 52, 88, 144)
(19, 59, 85, 138, 30, 54, 92, 135)(20, 57, 81, 130, 29, 56, 96, 143)
(21, 55, 94, 139, 28, 58, 83, 134)(22, 53, 90, 131, 27, 60, 87, 142)
(23, 51, 86, 140, 26, 62, 91, 133)(24, 49, 82, 132, 25, 64, 95, 141)
(113, 121, 125, 127, 128, 120, 116, 114)(115, 122, 117, 123, 126, 119, 124, 118)
(145, 146, 148, 152, 160, 159, 157, 153)(147, 150, 156, 151, 158, 155, 149, 154)
Now, we want to write a presentation for the monoial progenitor 17
∗
10
:
m
(2
•
A
6
). Let
t ≈ t
1
. By using MAGMA, the normliser of the subgroup < t
1
> is generated by
(17, 104, 152) . . . (64, 66, 95) = yxy
−1
xyxy
2
xyx,
(17, 125, 49) . . . (96, 157, 132) = xyxy
2
xy
−1
x
−1
y, and
(1, 9, 13, 15, 16, 8, 4, 2) . . . (147, 150, 156, 151, 158, 155, 149, 154) = xyxy
2
xy
−1
xy
2
xy
−1
x.
156
Thus, a presentation for the monomial progenitor is given by
17
∗
10
:
m
(2
•
A
6
) = hx, y, t|x
4
, y
8
, (xy)
5
, (xy
2
)
5
, (x
2
, y), (y
4
, x), t
17
,
(t, yxy
−1
xyxy
2
xyx), (t, xyxy
2
xy
−1
x
−1
y), t
xyxy
2
xy
−1
xy
2
xy
−1
x
t
−9
i.
We want to obtain 17
10
: (2
•
A
6
) as a homomorphic image of 17
∗
10
:
m
(2
•
A
6
). Thus, we
factor the progenitor 17
∗
10
:
m
(2
•
A
6
) by the following commutators, but it seemed hard
to prove it as an isomorphic image of 17
∗
10
:
m
(2
•
A
6
).
(t, t
x
), (t, t
x
2
y
), (t, t
yx
−1
), (t, t
y
−2
), (t, t
(xy
−1
)
2
),
(t, t
y
−1
), (t, t
(xy
2
)
2
), (t, t
yxy
2
x
−1
), (t, t
y
−1
x
).
9.3 3
•
A
6
Consider the group
N = 3
•
A
6
= hx, y|x
2
, y
4
, (xy)
15
, (xy
2
)
5
, ((xy)
5
, x), ((xy)
5
, y)i,
where
x ≈(2, 6)(4, 11)(7, 9)(8, 13)(10, 14)(12, 16).
y ≈(1, 2, 7, 4)(3, 8, 6, 10)(5, 9, 13, 12)(11, 15)(14, 17)(16, 18).
9.3.1 The involutory Progenitor 2
∗
18
: (3
•
A
6
)
To write a presentation for this type of progenitor, we must introduce a new
variable t = t
1
of order 2, and find all elements of N that stabilise 1. By using MAGMA,
we obtain the following
(2, 6)(4, 11)(7, 9)(8, 13)(10, 14)(12, 16) = x
(2, 7, 17, 10, 16)(4, 14, 9, 13, 15)(6, 18, 12, 11, 8) = (y
2
xy
−1
)
3
.
Since t commutes with each generator of the one point stabiliser, we have to insert t
and with which commutes into our progenitors. Then the presentation for 2
∗
18
: (3
•
A
6
)
is
hx, y, t|x
4
, y
3
, (xy)
5
, (x
2
, y), t
2
, (t, x), (t, (y
2
xy
−1
)
3
)i.
In order to search for relations, we use the following two methods

157
• Factor the progenitor by some of the first order relations.
By using MAGMA, we obtain a list of the conjugacy classes of N = 3
•
A
6
.
Table 9.10: Conjugacy Classes of N = 3
•
A
6
Class Representitive of the Class Elements of form πt
i
2 y
2
y
2
t
1
,y
2
t
11
6 xy
2
xyxyxy
−1
xy
2
xyxyxy
−1
t
i
, i = 1, 2, 6, 11
12 yxy
−1
xyx yxy
−1
xyxt
i
, i = 1, 2
Since t ≈ t
1
, we get
t
2
= t
y
, t
6
= t
yx
, t
11
= t
y
−1
x
• Apply the Lemma.
We will utilize the lemma by taking the stabiliser of two elements and determin-
ing the centraliser of those points. The lemma deals with elements that have a
transposition (1,2), or do have either 1 or 2, or do not have either of them.
N ∩ ht
0
, t
1
i ≤ C
N
(N
01
).
N
(01)
= hei.
C
N
(N
01
) = hy
−1
xy
−1
xy
2
xyxy, y
2
xy
−1
xyxy
2
i.
By adding all the relations from the above table and write some supporting relations,
the presentation for this progenitor is
< x, y, t|x
2
, y
4
, (xy
2
)
5
, (xy)
1
5, ((xy)
5
, x), ((xy)
5
, y), t
2
, (t, x), (t, (y
2
xy
−
1)
3
),
(tt
y
)
k
= y
−1
xy
−1
xy
2
xyxy, (y
2
t)
l
, (y
2
t
y
−1
x
)
m
, (xy
2
xyxyxy
−1
t)
n
, (xy
2
xyxyxy
−1
t
yx
)
o
,
(xy
2
xyxyxy
−1
t
y
−1
x
)
p
, (xy
2
xyxyxy
−1
t
y
)
q
, (yxy
−1
xyxt)
r
, (yxy
−1
xyxt
y
)
u
> .
The progenitor 2
∗
18
: (3
•
A
6
) faild to construct any homomorphic images.
9.3.2 Monomial Progenitor 7
∗
6
:
m
(3
•
A
6
)
Consider the group 7
∗
6
:
m
(3
•
A
6
), where G = 3
•
A
6
. The presentation for
G is given by hx, y|x
2
, y
4
, (xy)
15
, (xy
2
)
5
, ((xy)
5
, x), ((xy)
5
, y)i. To write a monomial
presentation for G, we chose a subgroup H = 3 × A
5
of G and induced it up by a

158
Table 9.11: Character Table of G = 3
•
A
6
χ C
1
C
2
C
3
C
4
· · · C
14
C
15
C
16
C
17
χ
9
6 2 6 ∗ J −6 − 6 ∗ J · · · −1 − J J −1 − J J
# denotes algebraic conjugation
J = RootOfUnity(3)
faithful irreducible linear character χ
3
= (1, 1, J, −1−J, −1−J, J, 1, 1, 1, −1−J, J, J, −1−
J, J, −1 − J). To find the value of J, we have to determine the smallest finite field that
has the cube roots of unity. We find that it is F
7
. Thus, the value for J and J
2
is 2 and
4, respictivelly. By inducing the theird linear character of H up to G, we can find the
two induced representation A(x) and A(y) of degree
|G|
|H|
=
1080
180
= 6 of G.
A(x) =
0 4 0 0 0 0
2 0 0 0 0 0
0 0 1 0 0 0
0 0 0 0 1 0
0 0 0 1 0 0
0 0 0 0 0 1
and
A(y) =
0 0 1 0 0 0
1 0 0 0 0 0
0 0 0 1 0 0
0 1 0 0 0 0
0 0 0 0 0 4
0 0 0 0 2 0
A(x) and A(y) are monomial matrices since there is a non-zero entry in each row and
column. The two maonomial matrices are faithful since they satisfed the following
|A(x)| = 2 = |x|, |A(y)| = 4 = |y|, |A(x) ∗ A(y)| = 15 = |xy|, |A(x) ∗ A(y)
2
| = 5 = |xy
2
|,
|((A(x)A(y))
5
, A(y))| = 1 = |((xy)
5
, y)|, and |((A(x)A(y))
5
, A(x))| = 1 = |((xy)
5
, x)|.
hA(x), A(y)i is a faithful representation of 3
•
A
6
. Now, we want to write permutation
representation of the two monomial matrices. Elements of the free product 7
∗
6
is of

159
the form < t
1
> ∗ < t
2
> ∗ . . . ∗ < t
5
> ∗ < t
6
>, where |t
i
| = 7 and < t
i
>=
{e, t
i
, t
i
2
, . . . , t
i
6
} for ∀1 ≤ i ≤ 6.
Table 9.12: Labeling for t
i
’s
1 2 3 4 5 6 7 8 9 10 11 12
t
1
t
1
2
t
1
3
t
1
4
t
1
5
t
1
6
t
2
t
2
2
t
2
3
t
2
4
t
2
5
t
2
6
13 14 15 16 17 18 19 20 21 22 23 24
t
3
t
3
2
t
3
3
t
3
4
t
3
5
t
3
6
t
4
t
4
2
t
4
3
t
4
4
t
4
5
t
4
6
25 26 27 28 29 30 31 32 33 34 35 36
t
5
t
5
2
t
5
3
t
5
4
t
5
5
t
5
6
t
6
t
6
2
t
6
3
t
6
4
t
6
5
t
6
6
By looking at the non-zero entry a
i,j
of A(x), we can determine the permutaion for
x = A(x).
a
1,2
= 4 ⇒ the automorphism takes t
1
→ t
2
4
, so A(x) takes 1 to 10.
Moreover, when t
1
2
→ t
2
4×2
≡
7
t
2
, A(x) takes 2 to 7
and so on with the all powers of t
1
. a
2,1
= 2 ⇒ the automorphism takes t
2
→ t
1
2
,so
A(x) takes 7 to 2.
Moreover, when t
2
2
→ t
2×2
1
= t
1
4
, A(x) takes 8 to 4
.
.
.
Table 9.13: Permutaion of x = A(x)
1 2 3 4 5 6 · · · 31 32 33 34 35 36
t
1
t
1
2
t
1
3
t
1
4
t
1
5
t
1
6
· · · t
6
t
6
2
t
6
3
t
6
4
t
6
5
t
6
6
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
t
2
4
t
2
t
2
5
t
2
2
t
2
6
t
2
3
· · · t
6
t
6
2
t
6
3
t
6
4
t
6
5
t
6
6
10 7 11 8 12 9 · · · 31 32 33 34 35 36
The permutaion of A(x) is
x ≈ (1, 10)(2, 7)(3, 11)(4, 8)(5, 12)(6, 9)(19, 25)(20, 26)(21, 27)(22, 28)(23, 29)(24, 30).
Similarly for the permutation of y = A(y). The permutation for A(y) is

160
Table 9.14: Permutaion of y = A(y)
1 2 3 4 5 6 · · · 31 32 33 34 35 36
t
1
t
1
2
t
1
3
t
1
4
t
1
5
t
1
6
· · · t
6
t
6
2
t
6
3
t
6
4
t
6
5
t
6
6
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
t
3
t
3
2
t
3
3
t
3
4
t
3
5
t
3
6
· · · t
5
2
t
5
4
t
5
6
t
5
t
5
3
t
5
5
13 14 15 16 17 18 · · · 26 28 30 25 27 29
y ≈ (1, 13, 19, 7)(2, 14, 20, 8)(3, 15, 21, 9)(4, 16, 22, 10)
(5, 17, 23, 11)(6, 18, 24, 12)(25, 34)(26, 31)
(27, 35)(28, 32)(29, 36)(30, 33)
Now, we want to write a presentation for the monoial progenitor 7
∗
6
:
m
(3
•
A
6
). Let
t ≈ t
1
. By using MAGMA, the normlisers of the subgroup < t
1
> that fixes t
1
and its
powers is generated by
(13, 31)(14, 32)(15, 33) . . . (22, 28)(23, 29)(24, 30) = y
2
xyxy
2
xy
−1
xy
2
.
(13, 19)(14, 20)(15, 21) . . . (28, 34)(29, 35)(30, 36) = y
−1
xy
−1
xyxy
2
x.
(7, 10, 8)(9, 11, 12) . . . (25, 26, 28)(27, 30, 29) = xyxyxy
2
xy
−1
.
(7, 14)(8, 16)(9, 18) . . . (22, 31)(23, 33)(24, 35) = y
2
xy
−1
xyxy
2
.
(1, 4, 2)(3, 5, 6) . . . (19, 20, 22)(21, 24, 23) = xy
−1
xy
−1
xyxy
2
.
By looking to the above permutations, we see that the last one is the only one that
takes t
1
to t
4
1
(from labeling). Thus, it will have the following form
t
xy
−1
xy
−1
xyxy
2
= t
4
Thus, a presentation for the monomial progenitor is given by
7
∗
6
:
m
(3
•
A
6
) = hx, y, t|x
2
, y
4
, (xy)
15
, (xy
2
)
5
, ((xy)
5
, y), ((xy)
5
, x), t
7
, (t, y
−1
xyxy
−1
xy),
(t, y
2
xyxy
2
xy
−1
xy
2
), (t, y
−1
xy
−1
xyxy
2
x), (t, y
2
xy
−1
xyxy
2
),
t
xy
−1
xy
−
1xyxy
2
t
−4
i.
To make this progenitor finite, we factored it by (t, t
x
) and (t, t
(xy)
−1
). Thus, we were
able to obtain the following homomorphic image
7
∗
6
:
m
(3
•
A
6
)
(t,t
x
),(t,t
(xy)
−1
)
∼
=
7
6
: (3
•
A
6
)

161
9.4 6
•
A
6
Consider the group
N = 6
•
A
6
= hx, y|x
2
= y
4
, (xy)
5
= (y
4
(xy)
5
)
−2
, (xy
2
)
5
, (y
4
(xy)
5
, x), (y
4
(xy)
5
, y)i,
where
x ≈ (1, 2, 8, 5)(3, 13, 22, 16)(4, 10, 9, 19) · · · (421, 422, 423, 424)(427, 430, 428, 429).
y ≈ (1, 3, 14, 12, 8, 22, 21, 6)(2, 9, 23, 20, 5, 4, 15, 11) · · · (395, 421, 431, 424, 396,
423, 432, 422).
9.4.1 The involutory Progenitor 2
∗
432
: (6
•
A
6
)
To write a presentation for the progenitor of 6
•
A
6
, we have to introduce a new
variable t = t
1
of order 2, and find all elements of N that stabilise 1. By using MAGMA,
the stabiliser of t
1
is the identity. The presentation for 2
∗
432
: (6
•
A
6
) is
hx, y, t|x
2
= y
4
, (xy)
5
= (y
4
(xy)
5
)
−2
, (xy
2
)
5
, (y
4
(xy)
5
, x), (y
4
(xy)
5
, y), t
2
i.
In order to make this progenitor finite, we factor it by some relation. To search for
relations, we use the following two methods
• Some of the first order relations.
By using MAGMA, we obtain a list of the conjugacy classes of N = 6
•
A
6
.
Table 9.15: Conjugacy Classes of N = 6
•
A
6
Class Representitive of the Class Some Elements of form πt
i
18 xyxy
−1
xy
−1
xy
−1
xy
−1
xyxy
−1
xy
−1
xy
−1
xy
−1
t
i
, i = 1, 3, 14
20 xy xyt
1
,xyt
2
,xyt
14
26 yxyxyx
−1
y yxyxyx
−1
yt
i
, i = 1, 3, 14
31 xy
−1
xy
−1
t
1
,xy
−1
t
2
,xy
−1
t
3
Since t ≈ t
1
, we get
t
2
= t
x
, t
3
= t
y
, and t
14
= t
y
2
• Apply the Lemma.
By finding the centralizer of two points stabiliser t
1
and t
2
, we find it is the whole
group G. Thus, we are not going to use the lemma for this progenitor.

162
Therefore, by adding all of the relations from the conjugacy classes table, the presenta-
tion for the progenitor 2
∗
432
: (6
•
A
6
) is
< x, y, t|x
2
= y
4
, (xy)
5
= (y
4
(xy)
5
)
−2
, (xy
2
)
5
, (y
4
(xy)
5
, x), (y
4
(xy)
5
, y), t
2
,
(xyxy
−1
xy
−1
xy
−1
xy
−1
t)
k
, (xyxy
−1
xy
−1
xy
−1
xy
−1
t
y
)
l
, (xyxy
−1
xy
−1
xy
−1
xy
−1
t
y
2
)
m
,
(xyt)
n
, (xyt
x
)
o
, (xyt
y
2
)
p
, (yxyxyx
−1
yt)
q
, (yxyxyx
−1
yt
y
)
r
, (yxyxyx
−1
yt
y
2
)
s
, (xy
−1
t)
u
,
(xy
−1
t
x
)
v
, (xy
−1
t
y
)
w
> .
By running the above presentation, we find some finit images as given in the Table 9.16.
Table 9.16: Some finite images of the progenitor 2
∗
432
: (6
•
A
6
)
k l · · · s u v w Index in G Order of G Shape of G
0 0 · · · 0 3 2 5 360 129600 A
6
: A
6
0 0 · · · 0 2 2 16 2 4320 (2 × 3)•P GL
2
(9)
9.4.2 Monomial Progenitor 61
∗
36
:
m
(6
•
A
6
)
Consider the group 61
∗
36
:
m
(6
•
A
6
), where G = 6
•
A
6
. The presentation for G
is given by hx, y|x
2
= y
4
, (xy)
5
= (y
4
(xy)
5
)
−2
, (xy
2
)
5
, (y
4
(xy)
5
, x), (y
4
(xy)
5
, y)i.
we want to write a presentation for the monomial progenitor of 6
•
A
6
, so we want to
induce a faithful linear character (not necessarily irrducible) from a subgroup H up to
6
•
A
6
. To do, we run the following loop
> S:=Subgroups(G1);
> #S;
51
So, we have investigated all the subgroup S[i] where 25 ≤ i ≤ 51 of 6
•
A
6
, and we
find that the only subgroup that contain a faithful (not irreducible) linear character are
those of index n equal to 36, 60, 90 and 72. Since the degree of the monomial matrices
is n implies that we will have n × n matrices, we consider to induce that one with lower
index 36.
Now, we will induce the 9
th
linear character of H = (3 × 2 × 5) : 2 of order 60 up to

163
Group Subgroup, Index, and Linear Representation Linear Characters
6
•
A
6
37, 36, (3 × 2 × 5) : 2 χ
1
→ χ
12
χ
2
→ χ
8
nonfaithful
χ
9
→ χ
12
faithful
6
•
A
6
.
χ
(9)
= (1, −1, J, −1 − J, −I, I, 1, 1, 1 + J, −J, −1, −1, Z2, Z2
5
, −Z, 2 − Z2
5
, J, −1 − J, J,
−1 − J, 1 + J, 1 + J, −J, −J),
where
J is the cube root of unity
I is the fourth root of unity
Z
1
is the primitive 5
th
root of unity
Z
2
is the primitive 12
th
root of unity
Z
3
is the primitive 15
th
root of unity
The smallest finite field that divisible by 5, 12, and 15 is F
61
and the primitive root of
61 is 2. To find the third and fourth root of unity J and I, respectivelly, we have to
find k
1
and k
2
that satisfied the following
|2
k
1
| =
60
gcd(k
1
, 60)
= 3. Thus, k
1
=
60
3
= 20.
|2
k
2
| =
60
gcd(k
2
, 60)
= 4. Thus, k
2
=
60
4
= 15.
Hence,
J = 2
20
≡
61
47 and J
2
= 47
2
≡
61
13.
I = 2
15
≡
61
11, I
2
= 11
2
≡
61
60, and I
3
= 11
3
≡
61
50.
The elements of order 3 are 47 and 13, and the elements of order 4 are 11, 60, and 50.
To find monomial matrices A(x) and A(y), we have to find the 36 non-zero entries of
both matrices by running the following loops
A:=[0:i in [1..1296]];
for i in [1..36] do if a
*
T[i]ˆ-1 in N then i,
chN[9](a
*
T[i]ˆ-1); end if; end for;
for i in [1..36] do if T[2]
*
a
*
T[i]ˆ-1 in N then i,
164
chN[9](T[2]
*
a
*
T[i]ˆ-1); end if; end for;
B:=[0:i in [1..1296]];
for i in [1..36] do if b
*
T[i]ˆ-1 in N then i,
chN[9](b
*
T[i]ˆ-1); end if; end for;
for i in [1..36] do if T[2]
*
b
*
T[i]ˆ-1 in N then i,
chN[9](T[2]
*
b
*
T[i]ˆ-1); end if; end for;
We will mention the non-zero entries of the two matrices A(x) and A(y) (see table 9.17).

165
Table 9.17: Nonzero Entries of A(x) and A(y)
A(x) A(y)
Row n Entry Value Entry Value
1 2 −J = −47 3 −J = −47
2 1 −J − 1 = J
2
= 13 5 −J = −47
3 8 1 8 I + 1 = −I
2
= −13
4 4 I = 11 11 1
5 14 −J − 1 = J
2
= 13 12 1
6 16 −J − 1 = J
2
= 13 17 −J = −47
7 7 −I = −11 20 −J = −47
8 3 -1 10 J = 47
9 24 −J − 1 = J
2
= 13 6 1
10 26 −J = −47 1 J + 1 = −J
2
= −13
11 27 1 4 −I = −11
12 28 -1 29 1
13 32 1 33 -1
14 5 −J = −47 24 −J − 1 = J
2
= 13
15 23 1 34 −J − 1 = J
2
= 13
16 6 −J = −47 26 1
17 30 -1 35 1
18 20 1 30 J + 1 = −J
2
= −13
19 33 -1 18 1
20 18 -1 14 1
21 25 1 31 J + 1 = −J
2
= −13
22 36 -1 19 J = 47
23 15 -1 16 −J − 1 = J
2
= 13
24 9 −J = −47 7 1
25 21 -1 23 1
26 10 −J − 1 = J
2
= 13 25 −J = −47
27 11 -1 36 1
28 12 1 32 1
29 31 1 2 −J − 1 = J
2
= 13
30 17 1 22 1
31 29 -1 21 −IJ = −29
32 13 -1 15 1
33 19 1 27 1
34 34 I = 11 28 −J = −47
35 35 −I = −11 9 −J − 1 = J
2
= 13
36 22 1 13 1
166
Appendix A: MAGMA Code for
DCE of S
5
over A
4
/
*
This is S5 homographic image of the progenitor
2star4:A4(4 double cosets,10 single cosets)
*
/
-----------------------------------------------------
S:=Sym(4);
xx:=S!(1,2)(3,4);
yy:=S!(1,2,3);
N:=sub<S|xx,yy>;
Stabiliser(N,4);
#N;
G<x,y,t>:=Group<x,y,t|xˆ2,yˆ3,(x
*
y)ˆ3,tˆ2,(t,y),
((yˆ2)
*
x
*
t
*
(tˆx))ˆ2, (y
*
t
*
(tˆx)
*
tˆ(xˆ2))ˆ4>;
f,G1,k:=CosetAction(G,sub<G|x,y>);
IN:=sub<G1|f(x),f(y)>;
CompositionFactors(G1);
#DoubleCosets(G,sub<G|x,y>,sub<G|x,y>);
DoubleCosets(G,sub<G|x,y>,sub<G|x,y>);
NN<a,b>:=Group<a,b|aˆ2,bˆ3,(a
*
b)ˆ3>;
Sch:=SchreierSystem(NN,sub<NN|Id(NN)>);
ArrayP:=[Id(N): i in [1..12]];
for i in [2..12] do
P:=[Id(N): l in [1..#Sch[i]]];
for j in [1..#Sch[i]] do
if Eltseq(Sch[i])[j] eq 1 then P[j]:=xx; end if;
if Eltseq(Sch[i])[j] eq 2 then P[j]:=yy; end if;
if Eltseq(Sch[i])[j] eq -2 then P[j]:=yyˆ-1; end if;
end for;
PP:=Id(N);
for k in [1..#P] do
PP:=PP
*
P[k]; end for;
ArrayP[i]:=PP;
167
end for;
for i in [1..12] do if ArrayP[i] eq N!(1,2)(3,4)
then Sch[i];
end if; end for;
prodim := function(pt, Q, I)
/
*
Return the image of pt under permutations Q[I]
applied sequentially.
*
/
v:=pt;
for i in I do
v:=vˆ(Q[i]);
end for;
return v;
end function;
ts:= [Id(G1): i in [1 .. 4] ];
ts[4]:=f(t); ts[1]:=f((tˆx)ˆy);
ts[2]:=ts[1]ˆf(y); ts[3]:=f(tˆ(x));
-----------------------------------------------------
/
*
This cst function will keep track of all
single cosets
*
/
cst:= [null : i in [1 .. Index(G,sub<G|x,y>)]]
where null is[Integers() |];
for i := 1 to 4 do
cst[prodim(1, ts, [i])]:=[i];
end for;
m:=0; for i in [1..10] do if cst[i] ne []
then m:=m+1; end if; end for; m;
-----------------------------------------------------
N0:=Stabiliser(N,4);
Orbits(N0);
#N0;
-----------------------------------------------------
N01:=Stabiliser(N,[4,1]);
SSS:={[4,1]};
SSS:=SSSˆN;
SSS;
#SSS;
Seqq:=Setseq(SSS);
Seqq;
for i in [1..#SSS] do
for n in IN do
if ts[4]
*
ts[1] eq
n
*
ts[Rep(Seqq[i])[1]]
*
ts[Rep(Seqq[i])[2]]
168
then print Rep(Seqq[i]);
end if; end for; end for;
N01s:=N01;
for n in N do if 4ˆn eq 4 and 1ˆn eq 2 then
N01s:=sub<N|N01s,n>; end if; end for;
for n in N do if 4ˆn eq 4 and 1ˆn eq 3 then
N01s:=sub<N|N01s,n>; end if; end for;
N01s; #N01s;
T01:=Transversal(N,N01);
for i in [1..#T01] do
ss:=[4,1]ˆT01[i];
cst[prodim(1, ts, ss)]:=ss;
end for;
m:=0; for i in [1..10] do if cst[i] ne []
then m:=m+1; end if; end for; m;
Orbits(N01s);
#N01s;
-----------------------------------------------------
N414:=Stabiliser(N,[4,1,4]);
SSS:={[4,1,4]}; SSS:=SSSˆN;
SSS;
#(SSS);
Seqq:=Setseq(SSS);
Seqq;
for i in [1..#SSS] do
for n in IN do
if ts[4]
*
ts[1]
*
ts[4] eq
n
*
ts[Rep(Seqq[i])[1]]
*
ts[Rep(Seqq[i])[2]]
*
ts[Rep(Seqq[i])[3]]
then print Rep(Seqq[i]);
end if; end for; end for;
N010s:=N414;
for n in N do if 4ˆn eq 2 then N010s:=sub<N|N010s,n>;
end if; end for;
for n in N do if 4ˆn eq 2 and 1ˆn eq 3 then
N010s:=sub<N|N010s,n>; end if; end for;
for n in N do if 4ˆn eq 1 and 1ˆn eq 4 then
N010s:=sub<N|N010s,n>; end if; end for;
for n in N do if 4ˆn eq 2 and 1ˆn eq 4 then
N010s:=sub<N|N010s,n>; end if; end for;
for n in N do if 4ˆn eq 3 and 1ˆn eq 2 then
N010s:=sub<N|N010s,n>; end if; end for;
for n in N do if 1ˆn eq 3 then
N010s:=sub<N|N010s,n>; end if; end for;
for n in N do if 4ˆn eq 3 and 1ˆn eq 4 then
169
N010s:=sub<N|N010s,n>; end if; end for;
for n in N do if 4ˆn eq 1 and 1ˆn eq 2 then
N010s:=sub<N|N010s,n>; end if; end for;
for n in N do if 1ˆn eq 2 then
N010s:=sub<N|N010s,n>; end if; end for;
for n in N do if 4ˆn eq 3 then
N010s:=sub<N|N010s,n>; end if; end for;
for n in N do if 4ˆn eq 1 and 1ˆn eq 3 then
N010s:=sub<N|N010s,n>; end if; end for;
N010s; #N010s;
T010:=Transversal(N,N010s);
for i in [1..#T010] do
ss:=[4,1,4]ˆT010[i];
cst[prodim(1,ts,ss)]:=ss;
end for;
m:=0; for i in [1..10] do if cst[i] ne []
then m:=m+1; end if; end for; m;
Orbits(N010s);
#(N010s);
-----------------------------------------------------
//
*
to print all single cosets
*
//
for i in [1..12] do i, cst[i]; end for;
170
Appendix B: MAGMA Code for
Isomorphism Type of S
5
S:=Sym(4);
xx:=S!(1,2)(3,4);
yy:=S!(1,2,3);
N:=sub<S|xx,yy>;
Stabiliser(N,4);
#N;
G<x,y,t>:=Group<x,y,t|xˆ2,yˆ3,(x
*
y)ˆ3,tˆ2,(t,y),
((yˆ2)
*
x
*
t
*
(tˆx))ˆ2, (y
*
t
*
(tˆx)
*
tˆ(xˆ2))ˆ4>;
f,G1,k:=CosetAction(G,sub<G|x,y>);
IN:=sub<G1|f(x),f(y)>;
CompositionFactors(G1);
Center(G1);
NL:=NormalLattice(G1);
NL;
MinimalNormalSubgroups(G1);
s,t:=IsIsomorphic(Alt(5),NL[2]);
s;
D:=DirectProduct(NL[2],NL[3]);
s,t:=IsIsomorphic(D,G1);
s;
H<a,b>:=Group<a,b|aˆ2,bˆ3,(a
*
b)ˆ5>;
#H;
f1,H1,k1:=CosetAction(H,sub<H|Id(H)>);
s,t:=IsIsomorphic(H1,NL[2]);
s;
s,t:=IsIsomorphic(H1,Alt(5));
s;
a:=NL[2].1;
b:=NL[2].2;
for g in G1 do if Order(g) eq 2 and g notin NL[2] and G1 eq
171
sub<G1|NL[2],g> then U:=g; break; end if; end for;
G1 eq sub<G1|NL[2],U>;
N:=sub<G1|a,b>;
#N;
NN<i,j>:=Group<i,j|iˆ2,jˆ3,(i
*
j)ˆ5>;
#NN;
Sch:=SchreierSystem(NN,sub<NN|Id(NN)>);
ArrayP:=[Id(N): i in [1..60]];
for i in [2..60] do
P:=[Id(N): l in [1..#Sch[i]]];
for j in [1..#Sch[i]] do
if Eltseq(Sch[i])[j] eq 1 then P[j]:=a; end if;
if Eltseq(Sch[i])[j] eq 2 then P[j]:=b; end if;
if Eltseq(Sch[i])[j] eq -2 then P[j]:=bˆ-1; end if;
end for;
PP:=Id(N);
for k in [1..#P] do
PP:=PP
*
P[k]; end for;
ArrayP[i]:=PP;
end for;
A:=[Id(NN): i in [1..2]];
for i in [1..60] do
if aˆU eq ArrayP[i] then A[1]:=Sch[i]; Sch[i]; end if;
end for;
for i in [1..60] do
if bˆU eq ArrayP[i] then A[2]:=Sch[i]; Sch[i]; end if;
end for;
HH<a,b,c>:=Group<a,b,c|aˆ2,bˆ3,(a
*
b)ˆ5,cˆ2,aˆc=a,
bˆc=a
*
bˆ-1
*
a
*
b
*
a
*
bˆ-1>;
#HH;
f2,H2,k:=CosetAction(HH,sub<HH|Id(HH)>);
s:=IsIsomorphic(H2,G1);
s;
s:=IsIsomorphic(H2,Sym(5));
s;
172
Appendix C: MAGMA Code for
DCE of L
2
(11) × 3 over A
4
/
*
This is $L(2,11)X3$ homographic image of the
progenitor 2star4:A4(20 double cosets)
*
/
-----------------------------------------------------
S:=Sym(4);
xx:=S!(1,2)(3,4);
yy:=S!(1,2,3);
N:=sub<S|xx,yy>;
Stabiliser(N,4);
#N;
G<x,y,t>:=Group<x,y,t|xˆ2,yˆ3,(x
*
y)ˆ3,(yˆ-1
*
xˆ-1
*
y
*
x)ˆ2,
tˆ2,(t,y),(x
*
t)ˆ5>;
f,G1,k:=CosetAction(G,sub<G|x,y>);
IN:=sub<G1|f(x),f(y)>;
CompositionFactors(G1);
#DoubleCosets(G,sub<G|x,y>,sub<G|x,y>);
DoubleCosets(G,sub<G|x,y>,sub<G|x,y>);
NN<a,b>:=Group<a,b|aˆ2,bˆ3,(a
*
b)ˆ3>;
Sch:=SchreierSystem(NN,sub<NN|Id(NN)>);
ArrayP:=[Id(N): i in [1..12]];
for i in [2..12] do
P:=[Id(N): l in [1..#Sch[i]]];
for j in [1..#Sch[i]] do
if Eltseq(Sch[i])[j] eq 1 then P[j]:=xx; end if;
if Eltseq(Sch[i])[j] eq 2 then P[j]:=yy; end if;
if Eltseq(Sch[i])[j] eq -2 then P[j]:=yyˆ-1; end if;
end for;
PP:=Id(N);
for k in [1..#P] do
PP:=PP
*
P[k]; end for;
ArrayP[i]:=PP;
173
end for;
for i in [1..12] do if ArrayP[i] eq N!(1,4)(2,3) then
Sch[i]; end if; end for;
prodim := function(pt, Q, I)
/
*
Return the image of pt under permutations Q[I]
applied sequentially.
*
/
v:=pt;
for i in I do
v:=vˆ(Q[i]);
end for;
return v;
end function;
ts:= [Id(G1): i in [1 .. 4] ];
ts[4]:=f(t); ts[1]:=f((tˆx)ˆy);
ts[2]:=ts[1]ˆf(y); ts[3]:=f(tˆ(x));
cst:= [null : i in [1 .. Index(G,sub<G|x,y>)]]
where null is[Integers() |];
for i := 1 to 4 do
cst[prodim(1, ts, [i])]:=[i];
end for;
m:=0; for i in [1..165] do if cst[i] ne []
then m:=m+1; end if; end for; m;
-----------------------------------------------------
N4:=Stabiliser(N,4);
Orbits(N4);
#N4;
-----------------------------------------------------
N01:=Stabiliser(N,[4,1]);
SS:={[4,1]};
SS:=SSˆN;
SS;
#SS;
Seqq:=Setseq(SS);
Seqq;
for i in [1..#SS] do
for n in IN do
if ts[4]
*
ts[1] eq
n
*
ts[Rep(Seqq[i])[1]]
*
ts[Rep(Seqq[i])[2]]
then print Rep(Seqq[i]);
end if; end for; end for;
N01; #N01;
T01:=Transversal(N,N01);
174
for i in [1..#T01] do
ss:=[4,1]ˆT01[i];
cst[prodim(1, ts, ss)]:=ss;
end for;
m:=0; for i in [1..165] do if cst[i] ne []
then m:=m+1; end if; end for; m;
Orbits(N01);
#N01;
-----------------------------------------------------
N412:=Stabiliser(N,[4,1,2]);
SSS:={[4,1,2]}; SSS:=SSSˆN;
SSS;
#(SSS);
Seqq:=Setseq(SSS);
Seqq;
for i in [1..#SSS] do
for n in IN do
if ts[4]
*
ts[1]
*
ts[2] eq
n
*
ts[Rep(Seqq[i])[1]]
*
ts[Rep(Seqq[i])[2]]
*
ts[Rep(Seqq[i])[3]]
then print Rep(Seqq[i]);
end if; end for; end for;
N012s:=N412;
T012:=Transversal(N,N012s);
for i in [1..#T012] do
ss:=[4,1,2]ˆT012[i];
cst[prodim(1, ts, ss)] := ss;
end for;
m:=0; for i in [1..165] do if cst[i] ne []
then m:=m+1; end if; end for; m;
Orbits(N012s);
#(N012s);
-----------------------------------------------------
N413:=Stabiliser(N,[4,1,3]);
SSS:={[4,1,3]}; SSS:=SSSˆN;
SSS;
#(SSS);
Seqq:=Setseq(SSS);
Seqq;
for i in [1..#SSS] do
for n in IN do
if ts[4]
*
ts[1]
*
ts[3] eq
n
*
ts[Rep(Seqq[i])[1]]
*
ts[Rep(Seqq[i])[2]]
*
ts[Rep(Seqq[i])[3]]
then print Rep(Seqq[i]);
end if; end for; end for;
175
N013s:=N413;
T013:=Transversal(N,N013s);
for i in [1..#T013] do
ss:=[4,1,3]ˆT013[i];
cst[prodim(1, ts, ss)] := ss;
end for;
m:=0; for i in [1..165] do if cst[i] ne []
then m:=m+1; end if; end for; m;
Orbits(N013s);
#N013s;
-----------------------------------------------------
N414:=Stabiliser(N,[4,1,4]);
SSS:={[4,1,4]}; SSS:=SSSˆN;
SSS;
#(SSS);
Seqq:=Setseq(SSS);
Seqq;
for i in [1..#SSS] do
for n in IN do
if ts[4]
*
ts[1]
*
ts[4] eq
n
*
ts[Rep(Seqq[i])[1]]
*
ts[Rep(Seqq[i])[2]]
*
ts[Rep(Seqq[i])[3]]
then print Rep(Seqq[i]);
end if; end for; end for;
N010s:=N414;
T010:=Transversal(N,N010s);
for i in [1..#T010] do
ss:=[4,1,4]ˆT010[i];
cst[prodim(1, ts, ss)] := ss;
end for;
m:=0; for i in [1..165] do if cst[i] ne []
then m:=m+1; end if; end for; m;
for g in IN do for h in IN do if ts[4]
*
ts[1]
*
ts[4] eq
g
*
(ts[4]
*
ts[1])ˆh
then g,h; break; end if; end for; end for;
for i in [1..12] do if ArrayP[i] eq N!(1,4)(2,3) then Sch[i];
end if; end for;
xxˆyy;
ts[4]
*
ts[1]
*
ts[4] eq f(xˆy)
*
ts[4]
*
ts[1];
-----------------------------------------------------
N4121:=Stabiliser(N,[4,1,2,1]);
SSSS:={[4,1,2,1]}; SSSS:=SSSSˆN;
SSSS;
#(SSSS);
Seqq:=Setseq(SSSS);
176
Seqq;
for i in [1..#SSSS] do
for n in IN do
if ts[4]
*
ts[1]
*
ts[2]
*
ts[1] eq
n
*
ts[Rep(Seqq[i])[1]]
*
ts[Rep(Seqq[i])[2]]
*
ts[Rep(Seqq[i])[3]]
*
ts[Rep(Seqq[i])[4]]
then print Rep(Seqq[i]);
end if; end for; end for;
N0121s:=N4121;
T0121:=Transversal(N,N0121s);
for i in [1..#T0121] do
ss:=[4,1,2,1]ˆT0121[i];
cst[prodim(1, ts, ss)] := ss;
end for;
m:=0; for i in [1..165] do if cst[i] ne []
then m:=m+1; end if; end for; m;
for g in IN do for h in IN do if ts[4]
*
ts[1]
*
ts[2]
*
ts[1] eq
g
*
(ts[4]
*
ts[1]
*
ts[3])ˆh
then g,h; break; end if; end for; end for;
for i in [1..12] do if ArrayP[i] eq N!(1,2)(3,4) then Sch[i];
end if; end for;
xx;
ts[4]
*
ts[1]
*
ts[2]
*
ts[1] eq f(x)
*
ts[3]
*
ts[1]
*
ts[2];
-----------------------------------------------------
N4124:=Stabiliser(N,[4,1,2,4]);
SSSS:={[4,1,2,4]}; SSSS:=SSSSˆN;
SSSS;
#SSSS;
Seqq:=Setseq(SSSS);
Seqq;
for i in [1..#SSSS] do
for n in IN do
if ts[4]
*
ts[1]
*
ts[2]
*
ts[4] eq
n
*
ts[Rep(Seqq[i])[1]]
*
ts[Rep(Seqq[i])[2]]
*
ts[Rep(Seqq[i])[3]]
*
ts[Rep(Seqq[i])[4]]
then print Rep(Seqq[i]);
end if; end for; end for;
N0124s:=N4124;
for n in N do if 4ˆn eq 2 and 1ˆn eq 3 and 2ˆn eq 4 then
N0124s:=sub<N|N0124s,n>; end if; end for;
N0124s; #N0124s;
T0124:=Transversal(N,N0124s);
for i in [1..#T0124] do
ss:=[4,1,2,4]ˆT0124[i];
177
cst[prodim(1, ts, ss)] := ss;
end for;
m:=0; for i in [1..165] do if cst[i] ne []
then m:=m+1; end if; end for; m;
Orbits(N0124s);
#N0124s;
-----------------------------------------------------
N4123:=Stabiliser(N,[4,1,2,3]);
SSSS:={[4,1,2,3]}; SSSS:=SSSSˆN;
SSSS;
#SSSS;
Seqq:=Setseq(SSSS);
Seqq;
for i in [1..#SSSS] do
for n in IN do
if ts[4]
*
ts[1]
*
ts[2]
*
ts[3] eq
n
*
ts[Rep(Seqq[i])[1]]
*
ts[Rep(Seqq[i])[2]]
*
ts[Rep(Seqq[i])[3]]
*
ts[Rep(Seqq[i])[4]]
then print Rep(Seqq[i]);
end if; end for; end for;
N0123s:=N4123;
T0123:=Transversal(N,N0123s);
for i in [1..#T0123] do
ss:=[4,1,2,3]ˆT0123[i];
cst[prodim(1, ts, ss)] := ss;
end for;
m:=0; for i in [1..165] do if cst[i] ne []
then m:=m+1; end if; end for; m;
Orbits(N0123s);
#N0123s;
-----------------------------------------------------
N4131:=Stabiliser(N,[4,1,3,1];
SSSS:={[4,1,3,1]}; SSSS:=SSSSˆN;
SSSS;
#SSSS;
Seqq:=Setseq(SSSS);
Seqq;
for i in [1..#SSSS] do
for n in IN do
if ts[4]
*
ts[1]
*
ts[3]
*
ts[1] eq
n
*
ts[Rep(Seqq[i])[1]]
*
ts[Rep(Seqq[i])[2]]
*
ts[Rep(Seqq[i])[3]]
*
ts[Rep(Seqq[i])[4]]
then print Rep(Seqq[i]);
end if; end for; end for;
178
N0131s:=N4131;
T0131:=Transversal(N,N0131s);
for i in [1..#T0131] do
ss:=[4,1,3,1]ˆT0131[i];
cst[prodim(1, ts, ss)] := ss;
end for;
m:=0; for i in [1..165] do if cst[i] ne []
then m:=m+1; end if; end for; m;
for g in IN do for h in IN do if ts[4]
*
ts[1]
*
ts[3]
*
ts[1] eq
g
*
(ts[4]
*
ts[1]
*
ts[2])ˆh then g,h; break; end if; end for;
end for;
for i in [1..12] do if ArrayP[i] eq N!(1,3)(2,4) then Sch[i];
end if; end for;
yy
*
xx
*
yyˆ-1;
ts[4]
*
ts[1]
*
ts[3]
*
ts[1] eq f(y
*
x
*
yˆ-1)
*
ts[2]
*
ts[1]
*
ts[3];
-----------------------------------------------------
N4134:=Stabiliser(N,[4,1,3,4];
SSSS:={[4,1,3,4]}; SSSS:=SSSSˆN;
SSSS;
#SSSS;
Seqq:=Setseq(SSSS);
Seqq;
for i in [1..#SSSS] do
for n in IN do
if ts[4]
*
ts[1]
*
ts[3]
*
ts[4] eq
n
*
ts[Rep(Seqq[i])[1]]
*
ts[Rep(Seqq[i])[2]]
*
ts[Rep(Seqq[i])[3]]
*
ts[Rep(Seqq[i])[4]]
then print Rep(Seqq[i]);
end if; end for; end for;
N0134s:=N4134;
for n in N do if 4ˆn eq 3 and 1ˆn eq 2 and 3ˆn eq 4 then
N0134s:=sub<N|N0134s,n>; end if; end for;
N0134s; #N0134s;
T0134:=Transversal(N,N0134s);
for i in [1..#T0134] do
ss:=[4,1,3,4]ˆT0134[i];
cst[prodim(1, ts, ss)] := ss;
end for;
m:=0; for i in [1..165] do if cst[i] ne []
then m:=m+1; end if; end for; m;
Stabiliser(N,[4,1,3,4]);
Orbits(N0134s);
#N0134s;
-----------------------------------------------------
179
N4132:=Stabiliser(N,[4,1,3,2]);
SSSS:={[4,1,3,2]}; SSSS:=SSSSˆN;
SSSS;
#SSSS;
Seqq:=Setseq(SSSS);
Seqq;
for i in [1..#SSSS] do
for n in IN do
if ts[4]
*
ts[1]
*
ts[3]
*
ts[2] eq
n
*
ts[Rep(Seqq[i])[1]]
*
ts[Rep(Seqq[i])[2]]
*
ts[Rep(Seqq[i])[3]]
*
ts[Rep(Seqq[i])[4]]
then print Rep(Seqq[i]);
end if; end for; end for;
N0132s:=N4132;
T0132:=Transversal(N,N0132s);
for i in [1..#T0132] do
ss:=[4,1,3,2]ˆT0132[i];
cst[prodim(1, ts, ss)] := ss;
end for;
m:=0; for i in [1..165] do if cst[i] ne []
then m:=m+1; end if; end for; m;
Stabiliser(N,[4,1,3,2]);
Orbits(N0132s);
#N0132s;
-----------------------------------------------------
N41241:=Stabiliser(N,[4,1,2,4,1]);
SSSSS:={[4,1,2,4,1]}; SSSSS:=SSSSSˆN;
SSSSS;
#SSSSS;
Seqq:=Setseq(SSSSS);
Seqq;
for i in [1..#SSSSS] do
for n in IN do
if ts[4]
*
ts[1]
*
ts[2]
*
ts[4]
*
ts[1] eq
n
*
ts[Rep(Seqq[i])[1]]
*
ts[Rep(Seqq[i])[2]]
*
ts[Rep(Seqq[i])[3]]
*
ts[Rep(Seqq[i])[4]]
*
ts[Rep(Seqq[i])[5]]
then print Rep(Seqq[i]);
end if; end for; end for;
N01241s:=N41241;
T01241:=Transversal(N,N01241s);
for i in [1..#T01241] do
ss:=[4,1,2,4,1]ˆT01241[i];
cst[prodim(1, ts, ss)] := ss;
end for;
180
m:=0; for i in [1..165] do if cst[i] ne []
then m:=m+1; end if; end for; m;
Orbits(N01241s);
#N01241s;
-----------------------------------------------------
N41232:=Stabiliser(N,[4,1,2,3,2]);
SSSSS:={[4,1,2,3,2]}; SSSSS:=SSSSSˆN;
SSSSS;
#SSSSS;
Seqq:=Setseq(SSSSS);
Seqq;
for i in [1..#SSSSS] do
for n in IN do
if ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[2] eq
n
*
ts[Rep(Seqq[i])[1]]
*
ts[Rep(Seqq[i])[2]]
*
ts[Rep(Seqq[i])[3]]
*
ts[Rep(Seqq[i])[4]]
*
ts[Rep(Seqq[i])[5]]
then print Rep(Seqq[i]);
end if; end for; end for;
N01232s:=N41232;
for n in N do if 4ˆn eq 1 and 1ˆn eq 3 and 3ˆn eq 4 then
N01232s:=sub<N| N01232s,n>; end if; end for;
for n in N do if 4ˆn eq 3 and 1ˆn eq 4 and 3ˆn eq 1 then
N01232s:=sub<N| N01232s,n>; end if; end for;
N01232s; #N01232s;
T01232:=Transversal(N,N01232s);
for i in [1..#T01232] do
ss:=[4,1,2,3,2]ˆT01232[i];
cst[prodim(1, ts, ss)] := ss;
end for;
m:=0; for i in [1..165] do if cst[i] ne []
then m:=m+1; end if; end for; m;
for g in IN do for h in IN do if ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[2]
eq g
*
(ts[4]
*
ts[1]
*
ts[3]
*
ts[2])ˆh
then g,h; break; end if; end for; end for;
for i in [1..12] do if ArrayP[i] eq N!(4,1)(2,3)then Sch[i];
end if; end for;
xxˆyy;
ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[2] eq
f(xˆy)
*
ts[1]
*
ts[4]
*
ts[2]
*
ts[3];
-----------------------------------------------------
N41234:=Stabiliser(N,[4,1,2,3,4]);
SSSSS:={[4,1,2,3,4]}; SSSSS:=SSSSSˆN;
SSSSS;
#SSSSS;
181
Seqq:=Setseq(SSSSS);
Seqq;
for i in [1..#SSSSS] do
for n in IN do
if ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[4] eq
n
*
ts[Rep(Seqq[i])[1]]
*
ts[Rep(Seqq[i])[2]]
*
ts[Rep(Seqq[i])[3]]
*
ts[Rep(Seqq[i])[4]]
*
ts[Rep(Seqq[i])[5]]
then print Rep(Seqq[i]);
end if; end for; end for;
N01234s:=N41234;
T01234:=Transversal(N,N01234s);
for i in [1..#T01234] do
ss:=[4,1,2,3,4]ˆT01234[i];
cst[prodim(1, ts, ss)] := ss;
end for;
m:=0; for i in [1..165] do if cst[i] ne []
then m:=m+1; end if; end for; m;
Orbits(N01234s);
#N01234s;
-----------------------------------------------------
N41231:=Stabiliser(N,[4,1,2,3,1]);
SSSSS:={[4,1,2,3,1]}; SSSSS:=SSSSSˆN;
SSSSS;
#SSSSS;
Seqq:=Setseq(SSSSS);
Seqq;
for i in [1..#SSSSS] do
for n in IN do
if ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[1] eq
n
*
ts[Rep(Seqq[i])[1]]
*
ts[Rep(Seqq[i])[2]]
*
ts[Rep(Seqq[i])[3]]
*
ts[Rep(Seqq[i])[4]]
*
ts[Rep(Seqq[i])[5]]
then print Rep(Seqq[i]);
end if; end for; end for;
N01231s:=N41231;
T01231:=Transversal(N,N01231s);
for i in [1..#T01231] do
ss:=[4,1,2,3,1]ˆT01231[i];
cst[prodim(1, ts, ss)] := ss;
end for;
m:=0; for i in [1..165] do if cst[i] ne []
then m:=m+1; end if; end for; m;
Orbits(N01231s);
#N01231s;
-----------------------------------------------------
182
N41341:=Stabiliser(N,[4,1,3,4,1]);
SSSSS:={[4,1,3,4,1]}; SSSSS:=SSSSSˆN;
SSSSS;
#SSSSS;
Seqq:=Setseq(SSSSS);
Seqq;
for i in [1..#SSSSS] do
for n in IN do
if ts[4]
*
ts[1]
*
ts[3]
*
ts[4]
*
ts[1] eq
n
*
ts[Rep(Seqq[i])[1]]
*
ts[Rep(Seqq[i])[2]]
*
ts[Rep(Seqq[i])[3]]
*
ts[Rep(Seqq[i])[4]]
*
ts[Rep(Seqq[i])[5]]
then print Rep(Seqq[i]);
end if; end for; end for;
N01341s:=N41341;
T01341:=Transversal(N,N01341s);
for i in [1..#T01341] do
ss:=[4,1,3,4,1]ˆT01341[i];
cst[prodim(1, ts, ss)] := ss;
end for;
m:=0; for i in [1..165] do if cst[i] ne []
then m:=m+1; end if; end for; m;
for g in IN do for h in IN do if ts[4]
*
ts[1]
*
ts[3]
*
ts[4]
*
ts[1]
eq g
*
(ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[1])ˆh
then g,h; break; end if; end for; end for;
for i in [1..12] do if ArrayP[i] eq N!(1,2)(3,4) then Sch[i];
end if; end for;
xx;
ts[4]
*
ts[1]
*
ts[3]
*
ts[4]
*
ts[1] eq
f(x)
*
ts[3]
*
ts[4]
*
ts[2]
*
ts[1]
*
ts[4];
-----------------------------------------------------
N41321:=Stabiliser(N,[4,1,3,2,1]);
SSSSS:={[4,1,3,2,1]}; SSSSS:=SSSSSˆN;
SSSSS;
#SSSSS;
Seqq:=Setseq(SSSSS);
Seqq;
for i in [1..#SSSSS] do
for n in IN do
if ts[4]
*
ts[1]
*
ts[3]
*
ts[2]
*
ts[1] eq
n
*
ts[Rep(Seqq[i])[1]]
*
ts[Rep(Seqq[i])[2]]
*
ts[Rep(Seqq[i])[3]]
*
ts[Rep(Seqq[i])[4]]
*
ts[Rep(Seqq[i])[5]]
then print Rep(Seqq[i]);
end if; end for; end for;
N01321s:=N41321;
183
T01321:=Transversal(N,N01321s);
for i in [1..#T01321] do
ss:=[4,1,3,2,1]ˆT01321[i];
cst[prodim(1, ts, ss)] := ss;
end for;
m:=0; for i in [1..165] do if cst[i] ne []
then m:=m+1; end if; end for; m;
for g in IN do for h in IN do if ts[4]
*
ts[1]
*
ts[3]
*
ts[2]
*
ts[1]
eq g
*
(ts[4]
*
ts[1]
*
ts[2]
*
ts[4]
*
ts[1])ˆh
then g,h; break; end if; end for; end for;
for i in [1..12] do if ArrayP[i] eq N!(1,4)(2,3) then Sch[i];
end if; end for;
xxˆyy;
ts[4]
*
ts[1]
*
ts[3]
*
ts[2]
*
ts[1] eq
f(xˆy)
*
ts[1]
*
ts[2]
*
ts[4]
*
ts[1]
*
ts[2];
-----------------------------------------------------
N41323:=Stabiliser(N,[4,1,3,2,3]);
SSSSS:={[4,1,3,2,3]}; SSSSS:=SSSSSˆN;
SSSSS;
#SSSSS;
Seqq:=Setseq(SSSSS);
Seqq;
for i in [1..#SSSSS] do
for n in IN do
if ts[4]
*
ts[1]
*
ts[3]
*
ts[2]
*
ts[3] eq
n
*
ts[Rep(Seqq[i])[1]]
*
ts[Rep(Seqq[i])[2]]
*
ts[Rep(Seqq[i])[3]]
*
ts[Rep(Seqq[i])[4]]
*
ts[Rep(Seqq[i])[5]]
then print Rep(Seqq[i]);
end if; end for; end for;
N01323s:=N41323;
for n in N do if 4ˆn eq 2 and 1ˆn eq 4 and 2ˆn eq 1 then
N01323s:=sub<N| N01323s,n>; end if; end for;
for n in N do if 4ˆn eq 1 and 1ˆn eq 2 and 2ˆn eq 4 then
N01323s:=sub<N| N01323s,n>; end if; end for;
N01323s; #N01323s;
T01323:=Transversal(N,N01323s);
for i in [1..#T01323] do
ss:=[4,1,3,2,3]ˆT01323[i];
cst[prodim(1, ts, ss)] := ss;
end for;
m:=0; for i in [1..165] do if cst[i] ne []
then m:=m+1; end if; end for; m;
for g in IN do for h in IN do if ts[4]
*
ts[1]
*
ts[3]
*
ts[2]
*
ts[3]
eq g
*
(ts[4]
*
ts[1]
*
ts[2]
*
ts[3])ˆh
184
then g,h; break; end if; end for; end for;
for i in [1..12] do if ArrayP[i] eq N!(1,4)(2,3) then Sch[i];
end if; end for;
xxˆyy;
ts[4]
*
ts[1]
*
ts[3]
*
ts[2]
*
ts[3] eq
f(xˆy)
*
ts[1]
*
ts[4]
*
ts[3]
*
ts[2];
-----------------------------------------------------
N41324:=Stabiliser(N,[4,1,3,2,4]);
SSSSS:={[4,1,3,2,4]}; SSSSS:=SSSSSˆN;
SSSSS;
#SSSSS;
Seqq:=Setseq(SSSSS);
Seqq;
for i in [1..#SSSSS] do
for n in IN do
if ts[4]
*
ts[1]
*
ts[3]
*
ts[2]
*
ts[4] eq
n
*
ts[Rep(Seqq[i])[1]]
*
ts[Rep(Seqq[i])[2]]
*
ts[Rep(Seqq[i])[3]]
*
ts[Rep(Seqq[i])[4]]
*
ts[Rep(Seqq[i])[5]]
then print Rep(Seqq[i]);
end if; end for; end for;
N01324s:=N41324;
T01324:=Transversal(N,N01324s);
for i in [1..#T01324] do
ss:=[4,1,3,2,4]ˆT01324[i];
cst[prodim(1, ts, ss)] := ss;
end for;
m:=0; for i in [1..165] do if cst[i] ne []
then m:=m+1; end if; end for; m;
Orbits(N01324s);
#N01324s;
-----------------------------------------------------
N412412:=Stabiliser(N,[4,1,2,4,1,2]);
SSSSSS:={[4,1,2,4,1,2]}; SSSSSS:=SSSSSSˆN;
SSSSSS;
#SSSSSS;
Seqq:=Setseq(SSSSSS);
Seqq;
for i in [1..#SSSSSS] do
for n in IN do
if ts[4]
*
ts[1]
*
ts[2]
*
ts[4]
*
ts[1]
*
ts[2] eq
n
*
ts[Rep(Seqq[i])[1]]
*
ts[Rep(Seqq[i])[2]]
*
ts[Rep(Seqq[i])[3]]
*
ts[Rep(Seqq[i])[4]]
*
ts[Rep(Seqq[i])[5]]
*
ts[Rep(Seqq[i])[6]]
then print Rep(Seqq[i]);
end if; end for; end for;
185
N012412s:=N412412;
T012412:=Transversal(N,N012412s);
for i in [1..#T012412] do
ss:=[4,1,2,4,1,2]ˆT012412[i];
cst[prodim(1, ts, ss)] := ss;
end for;
m:=0; for i in [1..165] do if cst[i] ne []
then m:=m+1; end if; end for; m;
for g in IN do for h in IN do if
ts[4]
*
ts[1]
*
ts[2]
*
ts[4]
*
ts[1]
*
ts[2] eq
g
*
(ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[4])ˆh
then g,h; break; end if; end for; end for;
for i in [1..12] do if ArrayP[i] eq N!Id(N) then Sch[i];
end if; end for;
xxˆyy;
ts[4]
*
ts[1]
*
ts[2]
*
ts[4]
*
ts[1]
*
ts[2] eq
ts[1]
*
ts[4]
*
ts[3]
*
ts[2]
*
ts[1];
-----------------------------------------------------
N412413:=Stabiliser(N,[4,1,2,4,1,3]);
SSSSSS:={[4,1,2,4,1,3]}; SSSSSS:=SSSSSSˆN;
SSSSSS;
#SSSSSS;
Seqq:=Setseq(SSSSSS);
Seqq;
for i in [1..#SSSSSS] do
for n in IN do
if ts[4]
*
ts[1]
*
ts[2]
*
ts[4]
*
ts[1]
*
ts[3] eq
n
*
ts[Rep(Seqq[i])[1]]
*
ts[Rep(Seqq[i])[2]]
*
ts[Rep(Seqq[i])[3]]
*
ts[Rep(Seqq[i])[4]]
*
ts[Rep(Seqq[i])[5]]
*
ts[Rep(Seqq[i])[6]]
then print Rep(Seqq[i]);
end if; end for; end for;
N012413s:=N412413;
T012413:=Transversal(N,N012413s);
for i in [1..#T012413] do
ss:=[4,1,2,4,1,3]ˆT012413[i];
cst[prodim(1, ts, ss)] := ss;
end for;
m:=0; for i in [1..165] do if cst[i] ne []
then m:=m+1; end if; end for; m;
Orbits(N012413s);
#N012413s;
-----------------------------------------------------
for i in [1..4] do for g in IN do for h in IN do if
ts[4]
*
ts[1]
*
ts[2]
*
ts[4]
*
ts[1]
*
ts[i] eq
186
g
*
(ts[4]
*
ts[1]
*
ts[3]
*
ts[2])ˆh
then i; break; end if; end for; end for;end for;
for g in IN do for h in IN do if
ts[4]
*
ts[1]
*
ts[2]
*
ts[4]
*
ts[1]
*
ts[4]
eq g
*
(ts[4]
*
ts[1]
*
ts[3]
*
ts[2])ˆh
then g,h; break; end if; end for; end for;
for i in [1..12] do if ArrayP[i] eq N!(1,3)(2,4) then Sch[i];
end if; end for;
yy
*
xx
*
yyˆ-1;
ts[4]
*
ts[1]
*
ts[2]
*
ts[4]
*
ts[1]
*
ts[4] eq
f(y
*
x
*
yˆ-1)
*
ts[2]
*
ts[4]
*
ts[3]
*
ts[1];
-----------------------------------------------------
N412341:=Stabiliser(N,[4,1,2,3,4,1]);
SSSSSS:={[4,1,2,3,4,1]}; SSSSSS:=SSSSSSˆN;
SSSSSS;
#SSSSSS;
Seqq:=Setseq(SSSSSS);
Seqq;
for i in [1..#SSSSSS] do
for n in IN do
if ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[4]
*
ts[1] eq
n
*
ts[Rep(Seqq[i])[1]]
*
ts[Rep(Seqq[i])[2]]
*
ts[Rep(Seqq[i])[3]]
*
ts[Rep(Seqq[i])[4]]
*
ts[Rep(Seqq[i])[5]]
*
ts[Rep(Seqq[i])[6]]
then print Rep(Seqq[i]);
end if; end for; end for;
N012341s:=N412341;
for n in N do if 4ˆn eq 3 and 1ˆn eq 2 and 2ˆn eq 1 and 3ˆn
eq 4 then N012341s:=sub<N|N012341s,n>; end if; end for;
N012341s; #N012341s;
T012341:=Transversal(N,N012341s);
for i in [1..#T012341] do
ss:=[4,1,2,3,4,1]ˆT012341[i];
cst[prodim(1, ts, ss)] := ss;
end for;
m:=0; for i in [1..165] do if cst[i] ne []
then m:=m+1; end if; end for; m;
Orbits(N012341s);
#N012341s;
-----------------------------------------------------
N412342:=Stabiliser(N,[4,1,2,3,4,2]);
SSSSSS:={[4,1,2,3,4,2]}; SSSSSS:=SSSSSSˆN;
SSSSSS;
#SSSSSS;
Seqq:=Setseq(SSSSSS);
187
Seqq;
for i in [1..#SSSSSS] do
for n in IN do
if ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[4]
*
ts[2] eq
n
*
ts[Rep(Seqq[i])[1]]
*
ts[Rep(Seqq[i])[2]]
*
ts[Rep(Seqq[i])[3]]
*
ts[Rep(Seqq[i])[4]]
*
ts[Rep(Seqq[i])[5]]
*
ts[Rep(Seqq[i])[6]]
then print Rep(Seqq[i]);
end if; end for; end for;
N012342s:=N412342;
T012342:=Transversal(N,N012342s);
for i in [1..#T012342] do
ss:=[4,1,2,3,4,2]ˆT012342[i];
cst[prodim(1, ts, ss)] := ss;
end for;
m:=0; for i in [1..165] do if cst[i] ne []
then m:=m+1; end if; end for; m;
for g in IN do for h in IN do if
ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[4]
*
ts[2]
eq g
*
(ts[4]
*
ts[1]
*
ts[2]
*
ts[4]
*
ts[1]
*
ts[3])ˆh
then g,h; break; end if; end for; end for;
for i in [1..12] do if ArrayP[i] eq N!(2,4)(1,3) then Sch[i];
end if; end for;
yy
*
xx
*
yyˆ-1;
ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[4]
*
ts[2] eq
f(y
*
x
*
yˆ-1)
*
ts[2]
*
ts[1]
*
ts[3]
*
ts[2]
*
ts[1]
*
ts[4];
-----------------------------------------------------
for i in [1..4] do for g in IN do for h in IN do if
ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[4]
*
ts[i] eq
g
*
(ts[4]
*
ts[1]
*
ts[2]
*
ts[4]
*
ts[1])ˆh
then i; break; end if; end for; end for;end for;
for g in IN do for h in IN do if
ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[4]
*
ts[3]
eq g
*
(ts[4]
*
ts[1]
*
ts[2]
*
ts[4]
*
ts[1])ˆh
then g,h; break; end if; end for; end for;
for i in [1..12] do if ArrayP[i] eq N!Id(N) then Sch[i];
end if; end for;
ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[4]
*
ts[3] eq
ts[1]
*
ts[4]
*
ts[3]
*
ts[1]
*
ts[4];
-----------------------------------------------------
N412312:=Stabiliser(N,[4,1,2,3,1,2]);
SSSSSS:={[4,1,2,3,1,2]}; SSSSSS:=SSSSSSˆN;
SSSSSS;
#SSSSSS;
Seqq:=Setseq(SSSSSS);
188
Seqq;
for i in [1..#SSSSSS] do
for n in IN do
if ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[1]
*
ts[2] eq
n
*
ts[Rep(Seqq[i])[1]]
*
ts[Rep(Seqq[i])[2]]
*
ts[Rep(Seqq[i])[3]]
*
ts[Rep(Seqq[i])[4]]
*
ts[Rep(Seqq[i])[5]]
*
ts[Rep(Seqq[i])[6]]
then print Rep(Seqq[i]);
end if; end for; end for;
N012312s:=N412312;
T012312:=Transversal(N,N012312s);
for i in [1..#T012312] do
ss:=[4,1,2,3,1,2]ˆT012312[i];
cst[prodim(1, ts, ss)] := ss;
end for;
m:=0; for i in [1..165] do if cst[i] ne []
then m:=m+1; end if; end for; m;
Orbits(N012312s);
#N012312s;
-----------------------------------------------------
for i in [1..4] do for g in IN do for h in IN do if
ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[1]
*
ts[i] eq
g
*
(ts[4]
*
ts[1]
*
ts[3]
*
ts[4])ˆh
then i; break; end if; end for; end for;end for;
for g in IN do for h in IN do if
ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[1]
*
ts[3]
eq g
*
(ts[4]
*
ts[1]
*
ts[3]
*
ts[4])ˆh
then g,h; break; end if; end for; end for;
for i in [1..12] do if ArrayP[i] eq N!(1,3)(2,4) then Sch[i];
end if; end for;
yy
*
xx
*
yyˆ-1;
ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[1]
*
ts[3] eq
f(y
*
x
*
yˆ-1)
*
ts[4]
*
ts[2]
*
ts[1]
*
ts[4];
-----------------------------------------------------
N412314:=Stabiliser(N,[4,1,2,3,1,4]);
SSSSSS:={[4,1,2,3,1,4]}; SSSSSS:=SSSSSSˆN;
SSSSSS;
#SSSSSS;
Seqq:=Setseq(SSSSSS);
Seqq;
for i in [1..#SSSSSS] do
for n in IN do
if ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[1]
*
ts[4] eq
n
*
ts[Rep(Seqq[i])[1]]
*
ts[Rep(Seqq[i])[2]]
*
ts[Rep(Seqq[i])[3]]
*
ts[Rep(Seqq[i])[4]]
*
ts[Rep(Seqq[i])[5]]
*
ts[Rep(Seqq[i])[6]]
189
then print Rep(Seqq[i]);
end if; end for; end for;
N012314s:=N412314;
T012314:=Transversal(N,N012314s);
for i in [1..#T012314] do
ss:=[4,1,2,3,1,4]ˆT012314[i];
cst[prodim(1, ts, ss)] := ss;
end for;
m:=0; for i in [1..165] do if cst[i] ne []
then m:=m+1; end if; end for; m;
for g in IN do for h in IN do if
ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[1]
*
ts[4]
eq g
*
(ts[4]
*
ts[1]
*
ts[3]
*
ts[2]
*
ts[4])ˆh
then g,h; break; end if; end for; end for;
for i in [1..12] do if ArrayP[i] eq N!(1,4)(2,3) then Sch[i];
end if; end for;
xxˆyy;
ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[1]
*
ts[4] eq
f(xˆy)
*
ts[3]
*
ts[1]
*
ts[2]
*
ts[4]
*
ts[3];
-----------------------------------------------------
N413241:=Stabiliser(N,[4,1,3,2,4,1]);
SSSSSS:={[4,1,3,2,4,1]}; SSSSSS:=SSSSSSˆN;
SSSSSS;
#SSSSSS;
Seqq:=Setseq(SSSSSS);
Seqq;
for i in [1..#SSSSSS] do
for n in IN do
if ts[4]
*
ts[1]
*
ts[3]
*
ts[2]
*
ts[4]
*
ts[1] eq
n
*
ts[Rep(Seqq[i])[1]]
*
ts[Rep(Seqq[i])[2]]
*
ts[Rep(Seqq[i])[3]]
*
ts[Rep(Seqq[i])[4]]
*
ts[Rep(Seqq[i])[5]]
*
ts[Rep(Seqq[i])[6]]
then print Rep(Seqq[i]);
end if; end for; end for;
N013241s:=N413241;
for n in N do if 4ˆn eq 2 and 1ˆn eq 3 and 2ˆn eq 4 and 3ˆn
eq 1 then N013241s:=sub<N|N013241s,n>; end if; end for;
N013241s; #N013241s;
T013241:=Transversal(N,N013241s);
for i in [1..#T013241] do
ss:=[4,1,3,2,4,1]ˆT013241[i];
cst[prodim(1, ts, ss)] := ss;
end for;
m:=0; for i in [1..165] do if cst[i] ne []
then m:=m+1; end if; end for; m;
190
for g in IN do for h in IN do if
ts[4]
*
ts[1]
*
ts[3]
*
ts[2]
*
ts[4]
*
ts[1]
eq g
*
(ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[4]
*
ts[1])ˆh
then g,h; break; end if; end for; end for;
for i in [1..12] do if ArrayP[i] eq N!Id(N) then Sch[i];
end if; end for;
ts[4]
*
ts[1]
*
ts[3]
*
ts[2]
*
ts[4]
*
ts[1] eq
ts[1]
*
ts[2]
*
ts[4]
*
ts[3]
*
ts[1]
*
ts[2];
-----------------------------------------------------
for i in [1..4] do for g in IN do for h in IN do if
ts[4]
*
ts[1]
*
ts[3]
*
ts[2]
*
ts[4]
*
ts[i] eq
g
*
(ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[1])ˆh
then i; break; end if; end for; end for;end for;
for g in IN do for h in IN do if
ts[4]
*
ts[1]
*
ts[3]
*
ts[2]
*
ts[4]
*
ts[2]
eq g
*
(ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[1])ˆh
then g,h; break; end if; end for; end for;
for i in [1..12] do if ArrayP[i] eq N!(1,2)(3,4) then Sch[i];
end if; end for;
xx;
ts[4]
*
ts[1]
*
ts[3]
*
ts[2]
*
ts[4]
*
ts[2] eq
f(x)
*
ts[2]
*
ts[1]
*
ts[3]
*
ts[4]
*
ts[1];
-----------------------------------------------------
N413243:=Stabiliser(N,[4,1,3,2,4,3]);
SSSSSS:={[4,1,3,2,4,3]}; SSSSSS:=SSSSSSˆN;
SSSSSS;
#SSSSSS;
Seqq:=Setseq(SSSSSS);
Seqq;
for i in [1..#SSSSSS] do
for n in IN do
if ts[4]
*
ts[1]
*
ts[3]
*
ts[2]
*
ts[4]
*
ts[3] eq
n
*
ts[Rep(Seqq[i])[1]]
*
ts[Rep(Seqq[i])[2]]
*
ts[Rep(Seqq[i])[3]]
*
ts[Rep(Seqq[i])[4]]
*
ts[Rep(Seqq[i])[5]]
*
ts[Rep(Seqq[i])[6]]
then print Rep(Seqq[i]);
end if; end for; end for;
N013243s:=N413243;
T013243:=Transversal(N,N013243s);
for i in [1..#T013243] do
ss:=[4,1,3,2,4,3]ˆT013243[i];
cst[prodim(1, ts, ss)] := ss;
end for;
m:=0; for i in [1..165] do if cst[i] ne []
then m:=m+1; end if; end for; m;
191
for g in IN do for h in IN do if
ts[4]
*
ts[1]
*
ts[3]
*
ts[2]
*
ts[4]
*
ts[3]
eq g
*
(ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[1]
*
ts[2])ˆh
then g,h; break; end if; end for; end for;
for i in [1..12] do if ArrayP[i] eq N!(2,4)(1,3) then Sch[i];
end if; end for;
yy
*
xx
*
yyˆ-1;
ts[4]
*
ts[1]
*
ts[3]
*
ts[2]
*
ts[4]
*
ts[3] eq
f(y
*
x
*
yˆ-1)
*
ts[2]
*
ts[3]
*
ts[4]
*
ts[1]
*
ts[3]
*
ts[4];
-----------------------------------------------------
N4124131:=Stabiliser(N,[4,1,2,4,1,3,1]);
SSSSSSS:={[4,1,2,4,1,3,1]}; SSSSSSS:=SSSSSSSˆN;
SSSSSSS;
#SSSSSSS;
Seqq:=Setseq(SSSSSSS);
Seqq;
for i in [1..#SSSSSSS] do
for n in IN do
if ts[4]
*
ts[1]
*
ts[2]
*
ts[4]
*
ts[1]
*
ts[3]
*
ts[1] eq
n
*
ts[Rep(Seqq[i])[1]]
*
ts[Rep(Seqq[i])[2]]
*
ts[Rep(Seqq[i])[3]]
*
ts[Rep(Seqq[i])[4]]
*
ts[Rep(Seqq[i])[5]]
*
ts[Rep(Seqq[i])[6]]
*
ts[Rep(Seqq[i])[7]]
then print Rep(Seqq[i]);
end if; end for; end for;
N0120131s:=N4124131;
T0120131:=Transversal(N,N0120131s);
for i in [1..#T0120131] do
ss:=[4,1,2,4,1,3,1]ˆT0120131[i];
cst[prodim(1, ts, ss)] := ss;
end for;
m:=0; for i in [1..165] do if cst[i] ne []
then m:=m+1; end if; end for; m;
for g in IN do for h in IN do if
ts[4]
*
ts[1]
*
ts[2]
*
ts[4]
*
ts[1]
*
ts[3]
*
ts[1]
eq g
*
(ts[4]
*
ts[1]
*
ts[2]
*
ts[4]
*
ts[1]
*
ts[3])ˆh
then g,h; break; end if; end for; end for;
for i in [1..12] do if ArrayP[i] eq N!(1,4)(2,3) then Sch[i];
end if; end for;
xxˆyy;
ts[4]
*
ts[1]
*
ts[2]
*
ts[4]
*
ts[1]
*
ts[3]
*
ts[1] eq
f(xˆy)
*
ts[4]
*
ts[1]
*
ts[2]
*
ts[4]
*
ts[1]
*
ts[3];
-----------------------------------------------------
N4124132:=Stabiliser(N,[4,1,2,4,1,3,2]);
SSSSSSS:={[4,1,2,4,1,3,2]}; SSSSSSS:=SSSSSSSˆN;
192
SSSSSSS;
#SSSSSSS;
Seqq:=Setseq(SSSSSSS);
Seqq;
for i in [1..#SSSSSSS] do
for n in IN do
if ts[4]
*
ts[1]
*
ts[2]
*
ts[4]
*
ts[1]
*
ts[3]
*
ts[2] eq
n
*
ts[Rep(Seqq[i])[1]]
*
ts[Rep(Seqq[i])[2]]
*
ts[Rep(Seqq[i])[3]]
*
ts[Rep(Seqq[i])[4]]
*
ts[Rep(Seqq[i])[5]]
*
ts[Rep(Seqq[i])[6]]
*
ts[Rep(Seqq[i])[7]]
then print Rep(Seqq[i]);
end if; end for; end for;
N0120132s:=N4124132;
for n in N do if 4ˆn eq 2 and 1ˆn eq 1 and 2ˆn eq 3 and 3ˆn
eq 4 then N0120132s:=sub<N|N0120132s,n>; end if; end for;
N0120132s; #N4124132;
N0120132s:=N4124132;
for n in N do if 4ˆn eq 3 and 1ˆn eq 1 and 2ˆn eq 4 and 3ˆn
eq 2 then N0120132s:=sub<N|N0120132s,n>; end if; end for;
N0120132s; #N4124132;
T0120132:=Transversal(N,N0120132s);
for i in [1..#T0120132] do
ss:=[4,1,2,4,1,3,2]ˆT0120132[i];
cst[prodim(1, ts, ss)] := ss;
end for;
m:=0; for i in [1..165] do if cst[i] ne []
then m:=m+1; end if; end for; m;
N0120132s; #N0120132s;
Orbits(N0120132s);
-----------------------------------------------------
N4124134:=Stabiliser(N,[4,1,2,4,1,3,4]);
SSSSSSS:={[4,1,2,4,1,3,4]}; SSSSSSS:=SSSSSSSˆN;
SSSSSSS;
#SSSSSSS;
Seqq:=Setseq(SSSSSSS);
Seqq;
for i in [1..#SSSSSSS] do
for n in IN do
if ts[4]
*
ts[1]
*
ts[2]
*
ts[4]
*
ts[1]
*
ts[3]
*
ts[4] eq
n
*
ts[Rep(Seqq[i])[1]]
*
ts[Rep(Seqq[i])[2]]
*
ts[Rep(Seqq[i])[3]]
*
ts[Rep(Seqq[i])[4]]
*
ts[Rep(Seqq[i])[5]]
*
ts[Rep(Seqq[i])[6]]
*
ts[Rep(Seqq[i])[7]]
then print Rep(Seqq[i]);
end if; end for; end for;
193
N0124134s:=N4124134;
T0124134:=Transversal(N,N0124134s);
for i in [1..#T0124134] do
ss:=[4,1,2,4,1,3,4]ˆT0124134[i];
cst[prodim(1, ts, ss)] := ss;
end for;
m:=0; for i in [1..165] do if cst[i] ne []
then m:=m+1; end if; end for; m;
for g in IN do for h in IN do if
ts[4]
*
ts[1]
*
ts[2]
*
ts[4]
*
ts[1]
*
ts[3]
*
ts[4]
eq g
*
(ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[4])ˆh
then g,h; break; end if; end for; end for;
for i in [1..12] do if ArrayP[i] eq N!(1,2)(3,4) then Sch[i];
end if; end for;
xx;
ts[4]
*
ts[1]
*
ts[2]
*
ts[4]
*
ts[1]
*
ts[3]
*
ts[4] eq
f(x)
*
ts[3]
*
ts[1]
*
ts[4]
*
ts[2]
*
ts[3];
-----------------------------------------------------
for i in [1..4] do for g in IN do for h in IN do if
ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[4]
*
ts[1]
*
ts[i] eq
g
*
(ts[4]
*
ts[1]
*
ts[3]
*
ts[2]
*
ts[4])ˆh
then i; break; end if; end for; end for;end for;
for g in IN do for h in IN do if
ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[4]
*
ts[1]
*
ts[3]
eq g
*
(ts[4]
*
ts[1]
*
ts[3]
*
ts[2]
*
ts[4])ˆh
then g,h; break; end if; end for; end for;
for i in [1..12] do if ArrayP[i] eq N!Id(N) then Sch[i];
end if; end for;
ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[4]
*
ts[1]
*
ts[3] eq
ts[1]
*
ts[3]
*
ts[4]
*
ts[2]
*
ts[1];
-----------------------------------------------------
for g in IN do for h in IN do if
ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[4]
*
ts[1]
*
ts[4]
eq g
*
(ts[4]
*
ts[1]
*
ts[3]
*
ts[2]
*
ts[4])ˆh
then g,h; break; end if; end for; end for;
for i in [1..12] do if ArrayP[i] eq N!Id(N) then Sch[i];
end if; end for;
ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[4]
*
ts[1]
*
ts[4] eq
ts[2]
*
ts[4]
*
ts[3]
*
ts[1]
*
ts[2];
-----------------------------------------------------
for i in [1..4] do for g in IN do for h in IN do if
ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[1]
*
ts[2]
*
ts[i] eq
g
*
(ts[4]
*
ts[1]
*
ts[3]
*
ts[2]
*
ts[4])ˆh
then i; break; end if; end for; end for;end for;
194
for g in IN do for h in IN do if
ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[1]
*
ts[2]
*
ts[1]
eq g
*
(ts[4]
*
ts[1]
*
ts[3]
*
ts[2]
*
ts[4])ˆh
then g,h; break; end if; end for; end for;
for i in [1..12] do if ArrayP[i] eq N!(1,3)(2,4) then Sch[i];
end if; end for;
yy
*
xx
*
yyˆ-1;
ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[1]
*
ts[2]
*
ts[1] eq
f(y
*
x
*
yˆ-1)
*
ts[2]
*
ts[3]
*
ts[1]
*
ts[4]
*
ts[2];
-----------------------------------------------------
N4123123:=Stabiliser(N,[4,1,2,3,1,2,3]);
SSSSSSS:={[4,1,2,3,1,2,3]}; SSSSSSS:=SSSSSSSˆN;
SSSSSSS;
#SSSSSSS;
Seqq:=Setseq(SSSSSSS);
Seqq;
for i in [1..#SSSSSSS] do
for n in IN do
if ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[1]
*
ts[2]
*
ts[3] eq
n
*
ts[Rep(Seqq[i])[1]]
*
ts[Rep(Seqq[i])[2]]
*
ts[Rep(Seqq[i])[3]]
*
ts[Rep(Seqq[i])[4]]
*
ts[Rep(Seqq[i])[5]]
*
ts[Rep(Seqq[i])[6]]
*
ts[Rep(Seqq[i])[7]]
then print Rep(Seqq[i]);
end if; end for; end for;
N0123123s:=N4123123;
T0123123:=Transversal(N,N0123123s);
for i in [1..#T0123123] do
ss:=[4,1,2,3,1,2,3]ˆT0123123[i];
cst[prodim(1, ts, ss)] := ss;
end for;
m:=0; for i in [1..165] do if cst[i] ne []
then m:=m+1; end if; end for; m;
for g in IN do for h in IN do if
ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[1]
*
ts[2]
*
ts[3]
eq g
*
(ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[1]
*
ts[2])ˆh
then g,h; break; end if; end for; end for;
for i in [1..12] do if ArrayP[i] eq N!(2,4)(1,3) then Sch[i];
end if; end for;
yy
*
xx
*
yyˆ-1;
ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[1]
*
ts[2]
*
ts[3] eq
f(y
*
x
*
yˆ-1)
*
ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[1]
*
ts[2];
-----------------------------------------------------
N4123124:=Stabiliser(N,[4,1,2,3,1,2,4]);
SSSSSSS:={[4,1,2,3,1,2,4]}; SSSSSSS:=SSSSSSSˆN;
195
SSSSSSS;
#SSSSSSS;
Seqq:=Setseq(SSSSSSS);
Seqq;
for i in [1..#SSSSSSS] do
for n in IN do
if ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[1]
*
ts[2]
*
ts[4] eq
n
*
ts[Rep(Seqq[i])[1]]
*
ts[Rep(Seqq[i])[2]]
*
ts[Rep(Seqq[i])[3]]
*
ts[Rep(Seqq[i])[4]]
*
ts[Rep(Seqq[i])[5]]
*
ts[Rep(Seqq[i])[6]]
*
ts[Rep(Seqq[i])[7]]
then print Rep(Seqq[i]);
end if; end for; end for;
N0123124s:=N4123124;
for n in N do if 4ˆn eq 2 and 1ˆn eq 4 and 2ˆn eq 1 and 3ˆn
eq 3 then N0123124s:=sub<N|N0123124s,n>; end if; end for;
N0123124s:=N4123124;
for n in N do if 4ˆn eq 1 and 1ˆn eq 2 and 2ˆn eq 4 and 3ˆn
eq 3 then N0123124s:=sub<N|N0123124s,n>; end if; end for;
N0123124s; #N0123124s;
T0123124:=Transversal(N,N0123124s);
for i in [1..#T0123124] do
ss:=[4,1,2,3,1,2,4]ˆT0123124[i];
cst[prodim(1, ts, ss)] := ss;
end for;
m:=0; for i in [1..165] do if cst[i] ne []
then m:=m+1; end if; end for; m;
Orbits(N0123124s);
#N0123124s;
-----------------------------------------------------
N41241321:=Stabiliser(N,[4,1,2,4,1,3,2,1]);
SSSSSSSS:={[4,1,2,4,1,3,2,1]}; SSSSSSSS:=SSSSSSSSˆN;
SSSSSSSS;
#SSSSSSSS;
Seqq:=Setseq(SSSSSSSS);
Seqq;
for i in [1..#SSSSSSSS] do
for n in IN do
if ts[4]
*
ts[1]
*
ts[2]
*
ts[4]
*
ts[1]
*
ts[3]
*
ts[2]
*
ts[1] eq
n
*
ts[Rep(Seqq[i])[1]]
*
ts[Rep(Seqq[i])[2]]
*
ts[Rep(Seqq[i])[3]]
*
ts[Rep(Seqq[i])[4]]
*
ts[Rep(Seqq[i])[5]]
*
ts[Rep(Seqq[i])[6]]
*
ts[Rep(Seqq[i])[7]]
*
ts[Rep(Seqq[i])[8]]
then print Rep(Seqq[i]);
end if; end for; end for;
N01241321s:=N41241321;
196
for n in N do if 4ˆn eq 2 and 1ˆn eq 4 and 2ˆn eq 1 and 3ˆn
eq 3 then N01241321s:=sub<N|N01241321s,n>; end if; end for;
N01241321s; #N01241321s;
for n in N do if 4ˆn eq 4 and 1ˆn eq 3 and 2ˆn eq 1 and 3ˆn
eq 2 then N01241321s:=sub<N|N01241321s,n>; end if; end for;
N01241321s; #N01241321s;
T01241321:=Transversal(N,N01241321s);
for i in [1..#T01241321] do
ss:=[4,1,2,4,1,3,2,1]ˆT01241321[i];
cst[prodim(1, ts, ss)] := ss;
end for;
m:=0; for i in [1..165] do if cst[i] ne []
then m:=m+1; end if; end for; m;
Orbits(N01241321s);
-----------------------------------------------------
N41231241:=Stabiliser(N,[4,1,2,3,1,2,4,1]);
SSSSSSSS:={[4,1,2,3,1,2,4,1]}; SSSSSSSS:=SSSSSSSSˆN;
SSSSSSSS;
#SSSSSSSS;
Seqq:=Setseq(SSSSSSSS);
Seqq;
for i in [1..#SSSSSSSS] do
for n in IN do
if ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[1]
*
ts[2]
*
ts[4]
*
ts[1] eq
n
*
ts[Rep(Seqq[i])[1]]
*
ts[Rep(Seqq[i])[2]]
*
ts[Rep(Seqq[i])[3]]
*
ts[Rep(Seqq[i])[4]]
*
ts[Rep(Seqq[i])[5]]
*
ts[Rep(Seqq[i])[6]]
*
ts[Rep(Seqq[i])[7]]
*
ts[Rep(Seqq[i])[8]]
then print Rep(Seqq[i]); end if; end for; end for;
N01231241s:=N41231241;
T01231241:=Transversal(N,N01231241s);
for i in [1..#T01231241] do
ss:=[4,1,2,3,1,2,4,1]ˆT01231241[i];
cst[prodim(1, ts, ss)] := ss;
end for;
m:=0; for i in [1..165] do if cst[i] ne []
then m:=m+1; end if; end for; m;
for g in IN do for h in IN do if
ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[1]
*
ts[2]
*
ts[4]
*
ts[1] eq
g
*
(ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[1]
*
ts[2])ˆh
then g,h; break; end if; end for; end for;
for i in [1..12] do if ArrayP[i] eq N!Id(N) then Sch[i];
end if; end for;
ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[1]
*
ts[2]
*
ts[4]
*
ts[1] eq
ts[1]
*
ts[2]
*
ts[4]
*
ts[3]
*
ts[2]
*
ts[4];
197
-----------------------------------------------------
N41231243:=Stabiliser(N,[4,1,2,3,1,2,4,3]);
SSSSSSSS:={[4,1,2,3,1,2,4,3]}; SSSSSSSS:=SSSSSSSSˆN;
SSSSSSSS;
#SSSSSSSS;
Seqq:=Setseq(SSSSSSSS);
Seqq;
for i in [1..#SSSSSSSS] do
for n in IN do
if ts[4]
*
ts[1]
*
ts[2]
*
ts[3]
*
ts[1]
*
ts[2]
*
ts[4]
*
ts[3] eq
n
*
ts[Rep(Seqq[i])[1]]
*
ts[Rep(Seqq[i])[2]]
*
ts[Rep(Seqq[i])[3]]
*
ts[Rep(Seqq[i])[4]]
*
ts[Rep(Seqq[i])[5]]
*
ts[Rep(Seqq[i])[6]]
*
ts[Rep(Seqq[i])[7]]
*
ts[Rep(Seqq[i])[8]]
then print Rep(Seqq[i]);
end if; end for; end for;
N01231243s:=N41231243;
for n in N do if 4ˆn eq 4 and 1ˆn eq 3 and 2ˆn eq 1 and 3ˆn
eq 2 then N01231243s:=sub<N|N01231243s,n>; end if; end for;
N01231243s; #N01231243s;
for n in N do if 4ˆn eq 2 and 1ˆn eq 4 and 2ˆn eq 1 and 3ˆn
eq 3 then N01231243s:=sub<N|N01231243s,n>; end if; end for;
N01231243s; #N01231243s;
T01231243:=Transversal(N,N01231243s);
for i in [1..#T01231243] do
ss:=[4,1,2,3,1,2,4,3]ˆT01231243[i];
cst[prodim(1, ts, ss)] := ss;
end for;
m:=0; for i in [1..165] do if cst[i] ne []
then m:=m+1; end if; end for; m;
Orbits(N01231243s);
198
Appendix D: MAGMA Code for
Isomorphism Type of L
2
(11) × 3
S:=Sym(4);
xx:=S!(1,2)(3,4);
yy:=S!(1,2,3);
N:=sub<S|xx,yy>;
G<x,y,t>:=Group<x,y,t|xˆ2,yˆ3,(x
*
y)ˆ3,(yˆ-1
*
xˆ-1
*
y
*
x)ˆ2,tˆ2,
(t,y),(x
*
t)ˆ5>;
f,G1,k:=CosetAction(G,sub<G|x,y>);
CompositionFactors(G1);
Center(G1);
NL:=NormalLattice(G1); NL;
MinimalNormalSubgroups(G1);
D:=DirectProduct(CyclicGroup(3),PSL(2,11));
s:=IsIsomorphic(D,G1); s;
a:=NL[3].1;
b:=NL[3].2;
Order(a);
Order(b);
Order(a
*
b);
H<a,b>:=Group<a,b|aˆ2,bˆ3,(a
*
b)ˆ11,(a,b
*
a
*
b
*
a
*
b)ˆ2>; #H;
f1,H1,k1:=CosetAction(H,sub<H|Id(H)>);
s:=IsIsomorphic(H1,PSL(2,11));
s;
HH<a,b,c>:=Group<a,b,c|aˆ2,bˆ3,(a
*
b)ˆ11,(a,b
*
a
*
b
*
a
*
b)ˆ2,
cˆ3,(a,c),(b,c)>;
#HH;
f2,H2,k2:=CosetAction(HH,sub<HH|Id(HH)>);
s:=IsIsomorphic(H2,G1);
s;
199
Appendix E: MAGMA Code for
Factoring L
2
(11) × 3 by the center
of G
S:=Sym(4);
xx:=S!(1,2)(3,4);
yy:=S!(1,2,3);
N:=sub<S|xx,yy>;
Stabiliser(N,4);
#N;
G<x,y,t>:=Group<x,y,t|xˆ2,yˆ3,(x
*
y)ˆ3,(yˆ-1
*
xˆ-1
*
y
*
x)ˆ2,tˆ2,
(t,y),(x
*
t)ˆ5>;
f,G1,k:=CosetAction(G,sub<G|x,y>);
IN:=sub<G1|f(x),f(y)>;
CompositionFactors(G1);
#DoubleCosets(G,sub<G|x,y>,sub<G|x,y>);
Index(G,sub<G|x,y>);
Sch;
Center(G1);
No:=NormalSubgroups(G1);
No;
Center(G1).1;
f(t
*
(tˆx)ˆy
*
((tˆx)ˆy)ˆy
*
tˆ(x)
*
(tˆx)ˆy
*
((tˆx)ˆy)ˆy
*
t
*
tˆ(x))ˆ-1;
f(t
*
(tˆx)ˆy
*
((tˆx)ˆy)ˆy
*
tˆ(x)
*
(tˆx)ˆy
*
((tˆx)ˆy)ˆy
*
t
*
tˆ(x)) eq
f(x
*
y
*
x);
G<x,y,t>:=Group<x,y,t|xˆ2,yˆ3,(x
*
y)ˆ3,(yˆ-1
*
xˆ-1
*
y
*
x)ˆ2,tˆ2,
(t,y),(x
*
t)ˆ5,(t
*
(tˆx)ˆy
*
((tˆx)ˆy)ˆy
*
tˆ(x)
*
(tˆx)ˆy
*
((tˆx)ˆy)ˆy
*
t
*
tˆ(x))=(x
*
y
*
x)>;
f,G1,k:=CosetAction(G,sub<G|x,y>);
CompositionFactors(G1);
IN:=sub<G1|f(x),f(y)>;
200
#G;
#DoubleCosets(G,sub<G|x,y>,sub<G|x,y>);
Index(G,sub<G|x,y>);
201
Appendix F: MAGMA Code for
Isomorphism Type of P GL
2
(11)
S:=Sym(5);
xx:=S!(1,2,3,4,5);
yy:=S!(1,4)(2,3);
N:=sub<S|xx,yy>;
N0:=Stabiliser(N,5);
N0;
G<x,y,t>:=Group<x,y,t|xˆ5,yˆ2,(x
*
y)ˆ2,tˆ2,(t,y),(x
*
t)ˆ5,
(x
*
t
*
(tˆx))ˆ3>;
#G;
f,G1,k:=CosetAction(G,sub<G|x,y>);
CompositionFactors(G1);
Q:={}; for i in [1..10] do Q:=Q join {iˆ2 mod 11}; end for;
Q;
T:={}; for i in Q do T:=T join {iˆ2 mod 11};
if T eq Q then i; end if; end for;
//
*
the following code will give all the 11 elements
inverses by replacing i with all 11 elemnts each time
*
//
F:=GaloisField(11);
F!1ˆ-1; F!2ˆ-1; F!3ˆ-1; F!4ˆ-1; F!5ˆ-1;
F!6ˆ-1; F!7ˆ-1; F!8ˆ-1; F!9ˆ-1; F!10ˆ-1;
/
*
let k=9
*
/
S:=Sym(12);
alpha:=S!(1,2,3,4,5,6,7,8,9,10,11);
beta:=S!(1,9,4,3,5)(2,7,8,6,10);
gamma:=S!(12,11)(1,10)(2,5)(3,7)(4,8)(6,9);
//
*
N here is L(2,11) because L(2,11)=<alpha, beta, gamma>
and PGL(2,11)=<alpha, beta, gamma, delta>, delta here
is equal to (aut) which is a map that takes (x) to (-x)
*
//
N:=sub<S|alpha,beta,gamma>;
#N;
202
s,u:=IsIsomorphic(PSL(2,11),N);
s;
aut:=S!(1,10)(2,9)(3,8)(4,7)(5,6);
pgl211:=sub<S|N,aut>;
#pgl211;
s1,u1:=IsIsomorphic(PGL(2,11),pgl211);
s1;
s2,u2:=IsIsomorphic(G1,pgl211);
s2;
u2;
xx:=pgl211!(1, 5, 8, 11, 4)(6, 7, 12, 9, 10);
yy:=pgl211!(1, 5)(2, 3)(4, 8)(6, 7)(10, 12);
tinf:=pgl211!(1, 4)(2, 6)(3, 7)(5, 8)(9, 11)(10, 12);
MaximalSubgroups(pgl211);
t1:=tinfˆxx; t1;
t2:=t1ˆxx; t2;
t3:=t2ˆxx; t3;
t0:=t3ˆxx; t0;
tinf;
t0
*
t3
*
t2
*
t1
*
tinf;
xxˆ5;
203
Appendix G: MAGMA Code for
Progenitor 2
∗8
: ((Z
4
× Z
2
) • D
4
)
NumberOfTransitiveGroups(8);
N:=TransitiveGroup(8,27);
D:=SmallGroupDatabase();
IdentifyGroup(N);
G:=SmallGroup(D,64,32);
f,G1,k:=CosetAction(G,sub<G|Id(G)>);
SL:=Subgroups(G1);
T:= {X‘subgroup: X in SL};
#T;
TrivCore:={H:H in T| #Core(G1,H) eq 1};
#TrivCore;
mdeg:=Min({Index(G1,H):H in TrivCore});
Good:={H: H in TrivCore| Index(G1,H) eq mdeg};
#Good;
H:=Rep(Good);
f,G1,K:=CosetAction(G1,H);
G1;
FPGroup(G);
G<a,b,c,d,e,r>:=Group<a,b,c,d,e,r|aˆ2=d,bˆ2,cˆ2,dˆ2,eˆ2,rˆ2,
bˆa=b
*
c,cˆa=c
*
e,cˆb=c,dˆa=d,dˆb=d
*
e,dˆc=d
*
r,eˆa=e
*
r,eˆb=e,
eˆc=e,eˆd=e,rˆa=r,rˆb=r,rˆc=r,rˆd=r,rˆe=r>;
#G;
s:=IsIsomorphic(G1,N);
s;
//
*
Now, we have a permutaion representation that isomorphic to
our transitive group. We will label the previous permutation
as a, b, c, d, e, and r.
*
//
A:=G1!(1, 2)(3, 7)(4, 5, 8, 6);
B:=G1!(1, 3)(2, 5)(4, 8)(6, 7);
C:=G1!(1, 4)(2, 6)(3, 8)(5, 7);
204
D:=G1!(4, 8)(5, 6);
E:=G1!(2, 7)(5, 6);
R:=G1!(1, 3)(2, 7)(4, 8)(5, 6);
N:=sub<G1|A,B,C,D,E,R>;
//
*
Now, we must stabilise an element t.
*
//
N0:=Stabiliser(N,8);
N0;
//
*
We must write all the elements of N0 in terms of a,b,c,d,e,
and r by using Schreier system.
*
//
NN<a,b,c,d,e,r>:=Group<a,b,c,d,e,r|aˆ2=d,bˆ2,cˆ2,dˆ2,eˆ2,
rˆ2,bˆa=b
*
c,cˆa=c
*
e,cˆb=c,dˆa=d,dˆb=d
*
e,dˆc=d
*
r,eˆa=e
*
r,
eˆb=e,eˆc=e,eˆd=e,rˆa=r,rˆb=r,rˆc=r,rˆd=r,rˆe=r>;
Sch:=SchreierSystem(NN,sub<NN|Id(NN)>);
ArrayP:=[Id(N): i in [1..64]];
for i in [2..64] do
P:=[Id(N): l in [1..#Sch[i]]];
for j in [1..#Sch[i]] do
if Eltseq(Sch[i])[j] eq 1 then P[j]:=A; end if;
if Eltseq(Sch[i])[j] eq -1 then P[j]:=Aˆ-1; end if;
if Eltseq(Sch[i])[j] eq 2 then P[j]:=B; end if;
if Eltseq(Sch[i])[j] eq 3 then P[j]:=C; end if;
if Eltseq(Sch[i])[j] eq 4 then P[j]:=D; end if;
if Eltseq(Sch[i])[j] eq 5 then P[j]:=E; end if;
if Eltseq(Sch[i])[j] eq 6 then P[j]:=R; end if;
end for;
PP:=Id(N);
for k in [1..#P] do
PP:=PP
*
P[k]; end for;
ArrayP[i]:=PP;
end for;
for i in [1..64] do
if ArrayP[i] eq N!(2, 7)(5, 6) then print Sch[i];
end if; end for;
for i in [1..64] do
if ArrayP[i] eq N!(2, 5)(6, 7) then print Sch[i];
end if; end for;
for i in [1..64] do
if ArrayP[i] eq N!(1, 3)(2, 5, 7, 6) then print Sch[i];
end if; end for;
Set(N0);
//
*
we will utilize the lemma by taking the stabiliser
of two elements and determining the centraliser of
those points.
*
//
N01:=Stabiliser(G1,[8,1]);
205
N01;
C:=Centraliser(G1,N01);
C;
Set(C);
//
*
The lemma deals with elements that have a
permutation (8,1) by itself or do not have either
1 or 8. By running Set(C), we find that there is
four elements that have a permutaion (8,1) together
and by itself such as (1, 8)(2, 6)(3, 4)(5, 7),
(1, 8)(2, 5)(3, 4)(6, 7), (1, 8)(3, 4), and
(1, 8)(2, 7)(3, 4)(5, 6).
*
//
for i in [1..64] do
if ArrayP[i] eq N!(1, 8)(2, 6)(3, 4)(5, 7) then print Sch[i];
end if; end for;
for i in [1..64] do
if ArrayP[i] eq N!(1, 8)(2, 5)(3, 4)(6, 7) then print Sch[i];
end if; end for;
for i in [1..64] do
if ArrayP[i] eq N!(1, 8)(3, 4) then print Sch[i];
end if; end for;
for i in [1..64] do
if ArrayP[i] eq N!(1, 8)(2, 7)(3, 4)(5, 6) then print Sch[i];
end if; end for;
//
*
Thus, we have have to apply the lemma as the following:
(a
*
c
*
aˆ-1
*
t)ˆk=1, (c
*
r)ˆk=1, (b
*
c
*
e)ˆk=1, or (b
*
c)ˆk=1,
where k is odd.
*
//
S:=Sym(8);
aa:=G1!(1, 2)(3, 7)(4, 5, 8, 6);
bb:=G1!(1, 3)(2, 5)(4, 8)(6, 7);
cc:=G1!(1, 4)(2, 6)(3, 8)(5, 7);
dd:=G1!(4, 8)(5, 6);
ee:=G1!(2, 7)(5, 6);
rr:=G1!(1, 3)(2, 7)(4, 8)(5, 6);
N:=sub<G1|aa,bb,cc,dd,ee,rr>;
//
*
Now, we have to insert t and with which commute into
our progenitors.
Note: t commutes with each generator of the one point
stabiliser.
*
//
for k in [1..5] do
G<a,b,c,d,e,r,t>:=Group<a,b,c,d,e,r,t|aˆ2=d,bˆ2,cˆ2,dˆ2,
eˆ2,rˆ2,bˆa=b
*
c,cˆa=c
*
e,cˆb=c,dˆa=d,dˆb=d
*
e,dˆc=d
*
r,
eˆa=e
*
r,eˆb=e,eˆc=e,eˆd=e,rˆa=r,rˆb=r,rˆc=r,rˆd=r,
rˆe=r,tˆ2,(t,e),(t,b
*
e
*
r),(t,d
*
b),(b
*
c
*
e
*
t)ˆk>; #G;
end for;
206
Appendix H: MAGMA Code for
Isomorphism Type of
((Z
4
× Z
2
) • D
4
)
S:=Sym(8);
aa:=S!(1, 2)(3, 7)(4, 5, 8, 6);
bb:=S!(1, 3)(2, 5)(4, 8)(6, 7);
cc:=S!(1, 4)(2, 6)(3, 8)(5, 7);
dd:=S!(4, 8)(5, 6);
ee:=S!(2, 7)(5, 6);
rr:=S!(1, 3)(2, 7)(4, 8)(5, 6);
N:=sub<S|aa,bb,cc,dd,ee,rr>;
NL:=NormalLattice(N);
NL;
IsAbelian(NL[4]);
A:=N!(1, 4, 3, 8)(2, 6, 7, 5);
B:=N!(2, 7)(5, 6);
NL4:=sub<N|A,B>;
T:=Transversal(N,NL4);
q,ff:=quo<N|NL4>;
IsAbelian(q);
Center(q);
nl:=NormalLattice(q);
nl;
X1:=AbelianGroup(GrpPerm,[4,2]);
IsIsomorphic(X1,NL[4]);
NumberOfGenerators(NL[4]);
NL[4] eq sub<NL[4]|NL[4].1,NL[4].2>;
A:=N!(1, 4, 3, 8)(2, 6, 7, 5);
B:=N!(2, 7)(5, 6);
NL4:=sub<N|A,B>;
207
q,ff:=quo<N|NL4>;
NumberOfGenerators(q);
q eq sub<q|q.1,q.2>;
q1:=q.1; q2:=q.2;
T:=Transversal(N,NL4);
T[1];
T2:=T[2];T2;
T3:=T[3];T3;
T23:=T[2]
*
T[3];
T23;
/
*
(1, 5, 4, 2, 3, 6, 8, 7)
*
/
q.1
*
q.2;
/
*
(1, 4)(2, 3)
*
/
ff(T[2]) eq q.1;
ff(T[3]) eq q.2;
q eq sub<q|q1,q2>;
ff(T[2]) eq q1;
ff(T[3]) eq q2;
NN<a,b>:=Group<a,b|aˆ4,bˆ2,(a,b)>;
Sch:=SchreierSystem(NN,sub<NN|Id(NN)>);
ArrayP:=[Id(NL4): i in [1..8]];
for i in [2..8] do
P:=[Id(NL4): l in [1..#Sch[i]]];
for j in [1..#Sch[i]] do
if Eltseq(Sch[i])[j] eq 1 then P[j]:=A; end if;
if Eltseq(Sch[i])[j] eq -1 then P[j]:=Aˆ-1; end if;
if Eltseq(Sch[i])[j] eq 2 then P[j]:=B; end if;
PP:=Id(NL4);
for k in [1..#P] do
PP:=PP
*
P[k]; end for;
ArrayP[i]:=PP;
end for;
end for;
I:=[Id(NN): i in [1..5]];
for i in [1..8] do if ArrayP[i] eq T23ˆ2 then Sch[i];
I[1]:=Sch[i]; end if; end for;
for i in [1..8] do if ArrayP[i] eq AˆT2 then Sch[i];
I[2]:=Sch[i]; end if; end for;
for i in [1..8] do if ArrayP[i] eq BˆT2 then Sch[i];
I[3]:=Sch[i]; end if; end for;
for i in [1..8] do if ArrayP[i] eq AˆT3 then Sch[i];
I[4]:=Sch[i]; end if; end for;
for i in [1..8] do if ArrayP[i] eq BˆT3 then Sch[i];
I[5]:=Sch[i]; end if; end for;
208
I;
H<x,y,z,w>:=Group<x,y,z,w|xˆ4,yˆ2,(x,y),zˆ4,wˆ2,
(z
*
w)ˆ2=x,xˆz=x
*
y, yˆz=xˆ2
*
y,xˆw=x
*
y,yˆw=y>;
#H;
f,h,k:=CosetAction(H,sub<H|Id(H)>);
#h;
s:=IsIsomorphic(N,h);
s;
//
*
A presentation for the progenitor is
*
//
G<a,b,c,d,e,r,t>:=Group<a,b,c,d,e,r,t|aˆ2=d,bˆ2,cˆ2,
dˆ2,eˆ2,rˆ2,bˆa=b
*
c,cˆa=c
*
e,cˆb=c,dˆa=d,dˆb=d
*
e,
dˆc=d
*
r,eˆa=e
*
r,eˆb=e,eˆc=e,eˆd=e,rˆa=r,rˆb=r,rˆc=r,
rˆd=r,rˆe=r,tˆ2,(t,e),(t,b
*
e
*
r),(t,d
*
b)>;
209
Appendix I: MAGMA Code for
Isomorphism Type of 2
•
P GL
2
(11)
//
*
We now prove that G1 is central extension of Z_2
by PGL(2,11).
*
//
S:=Sym(8);
aa:=S!(1, 2)(3, 7)(4, 5, 8, 6);
bb:=S!(1, 3)(2, 5)(4, 8)(6, 7);
cc:=S!(1, 4)(2, 6)(3, 8)(5, 7);
dd:=S!(4, 8)(5, 6);
ee:=S!(2, 7)(5, 6);
rr:=S!(1, 3)(2, 7)(4, 8)(5, 6);
N:=sub<S|aa,bb,cc,dd,ee,rr>;
G<a,b,c,d,e,r,t>:=Group<a,b,c,d,e,r,t|aˆ2=d,bˆ2,cˆ2,dˆ2,eˆ2,
rˆ2,bˆa=b
*
c,cˆa=c
*
e,cˆb=c,dˆa=d,dˆb=d
*
e,dˆc=d
*
r,eˆa=e
*
r,
eˆb=e,eˆc=e,eˆd=e,rˆa=r,rˆb=r,rˆc=r,rˆd=r,rˆe=r,tˆ2,
(t,e),(t,b
*
e
*
r),(t,d
*
b),(b
*
c
*
e
*
t)ˆ3,(e
*
b
*
tˆa
*
t)ˆ5>;
f,G1,k:=CosetAction(G,sub<G|Id(G)>);
SL:=Subgroups(G1);
T:={X‘subgroup:X in SL};
TrivCore:={H:H in T| #Core(G1,H) eq 1};
mdeg:=Min({Index(G1,H):H in TrivCore});
Good:={H:H in TrivCore|Index(G1,H) eq mdeg};
H:=Rep(Good);
f,G1,k:=CosetAction(G1,H);
#G; #k;
NL:=NormalLattice(G1);
q,ff:=quo<G1|NL[2]>;
H<x,y,z,w>:=Group<x,y,z,w|xˆ2,yˆ2,zˆ2,wˆ2,(x
*
y)ˆ4,(x
*
z)ˆ2,
(x
*
w)ˆ10,(y
*
z)ˆ2,(y
*
w)ˆ2,(z
*
w)ˆ6,(x,y)ˆ2,(x,w)ˆ5,(z,w)ˆ3,
(x
*
y
*
z)ˆ4,(x
*
y
*
w)ˆ12,(x
*
z
*
w)ˆ10,(xˆy
*
z)ˆ2,(xˆz
*
w)ˆ10,
(x
*
y,z),(x
*
z,w)ˆ5,(x
*
y
*
z,w)ˆ5,(x
*
y
*
w,z)ˆ3,(x
*
y,z
*
w)ˆ5,
(x
*
z,y
*
w)ˆ6,(x
*
w,y
*
z)ˆ2,(w
*
x,y
*
z)ˆ2, ((x
*
w)ˆ2
*
y
*
z)ˆ5,
210
(x
*
y
*
z
*
w)ˆ12,(x
*
y
*
(z
*
w)ˆ2)ˆ10,(x
*
z
*
y
*
w
*
x
*
y)ˆ2,
(x
*
w
*
z
*
y
*
w
*
x)ˆ2,(w
*
x
*
y
*
w
*
z
*
x
*
y
*
w)ˆ2,(x,y
*
z
*
w
*
y
*
z
*
w
*
z
*
w)ˆ2,
(x
*
y
*
z
*
y
*
w)ˆ10,(y
*
x
*
w
*
z
*
x
*
y
*
w
*
z)ˆ5,(y,xˆz
*
y
*
z
*
w
*
z
*
x
*
y
*
w)ˆ3,
(x
*
y
*
z
*
y
*
x
*
w
*
y
*
w
*
z
*
y
*
w
*
x)ˆ10,(x
*
y
*
z
*
w,y
*
z
*
x
*
w
*
y
*
z
*
w
*
y)ˆ2,
(x
*
y
*
z, w
*
y
*
x)ˆ5,(x
*
z
*
y
*
w,w
*
x
*
z
*
y)ˆ3,
(x
*
z
*
y
*
w
*
x
*
y
*
w
*
z
*
x
*
y
*
w
*
z
*
y
*
x
*
w)ˆ5,(x
*
w
*
y
*
z
*
w
*
z
*
y
*
x
*
w)ˆ5>;
f,h,k:=CosetAction(H,sub<H|Id(H)>);
#h;
s:=IsIsomorphic(q,h);
T:=Transversal(G1,NL[2]);
ff(T[2]) eq q.1;
ff(T[3]) eq q.2;
ff(T[4]) eq q.3;
ff(T[5]) eq q.7;
Order(T[2]), Order(T[3]), Order(T[4]), Order(T[5]);
Order(q.1);
T[2]ˆ2;
NL[2];
K<x,y,z,w,c>:=Group<x,y,z,w,c|xˆ2=c,yˆ2,zˆ2,wˆ2,(x
*
y)ˆ4,
(x
*
z)ˆ2=c,(x
*
w)ˆ10=c,(y
*
z)ˆ2,(y
*
w)ˆ2,(z
*
w)ˆ6,(x,y)ˆ2,(x,w)ˆ5,
(z,w)ˆ3,(x
*
y
*
z)ˆ4,(x
*
y
*
w)ˆ12,(x
*
z
*
w)ˆ10=c,(xˆy
*
z)ˆ2=c,
(xˆz
*
w)ˆ10=c,(x
*
y,z),(x
*
z,w)ˆ5,(x
*
y
*
z,w)ˆ5,(x
*
y
*
w,z)ˆ3,
(x
*
y,z
*
w)ˆ5,(x
*
z,y
*
w)ˆ6,(x
*
w,y
*
z)ˆ2,(w
*
x,y
*
z)ˆ2,
((x
*
w)ˆ2
*
y
*
z)ˆ5=c,(x
*
y
*
z
*
w)ˆ12,(x
*
y
*
(z
*
w)ˆ2)ˆ10=c,
(x
*
z
*
y
*
w
*
x
*
y)ˆ2,(x
*
w
*
z
*
y
*
w
*
x)ˆ2,(w
*
x
*
y
*
w
*
z
*
x
*
y
*
w)ˆ2,
(x,y
*
z
*
w
*
y
*
z
*
w
*
z
*
w)ˆ2,(x
*
y
*
z
*
y
*
w)ˆ10=c,
(y
*
x
*
w
*
z
*
x
*
y
*
w
*
z)ˆ5=c,(y,xˆz
*
y
*
z
*
w
*
z
*
x
*
y
*
w)ˆ3,
(x
*
y
*
z
*
y
*
x
*
w
*
y
*
w
*
z
*
y
*
w
*
x)ˆ10=c,(x
*
y
*
z
*
w,y
*
z
*
x
*
w
*
y
*
z
*
w
*
y)ˆ2,
(x
*
y
*
z, w
*
y
*
x)ˆ5,(x
*
z
*
y
*
w,w
*
x
*
z
*
y)ˆ3,
(x
*
z
*
y
*
w
*
x
*
y
*
w
*
z
*
x
*
y
*
w
*
z
*
y
*
x
*
w)ˆ5,(x
*
w
*
y
*
z
*
w
*
z
*
y
*
x
*
w)ˆ5=c>;
f,kk,k:=CosetAction(K,sub<K|Id(K)>);
#kk;
s:=IsIsomorphic(G1,kk);
211
Appendix J: MAGMA Code for
Isomorphism Type of (A
5
× A
5
) : 4
S:=Sym(8);
aa:=S!(1, 2)(3, 7)(4, 5, 8, 6);
bb:=S!(1, 3)(2, 5)(4, 8)(6, 7);
cc:=S!(1, 4)(2, 6)(3, 8)(5, 7);
dd:=S!(4, 8)(5, 6);
ee:=S!(2, 7)(5, 6);
rr:=S!(1, 3)(2, 7)(4, 8)(5, 6);
N:=sub<S|aa,bb,cc,dd,ee,rr>;
G<a,b,c,d,e,r,t>:=Group<a,b,c,d,e,r,t|aˆ2=d,bˆ2,cˆ2,dˆ2,eˆ2,
rˆ2,bˆa=b
*
c,cˆa=c
*
e,cˆb=c,dˆa=d,dˆb=d
*
e,dˆc=d
*
r,eˆa=e
*
r,
eˆb=e,eˆc=e,eˆd=e,rˆa=r,rˆb=r,rˆc=r,rˆd=r,rˆe=r,tˆ2,(t,e),
(t,b
*
e
*
r),(t,d
*
b),(b
*
c
*
e
*
t)ˆ5,(e
*
r
*
t)ˆ3,(a
*
(tˆr)ˆc)ˆ4>;
f,G1,k:=CosetAction(G,sub<G|a,b,c,d,e,r>);
#G; #k;
CompositionFactors(G1);
Center(G1);
NL:=NormalLattice(G1);
NL;
MinimalNormalSubgroups(G1);
D:=DirectProduct(Alt(5),Alt(5));
s:=IsIsomorphic(D,NL[2]);
s;
H<a,b,c,d>:=Group<a,b,c,d|aˆ3,bˆ2,(a
*
b)ˆ5,cˆ3,dˆ2,(c
*
d)ˆ5,
(a,c),(a,d),(b,c),(b,d)>;
f,H1,k:=CosetAction(H,sub<H|Id(H)>);
#H;
s,t:=IsIsomorphic(H1,NL[2]);
s;
a:=t(f(a));
b:=t(f(b));
212
c:=t(f(c));
d:=t(f(d));
for g in G1 do if Order(g) eq 4 and g notin NL[2] and G1 eq
sub<G1|NL[2],g
then U:=g; break; end if; end for;
U;
G1 eq sub<G1|NL[2],U>;
N:=sub<G1|a,b,c,d>;
#N;
N eq NL[2];
NN<i,j,l,m>:=Group<i,j,l,m|iˆ3,jˆ2,(i
*
j)ˆ5,lˆ3,mˆ2,(l
*
m)ˆ5,
(i,l),(i,m),(j,l),(j,m)>;
#NN;
Sch:=SchreierSystem(NN,sub<NN|Id(NN)>);
ArrayP:=[Id(N): i in [1..3600]];
for i in [2..3600] do
P:=[Id(N): l in [1..#Sch[i]]];
for j in [1..#Sch[i]] do
if Eltseq(Sch[i])[j] eq 1 then P[j]:=a; end if;
if Eltseq(Sch[i])[j] eq -1 then P[j]:=aˆ-1; end if;
if Eltseq(Sch[i])[j] eq 2 then P[j]:=b; end if;
if Eltseq(Sch[i])[j] eq 3 then P[j]:=c; end if;
if Eltseq(Sch[i])[j] eq -3 then P[j]:=cˆ-1; end if;
if Eltseq(Sch[i])[j] eq 4 then P[j]:=d; end if;
end for;
PP:=Id(N);
for k in [1..#P] do
PP:=PP
*
P[k]; end for;
ArrayP[i]:=PP;
end for;
A:=[Id(NN): i in [1..3]];
for i in [1..3600] do
if aˆU eq ArrayP[i] then A[1]:=Sch[i]; Sch[i];
end if; end for;
for i in [1..3600] do
if bˆU eq ArrayP[i] then A[2]:=Sch[i]; Sch[i];
end if; end for;
for i in [1..3600] do
if cˆU eq ArrayP[i] then A[3]:=Sch[i]; Sch[i];
end if; end for;
for i in [1..3600] do
if dˆU eq ArrayP[i] then A[4]:=Sch[i]; Sch[i];
end if; end for;
HH<a,b,c,d,e>:=Group<a,b,c,d,e|aˆ3,bˆ2,(a
*
b)ˆ5,cˆ3,dˆ2,
213
(c
*
d)ˆ5,(a,c),(a,d),(b,c),(b,d),eˆ4,aˆe=d
*
cˆ-1
*
d
*
c
*
d
*
c,
bˆe=d
*
c
*
d
*
cˆ-1
*
d,cˆe=b
*
aˆ-1
*
b
*
a
*
b
*
a,
dˆe=a
*
b
*
a
*
b
*
aˆ-1
*
b
*
aˆ-1>;
f2,H2,k2:=CosetAction(HH,sub<HH|Id(HH)>);
#HH;
s:=IsIsomorphic(H2,G1);
s;
214
Appendix K: MAGMA Code for
The Progenitor 2
∗6
: (Z
3
o Z
2
)
G<a,b,c>:=Group<a,b,c|aˆ3,bˆ3,cˆ2,(a,b),aˆc=b, bˆc=a>;
#G;
W:=WreathProduct(CyclicGroup(3),CyclicGroup(2));
#W;
CC:=Classes(W);
CC;
for i in [1..#CC] do if CC[i][1] eq 2 then i; end if; end for;
for i in [1..#CC] do if CC[i][1] eq 3 then i; end if; end for;
for C in Class(W,CC[2][3]) do for A,B in Class(W,CC[5][3])
join Class(W,CC[6][3]) do if Order(A) eq 3 and Order(B) eq 3
and Order(C) eq 2 and (A,B) eq Id(W) and AˆC eq B and BˆC eq A
and W eq sub<W|A,B,C> then A,B,C; break; end if; end for;
end for;
Generators(G);
S:=Sym(6);
A:=S!(4, 5, 6);
B:=S!(1, 2, 3);
C:=S!(1, 5)(2, 6)(3, 4);
N:=sub<S|A,B,C>;
N eq W;
N1:=Stabiliser(N,1);
N1;
#N;
NN:=G;
Sch:=SchreierSystem(NN,sub<NN|Id(NN)>);
ArrayP:=[Id(N): i in [1..18]];
for i in [2..18] do
P:=[Id(N): l in [1..#Sch[i]]];
for j in [1..#Sch[i]] do
if Eltseq(Sch[i])[j] eq 1 then P[j]:=A; end if;
215
if Eltseq(Sch[i])[j] eq -1 then P[j]:=Aˆ-1; end if;
if Eltseq(Sch[i])[j] eq 2 then P[j]:=B; end if;
if Eltseq(Sch[i])[j] eq -2 then P[j]:=Bˆ-1; end if;
if Eltseq(Sch[i])[j] eq 3 then P[j]:=C; end if;
end for;
PP:=Id(N);
for k in [1..#P] do
PP:=PP
*
P[k]; end for;
ArrayP[i]:=PP;
end for;
for i in [1..18] do if ArrayP[i] eq N!(4, 5, 6)
then print Sch[i]; end if; end for;
H<A,B,C,t>:=Group<A,B,C,t|Aˆ3, Bˆ3, Cˆ2, (A,B),
AˆC=B, BˆC=A, tˆ2, (t,A)>;
#H;
//
*
with lemma
*
//
N0:=Stabiliser(N,6);
N0;
N01:=Stabiliser(N,[6,1]);
N01;
Centraliser(N,N01);
Set(Centraliser(N,N01));
#N;
for i in [1..18] do if ArrayP[i] eq N!(1,6)(2,4)(3,5)
then print Sch[i]; end if; end for;
for k in [0..5] do
H<A,B,C,t>:=Group<A,B,C,t|Aˆ3,Bˆ3,Cˆ2,(A,B),AˆC=B,
BˆC=A,tˆ2,(t,B),(B
*
C
*
Bˆ-1
*
t)ˆk>; #H; end for;
#H;
216
Appendix L: MAGMA Code for
Monomial Progenitor
3
∗12
:
m
(2
•
A
5
)
S:=Sym(24);
a:=S!(1,2,5,4)(3,6,8,7)(9,13,11,14)(10,15,12,16)
(17,19,18,20)(21,24,23,22);
b:=S!(1,3,2)(4,5,8)(6,9,10)(7,11,12)(13,16,17)
(14,15,18)(19,21,22)(20,23,24);
G1:=sub<S|a,b>;
S:=Subgroups(G1);
#S;
for i in [1..#S] do i, Index(G1,S[i]‘subgroup);
end for;
CT:=CharacterTable(G1);CT;
N:=S[7]‘subgroup;
#N;
N;
N eq sub<G1|N.1,N.2>;
N:=sub<G1|(1, 23, 3, 15, 17)(2, 19, 12, 6, 22)
(4, 20, 10, 7, 24)(5, 21, 8, 16, 18),(1, 5)(2, 4)
(3, 8)(6, 7)(9, 11)(10, 12)(13, 14)(15, 16)(17, 18)
(19, 20)(21, 23)(22, 24)>;
#N;
CN:=Classes(N);
CN;
CharacterTable(N);
chN:=LinearCharacters(N);
chN;
#chN;
#chN[2];
217
chN[2](N.1);
chN[2](N.2);
ind:=Induction(chN[2],G1);
ind;
IsFaithful(ind);
Norm(ind);
for i in [1..9] do if ind eq CT[i] then i; end if; end for;
T:=RightTransversal(G1,N);
T; #T;
A:=[0:i in [1..144]];
for i in [1..12] do if a
*
T[i]ˆ-1 in N then i,
chN[2](a
*
T[i]ˆ-1); end if; end for;
for i in [1..12] do if T[2]
*
a
*
T[i]ˆ-1 in N then i,
chN[2](T[2]
*
a
*
T[i]ˆ-1); end if; end for;
for i in [1..12] do if T[3]
*
a
*
T[i]ˆ-1 in N then i,
chN[2](T[3]
*
a
*
T[i]ˆ-1); end if; end for;
for i in [1..12] do if T[4]
*
a
*
T[i]ˆ-1 in N then i,
chN[2](T[4]
*
a
*
T[i]ˆ-1); end if; end for;
for i in [1..12] do if T[5]
*
a
*
T[i]ˆ-1 in N then i,
chN[2](T[5]
*
a
*
T[i]ˆ-1); end if; end for;
for i in [1..12] do if T[6]
*
a
*
T[i]ˆ-1 in N then i,
chN[2](T[6]
*
a
*
T[i]ˆ-1); end if; end for;
for i in [1..12] do if T[7]
*
a
*
T[i]ˆ-1 in N then i,
chN[2](T[7]
*
a
*
T[i]ˆ-1); end if; end for;
for i in [1..12] do if T[8]
*
a
*
T[i]ˆ-1 in N then i,
chN[2](T[8]
*
a
*
T[i]ˆ-1); end if; end for;
for i in [1..12] do if T[9]
*
a
*
T[i]ˆ-1 in N then i,
chN[2](T[9]
*
a
*
T[i]ˆ-1); end if; end for;
for i in [1..12] do if T[10]
*
a
*
T[i]ˆ-1 in N then i,
chN[2](T[10]
*
a
*
T[i]ˆ-1); end if; end for;
for i in [1..12] do if T[11]
*
a
*
T[i]ˆ-1 in N then i,
chN[2](T[11]
*
a
*
T[i]ˆ-1); end if; end for;
for i in [1..12] do if T[12]
*
a
*
T[i]ˆ-1 in N then i,
chN[2](T[12]
*
a
*
T[i]ˆ-1); end if; end for;
A:=[0:i in [1..144]];
A[2]:=1;
A[13]:=-1;
A[28]:=-1;
A[39]:=1;
A[57]:=1;
A[71]:=-1;
A[84]:=1;
218
A[94]:=1;
A[101]:=-1;
A[116]:=-1;
A[126]:=1;
A[139]:=-1;
A;
B:=[0:i in [1..144]];
for i in [1..12] do if b
*
T[i]ˆ-1 in N then i,
chN[2](b
*
T[i]ˆ-1); end if; end for;
for i in [1..12] do if T[2]
*
b
*
T[i]ˆ-1 in N then i,
chN[2](T[2]
*
b
*
T[i]ˆ-1); end if; end for;
for i in [1..12] do if T[3]
*
b
*
T[i]ˆ-1 in N then i,
chN[2](T[3]
*
b
*
T[i]ˆ-1); end if; end for;
for i in [1..12] do if T[4]
*
b
*
T[i]ˆ-1 in N then i,
chN[2](T[4]
*
b
*
T[i]ˆ-1); end if; end for;
for i in [1..12] do if T[5]
*
b
*
T[i]ˆ-1 in N then i,
chN[2](T[5]
*
b
*
T[i]ˆ-1); end if; end for;
for i in [1..12] do if T[6]
*
b
*
T[i]ˆ-1 in N then i,
chN[2](T[6]
*
b
*
T[i]ˆ-1); end if; end for;
for i in [1..12] do if T[7]
*
b
*
T[i]ˆ-1 in N then i,
chN[2](T[7]
*
b
*
T[i]ˆ-1); end if; end for;
for i in [1..12] do if T[8]
*
b
*
T[i]ˆ-1 in N then i,
chN[2](T[8]
*
b
*
T[i]ˆ-1); end if; end for;
for i in [1..12] do if T[9]
*
b
*
T[i]ˆ-1 in N then i,
chN[2](T[9]
*
b
*
T[i]ˆ-1); end if; end for;
for i in [1..12] do if T[10]
*
b
*
T[i]ˆ-1 in N then i,
chN[2](T[10]
*
b
*
T[i]ˆ-1); end if; end for;
for i in [1..12] do if T[11]
*
b
*
T[i]ˆ-1 in N then i,
chN[2](T[11]
*
b
*
T[i]ˆ-1); end if; end for;
for i in [1..12] do if T[12]
*
b
*
T[i]ˆ-1 in N then i,
chN[2](T[12]
*
b
*
T[i]ˆ-1); end if; end for;
B[3]:=1;
B[16]:=1;
B[29]:=1;
B[43]:=1;
B[49]:=1;
B[72]:=-1;
B[74]:=1;
B[93]:=1;
B[106]:=1;
B[116]:=1;
B[126]:=-1;
B[143]:=1;
B;
219
M:=GL(12,3);
A:=M!A;A;
B:=M!B;B;
Order(A), Order(B), Order(A
*
B);
H:=sub<M|A,B>;
#H;
s:=IsIsomorphic(H,G1);
s;
CompositionFactors(H);
S:=Sym(24);
xx:=S!(1,3,2,4)(5,8,6,7)(9,17,10,18)(11,22,12,21)
(13,23,14,24)(15,19,16,20);
yy:=S!(1,5,9)(2,6,10)(3,7,13)(4,8,14)(11,24,22)
(12,23,21)(15,17,19)(16,18,20);
Order(xx);
Order(yy);
Order(xx
*
yy);
Order((xxˆ2,yy));
N:=sub<S|xx,yy>;
#N;
GG:=sub<N|Id(N)>;
SS:=Stabiliser(N,{1,2});
SS;
for g in N do if {1,2}ˆg eq {1,2} then GG:=sub<N|GG,g>;
end if; end for;
GG eq SS;
SS eq sub<N|(5, 11, 24, 10, 19)(6, 12, 23, 9, 20)
(7, 15, 17, 14, 21)(8, 16, 18, 13, 22),(1, 2)(3, 4)
(5, 6)(7, 8)(9, 10)(11, 12)(13, 14)(15, 16)(17, 18)
(19, 20)(21, 22)(23, 24)>;
NN<i,j>:=Group<i,j|iˆ4,jˆ3,(i
*
j)ˆ5,(iˆ2,j)>;
#NN;
Sch:=SchreierSystem(NN,sub<NN|Id(NN)>);
ArrayP:=[Id(N): i in [1..120]];
for i in [2..120] do
P:=[Id(N): l in [1..#Sch[i]]];
for j in [1..#Sch[i]] do
if Eltseq(Sch[i])[j] eq 1 then P[j]:=xx; end if;
if Eltseq(Sch[i])[j] eq -1 then P[j]:=xxˆ-1; end if;
if Eltseq(Sch[i])[j] eq 2 then P[j]:=yy; end if;
if Eltseq(Sch[i])[j] eq -2 then P[j]:=yyˆ-1; end if;
end for;
PP:=Id(N);
for k in [1..#P] do
220
PP:=PP
*
P[k]; end for;
ArrayP[i]:=PP;
end for;
for i in [1..120] do if ArrayP[i] eq N!(5, 11, 24, 10, 19)
(6, 12, 23, 9, 20)(7, 15, 17, 14, 21)(8, 16, 18, 13, 22)
then Sch[i]; end if; end for;
for i in [1..120] do if ArrayP[i] eq N!(1, 2)(3, 4)(5, 6)
(7, 8)(9, 10)(11, 12)(13, 14)(15, 16)(17, 18)(19, 20)(21,22)
(23, 24) then Sch[i]; end if; end for;
SS eq sub<N|xx
*
yy
*
xx
*
yyˆ-1,xxˆ2>;
G<x,y,t>:=Group<x,y,t|xˆ4,yˆ3,(x
*
y)ˆ5,(xˆ2,y),tˆ3,
(t,x
*
y
*
x
*
yˆ-1),tˆ(xˆ2)
*
tˆ-2>;
#G;
P<x,y,t>:=Group<x,y,t|xˆ4,yˆ3,(x
*
y)ˆ5,(xˆ2,y),tˆ3,
(t,x
*
y
*
x
*
yˆ-1),tˆ(xˆ2)
*
tˆ-2>;
D:=AlmostSimpleGroupDatabase();
for i in [1..#D] do G1:=GroupData(D,i)‘permrep;
sg:=GroupData(D,i)‘subgens; if #sg eq 0 then
G:=sub<G1|G1.1,G1.2>; else
F:=Parent(sg[1]); t:=Ngens(G1)-2; phi:= hom<F -> G1
|[G1.(i+2) : i in [1..t]] cat [Id(G1) : i in
[t+1..Ngens(F)]]>;
G:=sub <G1 | G1.1, G1.2, [phi(s): s in sg]>; end if;
if #Homomorphisms(P,G: Limit:=1) gt 0 then
GroupData(D,i)‘name; end if; end for;
221
Appendix M: MAGMA Code for
Monomial Progenitor 3
∗7
:
m
L
2
(7)
perm:=function(n,p,mat)
C<u>:=CyclotomicField(p);
Z:=Integers ();
s:=[];
for i in [1..n] do
s[i]:=i;
end for;
z:=Matrix(C,1,n,s)
*
mat;
w:=[];
for i in [1..n] do
j:=0; done:=0;
repeat
if z[1,i]/uˆj in Z then
if Z!(z[1,i]/uˆj) ge 0 then
w[i]:=n
*
j+Z!(z[1,i]/uˆj);
done:=1;
end if; end if;
j:=j+1;
until done eq 1 or j eq p;
end for;
for i in [1..(p-1)] do
for a in [1..n] do
w[a+i
*
n]:=(Z!w[a]+i
*
n-1) mod (p
*
n) + 1;
end for; end for;
S:=Sym(n
*
p);
w:=S!w;
return wˆ-1;
end function;
G<x,y>:=Group<x,y|xˆ2,yˆ3,(x
*
y)ˆ7,(x,y)ˆ4>;
S:=Sym(7);
222
xx:=S!(2,4)(3,5);
yy:=S!(1,2,3)(5,6,7);
G1:=sub<S|xx,yy>;
#G1;
#G;
S:=Subgroups(G1);
for i in [1..#S] do if Index(S[i]‘subgroup,DerivedGroup
(S[i]‘subgroup)) eq 2 then Index(G1,S[i]‘subgroup), i;
end if; end for;
H:=S[13]‘subgroup;
H;
H:=sub<G1|(2, 7)(3, 6),(1, 2, 4)(3, 6, 5),(1, 2)(4, 7),
(1, 4)(2, 7)>;
#H;
n:=Index(G1,H);n;
dH:=DerivedGroup(H);
#H/#dH;
f,g:=CosetAction(H,dH);
#Generators(H);
f(H.1), f(H.2),f(H.3), f(H.4);
C<u>:=CyclotomicField(2);
M:=MatrixAlgebra(C,1);
HM:=GModule(H,[M![u],M![1],M![1],M![1]]);
I:=Induction(HM,G1);
Norm(Character(I));
GP:=MatrixGroup(I);
#GP;
GP;
mat1:=GP.1; mat2:=GP.2;
A:=perm(7,2,mat1);
B:=perm(7,2,mat2);
A; B;
G2:=sub<Sym(14)|A,B>;
s,t:=IsIsomorphic(G1,G2);
s;
t;
A,B;
G2;
a:=G2.1;
Order(a);
b:=G2.2;
Order(b);
G2:=sub<G2|a,b>;
Order(a
*
b);
223
Order((a,b));
H<a,b>:=Group<a,b|aˆ2,bˆ3,(a
*
b)ˆ7,(a,b)ˆ4>;
#H;
f2,h2,k2:=CosetAction(H,sub<H|Id(H)>);
CompositionFactors(h2);
N:=G2;
NN<a,b>:=Group<a,b|aˆ2,bˆ3,(a
*
b)ˆ7,(a,b)ˆ4>;
#NN;
Sch:=SchreierSystem(NN,sub<NN|Id(NN)>);
ArrayP:=[Id(G2): i in [1..168]];
for i in [2..168] do
P:=[Id(N): l in [1..#Sch[i]]];
for j in [1..#Sch[i]] do
if Eltseq(Sch[i])[j] eq 1 then P[j]:=A; end if;
if Eltseq(Sch[i])[j] eq 2 then P[j]:=B; end if;
if Eltseq(Sch[i])[j] eq -2 then P[j]:=Bˆ-1; end if;
end for;
PP:=Id(G2);
for k in [1..#P] do
PP:=PP
*
P[k]; end for;
ArrayP[i]:=PP;
end for;
G22:=Stabiliser(G2,{7,14});
G22;
c:=G22.1; c;
d:=G22.2; d;
e:=G22.3; e;
c:=G2!(1, 4, 10)(2, 5, 6)(3, 8, 11)(9, 12, 13);
d:=G2!(1, 8)(2, 9)(3, 13)(4, 12)(5, 11)(6, 10);
e:=G2!(1, 8)(3, 4)(5, 6)(7, 14)(10, 11)(12, 13);
G22 eq sub<G2|c,d,e>;
for i in [1..#G2] do if ArrayP[i] eq c then Sch[i];
end if; end for;
for i in [1..#G2] do if ArrayP[i] eq d then Sch[i];
end if; end for;
for i in [1..#G2] do if ArrayP[i] eq e then Sch[i];
end if; end for;
G22 eq sub<G2|B
*
A
*
Bˆ-1
*
A
*
B
*
A
*
B
*
A
*
Bˆ-1
*
A
*
B,
B
*
A
*
Bˆ-1
*
A
*
B
*
A
*
Bˆ-1, A>;
for k,l,m,n,o,p in [0..16] do
G<x,y,t>:=Group<x,y,t|xˆ2,yˆ3,(x
*
y)ˆ7,(x,y)ˆ4, tˆ3,
tˆ(y
*
x
*
yˆ-1
*
x
*
y
*
x
*
y
*
x
*
yˆ-1
*
x
*
y)
*
tˆ-1,
tˆ(y
*
x
*
yˆ-1
*
x
*
y
*
x
*
yˆ-1)
*
tˆ-1,tˆx=tˆ-1,(x
*
y
*
t)ˆk,
(x
*
tˆy
*
tˆ2)ˆl,(xˆy
*
t)ˆm,(yˆx
*
tˆ2
*
t)ˆn,(yˆ2
*
(x
*
y)ˆ5
*
t)ˆo,
224
(x
*
yˆ-1
*
t)ˆp>; if Index(G,sub<G|x,y>) gt 7 then
k,l,m,n,o,p,Index(G,sub<G|x,y>),#G; end if; end for;
225
Appendix N: MAGMA Code for
DCE of A
7
over L
2
(7)
/
*
This is A7 homographic image of the
progenitor 3star7:L2(7)(2 double cosets,15 single cosets)
*
/
-----------------------------------------------------
S:=Sym(14);
xx:=S!(1, 8)(3, 4)(5, 6)(7, 14)(10, 11)(12, 13);
yy:=S!(1, 2, 3)(4, 5, 7)(8, 9, 10)(11, 12, 14);
N:=sub<S|xx,yy>;
#N;
k:=0; l:=0; m:=0; n:=0; o:=4;
G<x,y,t>:=Group<x,y,t|xˆ2,yˆ3,(x
*
y)ˆ7,(x,y)ˆ4, tˆ3,
tˆ(y
*
x
*
yˆ-1
*
x
*
y
*
x
*
y
*
x
*
yˆ-1
*
x
*
y)
*
tˆ-1,
tˆ(y
*
x
*
yˆ-1
*
x
*
y
*
x
*
yˆ-1)
*
tˆ-1,tˆx=tˆ-1,(x
*
y
*
t)ˆk,
(x
*
tˆy
*
tˆ2)ˆl,(xˆy
*
t)ˆm,(yˆ2
*
(x
*
y)ˆ5
*
t)ˆn,(x
*
yˆ-1
*
t)ˆo>;
f,G1,k:=CosetAction(G,sub<G|x,y>);
#G1; #k;
CompositionFactors(G1);
#sub<G|x,y>;
#DoubleCosets(G,sub<G|x,y>,sub<G|x,y>);
IN:=sub<G1|f(x),f(y)>;
DoubleCosets(G,sub<G|x,y>,sub<G|x,y>);
NN<a,b>:=Group<a,b|aˆ2,bˆ3,(a
*
b)ˆ7,(a,b)ˆ4>;
#NN;
Sch:=SchreierSystem(NN,sub<NN|Id(NN)>);
ArrayP:=[Id(N): i in [1..168]];
for i in [2..168] do
P:=[Id(N): l in [1..#Sch[i]]];
for j in [1..#Sch[i]] do
if Eltseq(Sch[i])[j] eq 1 then P[j]:=xx; end if;
if Eltseq(Sch[i])[j] eq 2 then P[j]:=yy; end if;
if Eltseq(Sch[i])[j] eq -2 then P[j]:=yyˆ-1; end if;
226
end for;
PP:=Id(N);
for k in [1..#P] do
PP:=PP
*
P[k]; end for;
ArrayP[i]:=PP;
end for;
ts:=[Id(G1): i in [1..14]];
ts[7]:=f(t); ts[1]:=f(((tˆy)ˆx)ˆy);
ts[2]:=f((((tˆy)ˆx)ˆy)ˆy); ts[3]:=f((tˆy)ˆx);
ts[4]:=f(tˆy); ts[5]:=f((tˆy)ˆy);
ts[6]:=f(((tˆy)ˆy)ˆx); ts[14]:=f(tˆx);
ts[8]:=f((((tˆx)ˆy)ˆx)ˆy); ts[9]:=f(((((tˆx)ˆy)ˆx)ˆy)ˆy);
ts[10]:=f(((tˆx)ˆy)ˆx); ts[11]:=f((tˆx)ˆy);
ts[12]:=f(((tˆx)ˆy)ˆy); ts[13]:=f((((tˆx)ˆy)ˆy)ˆx);
f((x
*
yˆ-1)ˆ4)
*
ts[11]
*
ts[13]
*
ts[12]
*
ts[7];
(xx
*
yyˆ-1)ˆ4;
f((x
*
yˆ-1)ˆ4)
*
ts[11]
*
ts[13]
*
ts[12]
*
ts[7] eq
f(((x
*
yˆ-1)
*
t)ˆ4);
for g,h in IN do if ts[7] eq g
*
(ts[14])ˆh then g,h;
end if; end for;
for i in [1..15] do i, cst[i]; end for;
for i in [1..168] do if ArrayP[i] eq
N!(7, 14)(4, 3)(5, 6)(11, 10)(12, 13)(8, 1) then Sch[i];
end if; end for;
prodim := function(pt, Q, I)
/
*
Return the image of pt under permutations Q[I]
applied sequentially.
*
/
v:=pt;
for i in I do
v:=vˆ(Q[i]);
end for;
return v;
end function;
cst:=[null: i in [1..Index(G,sub<G|x,y>)]]
where null is[Integers()|];
for i := 1 to 14 do
cst[prodim(1,ts,[i])]:=[i];
end for;
m:=0; for i in [1..15] do if cst[i] ne []
227
then m:=m+1; end if; end for; m;
-----------------------------------------------------
N0:=Stabiliser(N,7);
Orbits(N0);
#N0;
N0;
-----------------------------------------------------
ts[14] eq ts[7]ˆ-1;
ts[14] eq ts[7]
*
ts[7];
ts[7]
*
ts[14] eq ts[7]
*
ts[7]
*
ts[7];
-----------------------------------------------------
N01:=Stabiliser(N,[7,1]);
N01;
#N01;
SSS:={[7,1]};
SSS:=SSSˆN;
SSS;
#SSS;
Seqq:=Setseq(SSS);
Seqq;
for i in [1..#SSS] do
for n in IN do
if ts[7]
*
ts[1] eq
n
*
ts[Rep(Seqq[i])[1]]
*
ts[Rep(Seqq[i])[2]]
then print Rep(Seqq[i]); end if; end for; end for;
N01s:=N01;
for n in N do if 7ˆn eq 4 and 1ˆn eq 2 then
N01s:=sub<N|N01s,n>; end if; end for;
for n in N do if 7ˆn eq 5 and 1ˆn eq 3 then
N01s:=sub<N|N01s,n>; end if; end for;
for n in N do if 7ˆn eq 3 and 1ˆn eq 8 then
N01s:=sub<N|N01s,n>; end if; end for;
for n in N do if 7ˆn eq 9 and 1ˆn eq 7 then
N01s:=sub<N|N01s,n>; end if; end for;
for n in N do if 7ˆn eq 1 and 1ˆn eq 9 then
N01s:=sub<N|N01s,n>; end if; end for;
for n in N do if 7ˆn eq 11 and 1ˆn eq 12 then
N01s:=sub<N|N01s,n>; end if; end for;
for n in N do if 7ˆn eq 10 and 1ˆn eq 4 then
N01s:=sub<N|N01s,n>; end if; end for;
for n in N do if 7ˆn eq 12 and 1ˆn eq 14 then
N01s:=sub<N|N01s,n>; end if; end for;
for n in N do if 7ˆn eq 2 and 1ˆn eq 10 then
N01s:=sub<N|N01s,n>; end if; end for;
228
for n in N do if 7ˆn eq 8 and 1ˆn eq 5 then
N01s:=sub<N|N01s,n>; end if; end for;
for n in N do if 7ˆn eq 14 and 1ˆn eq 11 then
N01s:=sub<N|N01s,n>; end if; end for;
N01s; #N01s;
for n in IN do if n
*
ts[7]
*
ts[1] eq ts[4]
*
ts[2] then n;
end if; end for;
for n in IN do if n
*
ts[7]
*
ts[1] eq ts[5]
*
ts[3] then n;
end if; end for;
for n in IN do if n
*
ts[7]
*
ts[1] eq ts[3]
*
ts[8] then n;
end if; end for;
for n in IN do if n
*
ts[7]
*
ts[1] eq ts[9]
*
ts[7] then n;
end if; end for;
for n in IN do if n
*
ts[7]
*
ts[1] eq ts[1]
*
ts[9] then n;
end if; end for;
for n in IN do if n
*
ts[7]
*
ts[1] eq ts[11]
*
ts[12] then n;
end if; end for;
for n in IN do if n
*
ts[7]
*
ts[1] eq ts[10]
*
ts[4] then n;
end if; end for;
for n in IN do if n
*
ts[7]
*
ts[1] eq ts[12]
*
ts[14] then n;
end if; end for;
for n in IN do if n
*
ts[7]
*
ts[1] eq ts[2]
*
ts[10] then n;
end if; end for;
for n in IN do if n
*
ts[7]
*
ts[1] eq ts[8]
*
ts[5] then n;
end if; end for;
for n in IN do if n
*
ts[7]
*
ts[1] eq ts[14]
*
ts[11] then n;
end if; end for;
for i in [1..15] do i, cst[i]; end for;
/
*
n1= (2, 5, 8)(3, 7, 12)(4, 13, 14)(6, 11, 10),
thus by using i, cst[i], we convert n to be
n= (7,5,3)(14,12,10)(4,1,13)(11,8,6) and so on for the
rest permutations
n2=(2, 14, 8)(3, 10, 12)(4, 5, 9)(6, 7, 15) =
(7,13,3)(14,6,10)(4,5,2)(11,12,9)
n3=(2, 11, 12, 6)(3, 13, 8, 4)(5, 9, 7, 15)(10, 14) =
(7,8,10,11)(14,1,3,4)(5,2,12,9)(6,13)
n4=(2, 4, 7)(3, 6, 5)(8, 10, 13)(11, 12, 14) =
(7,4,12)(14,11,5)(3,6,1)(8,10,13)
n5=(4, 15, 10)(5, 11, 12)(6, 9, 14)(7, 13, 8) =
(4,9,6)(5,8,10)(11,2,13)(12,1,3)
n6=(2, 4, 8, 5, 9, 13, 14)(3, 6, 12, 7, 15, 11, 10) =
(7,4,3,5,2,1,13)(14,11,10,12,9,8,6)
n7=(2, 11, 4, 8)(3, 13, 6, 12)(5, 7)(9, 14, 15, 10) =
229
(7,8,4,3)(14,1,11,10)(5,12)(2,13,9,6)
n8=(4, 8, 9)(5, 14, 13)(6, 12, 15)(7, 10, 11) =
(4,3,2)(5,13,1)(11,10,9)(12,6,8)
n9=(2, 15, 10, 8, 4, 13, 7)(3, 9, 14, 12, 6, 11, 5) =
(7,9,6,3,4,1,12)(14,2,13,10,11,8,5)
n10=(2, 7, 10)(3, 5, 14)(4, 15, 8)(6, 9, 12) =
(7,12,6)(14,5,13)(4,9,3)(11,2,10)
n11=(2, 4, 13)(3, 6, 11)(5, 14, 9)(7, 10, 15) =
(7,4,1)(14,11,8)(5,13,2)(12,6,9)
*
/
for i in [1..168] do if ArrayP[i] eq
N!(7,5,3)(14,12,10)(4,1,13)(11,8,6) then Sch[i];
end if; end for;
for i in [1..168] do if ArrayP[i] eq
N!(7,13,3)(14,6,10)(4,5,2)(11,12,9) then Sch[i];
end if; end for;
for i in [1..168] do if ArrayP[i] eq
N!(7,8,10,11)(14,1,3,4)(5,2,12,9)(6,13) then Sch[i];
end if; end for;
for i in [1..168] do if ArrayP[i] eq
N!(7,4,12)(14,11,5)(3,6,1)(8,10,13) then Sch[i];
end if; end for;
for i in [1..168] do if ArrayP[i] eq
N!(4,9,6)(5,8,10)(11,2,13)(12,1,3) then Sch[i];
end if; end for;
for i in [1..168] do if ArrayP[i] eq
N!(7,4,3,5,2,1,13)(14,11,10,12,9,8,6)then Sch[i];
end if; end for;
for i in [1..168] do if ArrayP[i] eq
N!(7,8,4,3)(14,1,11,10)(5,12)(2,13,9,6) then Sch[i];
end if; end for;
for i in [1..168] do if ArrayP[i] eq
N!(4,3,2)(5,13,1)(11,10,9)(12,6,8) then Sch[i];
end if; end for;
for i in [1..168] do if ArrayP[i] eq
N!(7,9,6,3,4,1,12)(14,2,13,10,11,8,5)then Sch[i];
end if; end for;
for i in [1..168] do if ArrayP[i] eq
N!(7,12,6)(14,5,13)(4,9,3)(11,2,10) then Sch[i];
end if; end for;
for i in [1..168] do if ArrayP[i] eq
N!(7,4,1)(14,11,8)(5,13,2)(12,6,9) then Sch[i];
end if; end for;
230
f(y
*
x
*
y
*
x
*
yˆ-1
*
x
*
yˆ-1
*
x
*
yˆ-1)
*
ts[7]
*
ts[1] eq ts[4]
*
ts[2];
f(yˆ-1
*
x
*
y
*
x
*
y
*
x
*
yˆ-1
*
x
*
y)
*
ts[7]
*
ts[1] eq ts[5]
*
ts[3];
f(x
*
y
*
x
*
yˆ-1
*
x
*
yˆ-1)
*
ts[7]
*
ts[1] eq ts[3]
*
ts[8];
f(y
*
x
*
y
*
x
*
y
*
x
*
yˆ-1
*
x
*
yˆ-1
*
x)
*
ts[7]
*
ts[1] eq ts[9]
*
ts[7];
f(x
*
yˆ-1
*
x
*
yˆ-1
*
x
*
y
*
x)
*
ts[7]
*
ts[1] eq ts[1]
*
ts[9];
f(y
*
x
*
y
*
x
*
yˆ-1
*
x
*
yˆ-1
*
x
*
y)
*
ts[7]
*
ts[1] eq ts[11]
*
ts[12];
f(y
*
x
*
yˆ-1
*
x
*
yˆ-1
*
x)
*
ts[7]
*
ts[1] eq ts[10]
*
ts[4];
f(x
*
y
*
x
*
y
*
x
*
yˆ-1
*
x
*
yˆ-1)
*
ts[7]
*
ts[1] eq ts[12]
*
ts[14];
f(y
*
x
*
yˆ-1
*
x
*
yˆ-1
*
x
*
y)
*
ts[7]
*
ts[1] eq ts[2]
*
ts[10];
f(y
*
x
*
y
*
x
*
yˆ-1
*
x
*
y
*
x
*
y
*
x)
*
ts[7]
*
ts[1] eq ts[8]
*
ts[5];
f(x
*
y
*
x
*
y
*
x
*
yˆ-1
*
x)
*
ts[7]
*
ts[1] eq ts[14]
*
ts[11];
231
Appendix O: MAGMA Code for
Isomorphism Type of 3
7
: L
2
(7)
S:=Sym(14);
xx:=S!(1, 8)(3, 4)(5, 6)(7, 14)(10, 11)(12, 13);
yy:=S!(1, 2, 3)(4, 5, 7)(8, 9, 10)(11, 12, 14);
N:=sub<S|xx,yy>;
#N;
k:=0; l:=0; m:=0; n:=3; o:=4; p:=0;
G<x,y,t>:=Group<x,y,t|xˆ2,yˆ3,(x
*
y)ˆ7,(x,y)ˆ4, tˆ3,
tˆ(y
*
x
*
yˆ-1
*
x
*
y
*
x
*
y
*
x
*
yˆ-1
*
x
*
y)
*
tˆ-1,
tˆ(y
*
x
*
yˆ-1
*
x
*
y
*
x
*
yˆ-1)
*
tˆ-1,tˆx=tˆ-1,(x
*
y
*
t)ˆk,
(x
*
tˆy
*
tˆ2)ˆl,(xˆy
*
t)ˆm,(yˆx
*
tˆ2
*
t)ˆn,(yˆ2
*
(x
*
y)ˆ5
*
t)ˆo,
(x
*
yˆ-1
*
t)ˆp>;
f,G1,k:=CosetAction(G,sub<G|x,y>);
#G; #G1; #k;
CompositionFactors(G1);
#sub<G|x,y>;
#DoubleCosets(G,sub<G|x,y>,sub<G|x,y>);
Center(G1);
NL:=NormalLattice(G1);
NL;
MinimalNormalSubgroups(G1);
X:=AbelianGroup(GrpPerm,[3,3,3,3,3,3,3]);
s:=IsIsomorphic(X,NL[2]);
s;
D:=DirectProduct(NL[2],NL[3]);
s:=IsIsomorphic(NL[3],D);
s;
DD:=DerivedGroup(G1);
DD;
IsPerfect(DD);
232
DB:=PerfectGroupDatabase();
PermutationGroup(DB,367416,1);
s:=IsIsomorphic(PermutationGroup(DB,367416,1),G1);
s;
PermutationGroup(DB,367416,2);
s:=IsIsomorphic(PermutationGroup(DB,367416,2),G1);
s;
Group(DB,367416,2);
H<a,b,t,u,v,x,y,w,z>:=Group<a,b,t,u,v,x,y,w,z|aˆ2,
bˆ3,(a
*
b)ˆ7,(a,b)ˆ4,tˆ3,uˆ3,vˆ3,xˆ3,yˆ3,wˆ3, zˆ3,(a,tˆ-1),
(t,u),(t,v),(t,w),(t,x),(t,y),(t,z),(u,v),(u,w),(u,x),
(u,y),(u,z),(v,w),(v,x),(v,y),(v,z),(w,x),(w,y),(w,z),
(x,y), (x,z),(y,z),(a,tˆ-1),aˆ-1
*
u
*
a
*
wˆ-1,aˆ-1
*
v
*
a
*
v,
aˆ-1
*
w
*
a
*
uˆ-1,aˆ-1
*
x
*
a
*
zˆ-1,aˆ-1
*
y
*
a
*
y,aˆ-1
*
z
*
a
*
xˆ-1,
bˆ-1
*
t
*
b
*
uˆ-1,bˆ-1
*
u
*
b
*
vˆ-1,bˆ-1
*
v
*
b
*
tˆ-1,bˆ-1
*
w
*
b
*
xˆ-1,
bˆ-1
*
x
*
b
*
yˆ-1,bˆ-1
*
y
*
b
*
wˆ-1,(b,zˆ-1)>;
f,H1,k:=CosetAction(H,sub<H|Id(H)>);
#H;
s:=IsIsomorphic(H1,G1);
s;
233
Appendix P: MAGMA Code for
Universal Cover of A
6
S:=Sym(432);
a:=S!(1,2,8,5)(3,13,22,16)(4,10,9,19)(6,7,12,18)
(11,25,20,26)(14,31,21,32)(15,28,23,35)(17,30,34,38)
(24,39,33,40)(27,45,36,48)(29,51,37,52)(41,67,43,69)
(42,70,44,71)(46,77,53,79)(47,74,59,81)(49,76,61,84)
(50,85,60,86)(54,90,62,93)(55,95,57,97)(56,73,58,82)
(63,99,65,101)(64,102,66,103)(68,107,72,108)
(75,115,83,116)(78,120,87,123)(80,122,94,126)
(88,133,91,135)(89,105,92,109)(96,143,98,144)
(100,149,104,150)(106,156,110,157)(111,163,112,164)
(113,165,117,166)(114,167,127,168)(118,171,128,174)
(119,175,124,177)(121,179,125,180)(129,183,131,185)
(130,147,132,151)(134,190,137,191)(136,189,139,195)
(138,141,140,145)(142,198,146,199)(148,194,152,188)
(153,203,154,204)(155,205,158,206)(159,209,161,210)
(160,211,162,212)(169,225,172,227)(170,229,173,230)
(176,236,181,238)(178,241,182,242)(184,248,186,249)
(187,251,193,253)(192,258,196,261)(197,263,200,264)
(201,267,202,268)(207,245,208,243)(213,283,215,285)
(214,286,216,287)(217,240,219,237)(218,290,220,291)
(221,293,223,295)(222,281,224,279)(226,299,231,300
)(228,298,233,303)(232,235,234,239)(244,250,246,247)
(252,311,255,309)(254,312,262,310)(256,276,259,274)
(257,323,260,324)(265,277,266,278)(269,280,271,282)
(270,338,272,339)(273,341,275,343)(284,347,288,348)
(289,321,292,325)(294,342,296,344)(297,355,302,356)
(301,358,306,359)(304,361,305,362)(307,363,308,364)
(313,367,314,368)(315,336,317,334)(316,369,318,370)
(319,371,320,372)(322,332,327,330)(326,376,328,379)
(329,381,331,382)(333,375,335,378)(337,380,340,373)
234
(345,385,346,386)(349,357,350,360)(351,354,352,353)
(365,395,366,396)(374,407,377,409)(383,391,384,393)
(387,408,389,411)(388,410,390,412)(392,402,394,401)
(397,398,399,400)(403,404,405,406)(413,415,414,416)
(417,431,418,432)(419,425,420,426)(421,422,423,424)
(427,430,428,429);
b:=S!(1,3,14,12,8,22,21,6)(2,9,23,20,5,4,15,11)
(7,17,33,19,18,34,24,10)(13,27,46,37,16,36,53,29)
(25,41,68,44,26,43,72,42)(28,47,78,60,35,59,87,50)
(30,49,80,62,38,61,94,54)(31,55,96,58,32,57,98,56)
(39,63,100,66,40,65,104,64)(45,73,113,83,48,82,117,
75)(51,88,134,92,52,91,137,89)(67,105,155,110,69,
109,158,106)(70,111,127,81,71,112,114,74)(76,103,
154,128,84,102,153,118)(77,119,149,125,79,124,150,
121)(85,129,184,132,86,131,186,130)(90,136,192,140,
93,139,196,138)(95,141,197,146,97,145,200,142)(99,
147,201,152,101,151,202,148)(107,159,126,162,108,
161,122,160)(115,169,226,173,116,172,231,170)(120,
176,144,182,123,181,143,178)(133,187,252,194,135,
193,255,188)(156,195,262,208,157,189,254,207)(163,
213,284,216,164,215,288,214)(165,217,289,220,166,
219,292,218)(167,221,294,224,168,223,296,222)(171,
228,301,234,174,233,306,232)(175,235,307,240,177,
239,308,237)(179,243,313,246,180,245,314,244)(183,
247,266,199,185,250,265,198)(190,256,321,260,191,
259,325,257)(203,269,337,272,204,271,340,270)(205,
273,342,276,206,275,344,274)(209,277,319,251,210,
278,320,253)(211,279,345,282,212,281,346,280)(225,
297,351,290,227,302,352,291)(229,304,283,238,230,
305,285,236)(241,309,365,312,242,311,366,310)(248,
315,347,318,249,317,348,316)(258,322,373,328,261,
327,380,326)(263,329,299,332,264,331,300,330)(267,
333,359,336,268,335,358,334)(286,295,354,350,287,
293,353,349)(298,357,355,339,303,360,356,338)(323,
374,408,378,324,377,411,375)(341,376,410,384,343,
379,412,383)(361,387,417,390,362,389,418,388)(363,
391,419,394,364,393,420,392)(367,397,425,400,368,
399,426,398)(369,401,413,381,370,402,414,382)(371,
403,427,406,372,405,428,404)(385,415,430,409,386,
416,429,407)(395,421,431,424,396,423,432,422);
G:=sub<S|a,b>;
C:=Center(G);C;
235
Order(C.1);
Order(C.2);
Order(C.2ˆ3);
Order(C.1
*
C.2);
Order(C.1
*
C.2ˆ2);
c:=C.2;
Order(c);
Order(cˆ2);
Order(cˆ3);
q,ff:=quo<G|cˆ3>;
q;
CompositionFactors(q);
S:=Sym(18);
a:=S!(2,6)(4,11)(7,9)(8,13)(10,14)(12,16);
b:=S!(1,2,7,4)(3,8,6,10)(5,9,13,12)(11,15)(14,17)(16,18);
G1:=sub<S|a,b>;
s:=IsIsomorphic(q,G1);
s;
D:=Center(G1);D;
qq,fff:=quo<G1|D>;
qq;
CompositionFactors(qq);
s:=IsIsomorphic(qq,Alt(6));
s;
236
Bibliography
[CB] J. Cannon and W. Bosma. Handbook of magma functions.
https://www.google.com/?gws_rd=sslq=handbook+of+magma+
functions+volume+3+infinite+groups.
[Cur07] R.T. Curtis. Symmetric Generation of Groups: With Applications to many of
the Sporadic Simple Finite Groups. Cambridge University Press, 2007.
[DM96] John D. Dixon and B. Mortimer. Permutation Groups. Springer, 1996.
[Isa76] M. Isaacs. Character Theory of Finite Groups. Dover Publication, 1976.
[Rot95] Joseph J Rotman. An Introduction to the Theory of Groups. Springer, 1995.
[Tra13] Jesse Graham Train. Enumeration and symmetric presentations of groups,
with music theory applications. Master’s thesis, CSUSB, June 2013.
[Why06] Sophie Whyte. Symmetric Generation: Permutation Images and Irreducible
Monomial Representations. PhD thesis, University of Birmingham, September
2006.
[Wik] Wikipedia. Schur multiplier. http://en.wikipedia.org/wiki/Schur_
multiplier.
[WWI] R Wilson, P Walsh, and Suleiman I. Atlas of finite group representations -
version 3. http://brauer.maths.qmul.ac.uk/Atlas/v3/.
